Identifikace postupujících vln v signálu snímače napětí ve vysokonapěťové síti pomocí metody krátkodobé maticové tužky

V testech byl použit vektorový obvodový analyzátor Omicron-Lab Bode 100 od společnosti DACPOL SP. Z O.O.

Abstrakce

Většina metod lokalizace poruchových vln je založena na analýze proudu ve vedení transformovaného proudovými transformátory a je omezena na vysokonapěťové sítě. Lokalizace poruchových vln v sítích vysokého napětí se stále vyvíjí. Tento článek představuje nový algoritmus v reálném čase pro identifikaci postupujících vln v distribuční síti pomocí napěťového signálu a metody krátkodobé maticové tužky. Pro získání průběhů napětí na sekundární straně rozvodny byl vyvinut model odporového napěťového senzoru založený na širokopásmových měřeních od 10 Hz do 20 MHz. Testovaný senzor zesiluje frekvence spojené s postupujícími vlnami více než je užitná frekvence, což umožňuje identifikaci. Pro testování algoritmu byly provedeny simulace zkratu na IEEE 34-bus feeder. Vyvinutá metoda dokáže detekovat i vlny s nízkou amplitudou.

1. Úvod

Ochrana energetického systému před poruchami je jedním z cílů ochranného relé. Rychlé odstranění rušení omezuje škody způsobené na energetických zařízeních a snižuje jejich negativní dopad na kvalitu elektrické energie. Proto je vývoj rychlých a přesných relé a lokalizátorů poruch v distribučních sítích klíčovou otázkou jak z technického, tak ekonomického hlediska. V případě sítí vysokého napětí je lokalizace poruch snadná, protože se vyznačují velkým rozptylem měření a strukturou smyčky. V případě distribučních sítí se měření provádí převážně na jednom místě tamní rozvodny. Distribuční sítě mají navíc stromovou strukturu, což činí identifikaci vadné větve nejistou. Řešením tohoto problému může být použití lokátorů postupných vln, které v tomto případě mohou být přesnější než konvenční metody. Aby bylo použití takových lokátorů možné, je nutné vyvinout co nejpřesnější metody identifikace postupné vlny.

Konvenční přístup k detekci poruch je založen na analýze proudů a napětí základní frekvence. Z tohoto důvodu ochranné algoritmy založené na těchto typech signálů vyžadují analýzu signálového intervalu, který je dostatečně dlouhý, aby se ujistil, že k rušení došlo. Modernější přístup je založen na postupných vlnách, což jsou signály s vyšší frekvencí šířící se podél elektrického vedení. Tento typ ochrany se někdy nazývá „ultra-vysokorychlostní“. Detekuje proudové a napěťové vlny generované poruchami. Tato ochrana pak na základě porovnání jejich amplitud a časů příchodu do měřicích zařízení určí jak druh, tak i místo rušení. Klíčovou výhodou vlnové ochrany je bezesporu rychlost provozu (méně než 4 ms) [1]. Navíc správně funguje se sériově kompenzovanými přenosovými vedeními a při výkyvech výkonu.

Umístění poruchy pomocí postupných vln lze rozdělit na dvousvorková a jednosvorková schémata. V případě dvousvorkových relé dochází ke sběru naměřených dat na koncích chráněných vedení a vyžaduje přenos naměřených dat mezi zařízeními. Jednosvorková relé však analyzují signály proudů a napětí pouze z jednoho měřicího bodu. Je třeba zdůraznit, že dvousvorková relé se vyznačují vyšší spolehlivostí, protože k lokalizaci a klasifikaci využívají vlny přímo generované poruchou. Tyto vlny mají nejvyšší možnou amplitudu a jsou detekovány jako první po poruše. V případě jednosvorkových relé je však ochrana založena na vlně generované poruchou a na vlnách odražených od přerušení vedení, větví a samotné poruchy [2]. Je to kvůli chybějícímu druhému měřicímu bodu v síti.

Sítě vysokého napětí se vyznačují přítomností rozvoden s měřicím zařízením na koncích vedení. Zde se proto používají dvousvorková relé. V případě distribučních sítí jsou rozvodny vysokého/středního napětí obvykle jediným místem, kde jsou umístěna ochranná relé s transformátory nebo snímači. To znamená, že v distribučních sítích je použití jednokoncových vlnových relé nejlevnějším řešením.

Distribuční sítě jsou sítě se stromovou topologií a tato funkce ztěžuje přesnou lokalizaci poruchy. U konvenčních i vlnových lokátorů poruch je situace složitější než u přenosových sítí, protože ve známé vzdálenosti od rozvodny může existovat několik potenciálních poruchových větví. Pouze jedna z větví je vadná. Zkratované vedení však lze určit porovnáním amplitud proudových vln rozptýlených na sběrnicích rozvodny [2,3,4].

Byly navrženy různé metody lokalizace poruch, jako je detekce frekvencí spojených s oscilacemi vln mezi uzly [5], porovnání naměřeného proudu s předpokládaným proudem pro dané místo zkratu [6] a tradičnější metody založené na detekci čel zlomových vln [3,7]. K detekci vlnoploch byly použity následující metody: vlnková transformace, analýza hlavních složek založená na extrakci příznaků, Teagerův energetický operátor, souborová empirická dekompozice módů a metoda maticové tužky, která je diskutována a používána v tomto článku [8,9]. Metoda maticové tužky se používá k rozložení signálu na součet exponenciálně tlumených sinusoid [10]. V oblasti elektroenergetiky se metoda maticové tužky používá k odhadu základních módů kmitání v důsledku poruch a k odhadu harmonických a subharmonických [11,12,13].

Elektrické signály zpracované algoritmy digitálního zpracování dat jsou do ochrany dodávány pomocí měřicích zařízení umístěných na stanici. Mezi tato zařízení patří proudové a napěťové transformátory, Rogowského cívky nebo senzory snižující úroveň elektrických signálů na úroveň přijatelnou pro relé. Je důležité, aby signál na sekundární straně těchto zařízení byl reprodukován co nejpřesněji a v ideálním případě by měl být pouze škálován. V praxi však mají měřicí přístroje proměnný zisk a fázový posun v závislosti na frekvenci signálu. Vysoké frekvence by neměly být přístrojem příliš tlumeny, aby bylo možné detekovat příchozí postupnou vlnu, která je rychle se měnícím průběhem a obsahuje tedy vysokofrekvenční složky. Je třeba zdůraznit, že pro přesnou reprodukci amplitudy poruchové vlny by měl přístroj zavést konstantní časové zpoždění (nejlépe žádné) a jeho zesilovací charakteristiky by měly být co nejméně proměnlivé.

Transformátory jsou přístroje, které se tradičně používají v elektroenergetice k měření napětí. Vyznačují se velmi přesnou transformací elektrických signálů, ale mají i nevýhody. Přispívají k negativnímu jevu ferorezonance, jsou vystaveny škodám způsobeným zkraty v sekundárním obvodu a nejsou schopny přesně transformovat vysokofrekvenční (>3 kHz) složky napětí [14]. Proto byly vyvinuty nekonvenční snímače založené na mechanismech odlišných od transformátorového systému jako reakce na potřebu přesně měřit přechodové složky [15,16].

Pro měření napětí jsou oblíbenými nekonvenčními senzory napěťové senzory založené na kapacitních (C), odporových (R) a odporově-kapacitních (RC) děličích [14]. Zejména děliče R a RC jsou nejoblíbenější, protože nejsou schopny indukovat ferorezonanci kvůli zanedbatelné indukčnosti, přesně transformují přechodové jevy a vysoké frekvence, umožňují vybíjení nahromaděného náboje na vedení a jsou odolné vůči zkratům na sekundární straně. Tyto děliče lze úspěšně použít pro měření kvality elektrické energie a pro lokalizaci zkratu pomocí vlnových jevů.

Literatura o modelování konvenčních transformátorů je rozsáhlá, ale bohužel obvykle odkazuje na popis jejich charakteristik při frekvencích pod 10 kHz [15,17]. Číselné údaje Bodeových grafů či přenosových funkcí napěťových transformátorů (klasických i nekonvenčních) do 1 MHz se autorům navíc nepodařilo najít ani v článcích popisujících studie v této oblasti [18,19]. Taková data jsou k dispozici pro konvenční proudový transformátor [20]. Senzory se samozřejmě liší v konstrukci, což vede k odchylkám jejich přenosových charakteristik od jednoho typu k druhému, ale znalost přenosové funkce příkladu se zdá být potřeba.

Za účelem získání takových dat byla provedena měření frekvenčních charakteristik vysokonapěťového senzoru. Poté byly použity k vytvoření modelu přenosové funkce. Vylepšená metoda krátkodobé maticové tužky byla následně představena v aplikaci pro detekci napěťových zkratových vln ve vysokonapěťové síti měřených na sekundární straně napěťových senzorů.

Struktura papíru je následující. Část 2 popisuje krátkodobou maticovou tužkovou metodu s její aplikací pro vyhledávání signálových impulsů. Je zde také poskytnut algoritmus pro identifikaci pulsů. Sekce 3 obsahuje výsledky měření přenosové funkce snímače napětí a výsledky činnosti algoritmu na základě provedených simulací. Závěry jsou uvedeny v části 4.

2. Identifikace poruchových impulsů ve vysokonapěťové síti

2.1. Krátkodobá maticová tužková metoda

Metoda krátkodobé maticové tužky (STPMM) aproximuje signál uvnitř okna, který se pohybuje s časem jako součet sinusových složek s exponenciálně proměnnou amplitudou [10,21]:

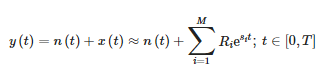
kde:

• y(t) – signál měření,
• n(t) – hluk,
• x(t) – původní signál,
• Ri – rezidua nebo komplexní amplitudy komponent,
• Si – komplexní póly a
• M – počet aproximačních složek.

Pro vzorkovaný signál t = kT_s má výše uvedená rovnice následující tvar:

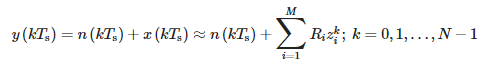
kde:

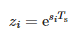
• Ts – období vzorkování a
• N – počet vzorků.

Aby bylo možné určit aproximační parametry, sestaví se následující matice:

Zde L je parametr tužky. Počet aproximačních složek M splňuje následující vztah:

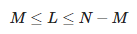
Vidíme tedy, že maximální hodnota M je rovna ⌊N/2⌋.
Vystavením matice Y rozkladu singulární hodnoty (SVD) získáme:

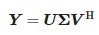
kde:

• U – jednotková matice velikosti (N − L) × (N − L),
• Σ – obdélníková diagonální matice singulárních hodnot o velikosti (N − L) × (L + 1) a
• V – jednotková matice velikosti (L + 1) × (L + 1).

Pokud by měřený signál neobsahoval žádný šum, matice Σ by obsahovala přesně M nenulové singulární hodnoty. Vlivem šumu mohou být singulární hodnoty zkresleny, což se projevuje dodatečnými malými singulárními hodnotami. Šumový efekt je eliminován odstraněním těchto malých hodnot. Zbývá pouze M dominantních hodnot, které splňují následující podmínku:

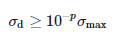
kde σ_max je dominantní singulární hodnota a p je počet přesných platných desetinných míst měření.

Potom se zkonstruují podmatice výsledných matic SVD:

1. Matice U′=[u1,u2,…,u_M] velikosti (N − L) × M se vytvoří ponecháním sloupců odpovídajících singulárním hodnotám splňujícím podmínku (7) a odstraněním ostatní;
2. Čtvercová diagonální matice Σ=diag(σ1,σ2,…,σM) je vytvořena odstraněním sloupců a řádků matice Σ, které obsahují singulární hodnoty, které nesplňují podmínku (7);
3. Matice V′=[v1,v2,…,v_M] velikosti (L + 1) × M se vytvoří ponecháním sloupců odpovídajících singulárním hodnotám splňujícím podmínku (7) a odstranění ostatních.

Poté se vytvoří matice V₁′ odstraněním posledního řádku matice V′. V₂′ se vytváří odstraněním prvního řádku matice V′.

Potom se vypočítají následující matice:

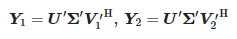
Hodnoty zi jsou nenulové zobecněné vlastní hodnoty páru matic (Y₁, Y₂), konkrétně vlastní hodnoty Y ^†₁Y₂, kde Y^†₁ je Moore-Penrose pseudoinverze k Y₁. Pak vypočítáme póly:

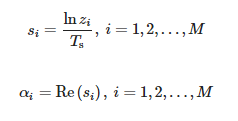
Hodnoty amplitud lze určit následovně:

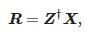
kde:

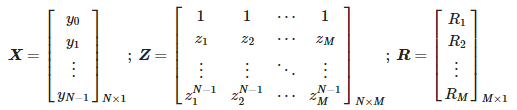
Výše uvedené operace se provádějí metodou krátkodobé maticové tužky pro po sobě jdoucí intervaly dat [9,22].

Přibližné výsledky vlastních čísel, pseudoinverzí a SVD algoritmů mohou ovlivnit vznik zi nenulových, i když se blíží nulovým hodnotám. Tyto hodnoty ovlivňují rychlost MPM a mohou nepříznivě ovlivnit jejich výsledky, proto se vyplatí je před výpočtem zbytků odstranit.

2.2. Chování komponentních pólů v okolí pulsu

Poruchy v elektrické síti generují impulsy šířící se podél elektrického vedení rychlostí blízkou rychlosti světla [3]. Tyto impulsy lze identifikovat pomocí analýzy pólového posunu aproximace STMPM. Obrázek 1 ukazuje tři příklady pulzů Gaussova tvaru a póly jejich aproximace pomocí STMPM. Když přijde puls, aproximace s exponenciálními složkami se mění s pohybem časového okna. Když je puls napravo od středního bodu okna, póly aproximace mají kladnou reálnou část, když je Gaussův vrchol uprostřed okna, skutečná část pólů je blízká nule a když puls je v první polovině okna, póly mají zápornou reálnou část. Změna znaménka skutečné části pólů tedy naznačuje, že střed pulzu prošel středním bodem vzorkovacího okna [9,22]. Z obrázku 2 také vidíme, že póly s největší absolutní hodnotou skutečné součásti (a tedy s nejrychlejší rychlostí změny amplitudy) mají největší hodnotu počátečního modulu amplitudy (rezidua).

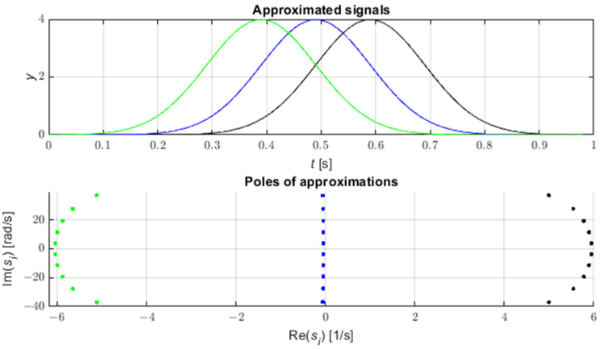
Obrázek 1. Gaussovy a odpovídající póly aproximace.

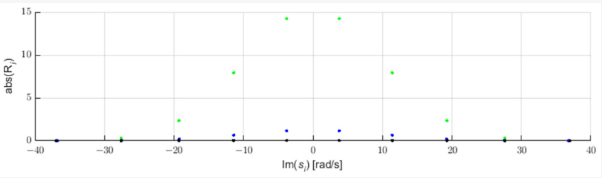
Obrázek 2. Zbytky složek Gaussových aproximací.

Vidíme tedy, že časovou souřadnici vrcholu impulsu lze přibližně ztotožnit s okamžikem změny znaménka koeficientů tlumení.

Získáním časově závislého průběhu těchto koeficientů pomocí STMPM je můžeme podrobit lineární aproximaci v blízkosti bodu, kde koeficienty procházejí nulou a získat přibližnou vrcholovou souřadnici pulzu. Je třeba poznamenat, že koeficienty charakterizované nejvyšší variabilitou jsou také charakterizovány nejvyšší amplitudou – jsou největšími složkami pulzu.

2.3. Algoritmus detekce pulzu v reálném čase

Vývojový diagram algoritmu pro detekci impulsů pocházejících z postupujících vln je uveden na obrázku 3. Algoritmus podrobuje postupná okna signálu STMPM, aby se extrahovaly rychlosti rozpadu aproximačních složek.

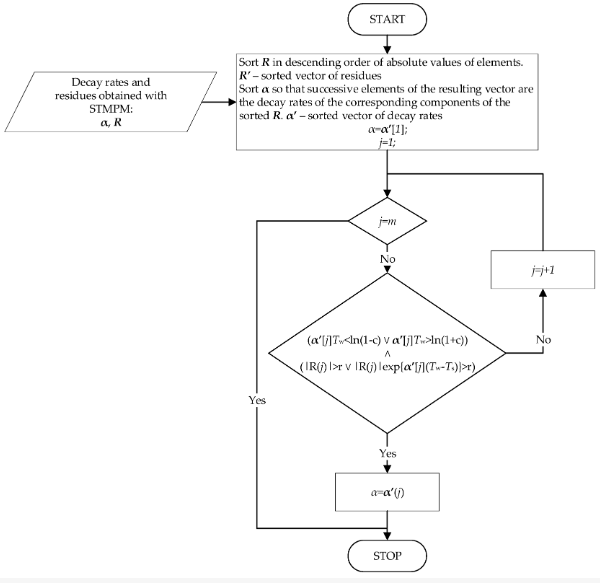
Obrázek 3. Algoritmus výběru rychlostí rozpadu.

Získané komponenty jsou podrobeny selekci, jejíž postup je znázorněn na obrázku 4. Výběr je založen na předpokladu, že ty komponenty STMPM, které se vyznačují největší amplitudou, by měly být brány za dobu špičky. aproximace – představují největší příspěvek k přechodné složce signálu. To je v souladu s pozorováním z předchozího bodu – složky s největší variací amplitudy jsou charakterizovány největší počáteční amplitudou. V případě, kdy je složka s největší amplitudou charakterizována malou rychlostí doznívání během celého okna délky T_w – menší než parametr c – nebo je její maximální příspěvek k signálu menší než r, další složka z hlediska velikosti amplitudy je vybrána jako potenciální kandidát na rychlost rozpadu α. Opakováním tohoto postupu pro následující složky, dokud není podmínka splněna, se nakonec získá koeficient α, který se pak použije k aproximaci doby příchodu impulsu. Pokud žádná ze složek nesplňuje výše uvedené podmínky, je vybrána ta s nejvyšší amplitudou.

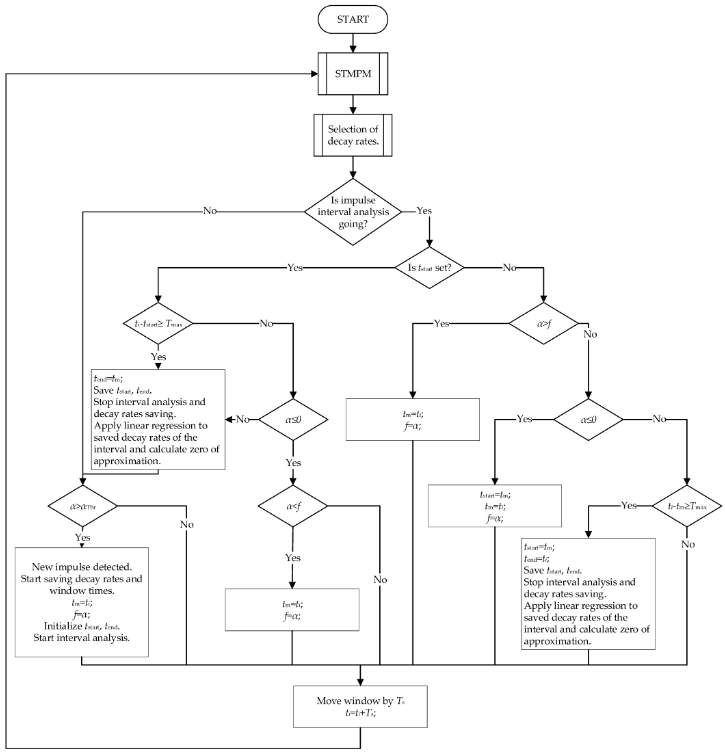
Obrázek 4. Algoritmus identifikace pulzu.

Čas spojený s oknem je považován za:

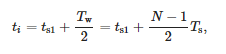
kde t_s1 – čas prvního vzorku okna a T_w – šířka okna.

Příchod pulzu je indikován prudkým zvýšením rychlostí α spojeným s rychlou změnou signálu na konci vzorkovacího okna. Parametr α_Thr je vybrán jako práh rychlosti poklesu. Když je překročen práh detekce, následné hodnoty koeficientů α a časů okna se zapíší do paměti a spustí se analýza dat pro určení přesnějších hranic impulzů. Jako správný začátek pulzu je zvolen okamžik t_start s nejvyšší hodnotou α před změnou znaménka rychlosti doznívání. Pro uložení potenciálních časů správných hranic impulsů byla zavedena proměnná t_m s proměnnou f obsahující dosud největší hodnoty α impulsu.

Pokud je nalezena hodnota t_start, spustí se hledání konečného správného konce t_end pulzu. To odpovídá nejmenší hodnotě α, než se znaménko znovu změní, tentokrát na kladné. Proměnná i_m se opět používá k uložení předchozích potenciálních koncových bodů. Proměnná f obsahuje předchozí minimální hodnoty α.

Když je délka pulzu rovna T_max vzorků nebo je nalezen konec pulzu, analýza pulzu je ukončena.

Funkce α(t) v intervalu [t_start; t_end] je podroben lineární regresi. Koeficienty této regrese byly nalezeny jako řešení následujícího problému:

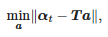
kde: α_t=[α(t_start),α(t_start+Ts),…,α(t_end)]^T, a=[a₁,a₀]^T

Hledané koeficienty jsou:

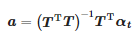
Vzhledem k tomu, že okamžik příchodu impulsu je:

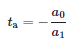
2.4. Upravený testovací podavač IEEE 34-Bus

Pro výpočty zkratů byl vytvořen 34sběrnicový testovací napájecí model IEEE v Simulinku. Topologie podavače je znázorněna na obrázku 5 [23]. Přivaděč je založen na reálné síti ve státě Arizona. Je dostatečně jednoduchý, aby se nestal podstatnou výpočetní zátěží během přechodových simulací s malým integračním krokem. Model byl zjednodušen a parametry byly změněny tak, aby napodobovaly evropské sítě:

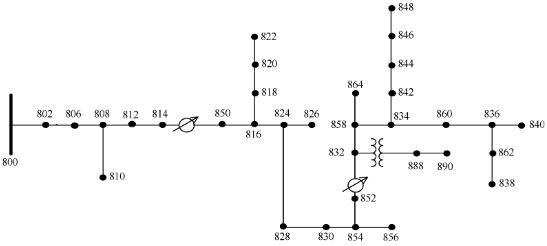
Obrázek 5. Topologie podavače sběrnice IEEE 34.

• Napětí sítě bylo změněno z 24,9 kV na 16,5 kV;
• Všechny úseky elektrického vedení byly považovány za nadzemní vedení se stejnými parametry;
• Byly odstraněny regulátory napětí;
• Předpokládalo se, že distribuovaná zátěž bude soustředěna na autobusy na vzdáleném konci naložených linek;
• Zátěže byly připojeny k síti vysokého napětí prostřednictvím distribučních transformátorů;
• Nulový bod transformátoru vysokého/středního napětí byl odpojen od uzemnění.

Parametry zdroje napětí:

• frekvence 50 Hz;
• síťové napětí 115,5 kV;
• Odpor 0,00227 Ω.
• Symetrický zdroj s fázovým posunem fáze L1 rovným 0°.

Parametry napájecího transformátoru:

• Poměr napětí 115,5/16,5;
• Vektorová skupina vysokonapěťového vinutí Yg;
• Vektorová skupina nízkonapěťového vinutí D11;
• Výkon 6,3 MVA;
• Relativní zkratové napětí 7,5 %;
• Odpor proti zkratu rovný 0,49 % ekvivalentní impedance.

Parametry distribučních transformátorů:

• Poměr napětí 15,75/0,4;
• Vektorová skupina vysokonapěťového vinutí D11;
• Vektorová skupina nízkonapěťového vinutí Yg;
• Výkon 630 kVA;
• Relativní zkratové napětí 6 %;
• Odpor proti zkratu rovný 17,2 % ekvivalentní impedance.

Parametry elektrického vedení:

• Třífázové vedení bez nulového vodiče;
• Jeden vodič na fázi;
• Průměr vodiče 0,8466 cm;
• T/D poměr 0,311;
• stejnosměrný odpor 0,5939 Ω/km;
• Vodorovné polohy vodičů x=[−1,05, 0, 1,05];
• Vertikální polohy vodičů u=[−9,05, 10,61, 9,05];
• Odpor uzemnění ρ=100 Ωm.

Kapacity byly připojeny ke každému transformátoru, jak je znázorněno na obrázku 6 [5] aby bylo možné modelovat vlastnosti transformátorů při vysokých frekvencích.

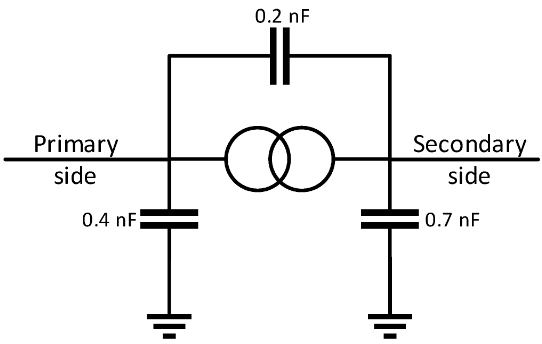
Obrázek 6. Model transformátoru.

Síťové linky byly modelovány mezi 1 Hz až 1 MHz s ohledem na efekt kůže pomocí modelu Universal Line Model.

Simulace jednofázových a vícefázových zkratů s nulovým přechodovým odporem byly provedeny při 20%, 50%, 80% a 100% délce vedení. Odpovídá 76 zkratovým místům. Integrační krok simulace byl Δt=0,1 μs. Použitou metodou integrace byl Tustin/Backward Euler.

3. Výsledky

3.1. Měření přenosových charakteristik vysokonapěťového senzoru

Měření frekvenční odezvy bylo provedeno pro vysokonapěťový snímač určený pro montáž do konektorových hlav. Snímač byl odporový dělič se jmenovitým primárním napětím 20/√3 kV a jmenovitým sekundárním napětím 3,25/√3, což odpovídá poměru napětí:

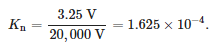
Pro měření byl použit vektorový síťový analyzátor Bode 100 společnosti OMICRON Lab. Toto zařízení umožňuje měření v rozsahu od 1 Hz do 50 MHz. K provedení testů byla použita funkce měření zisku a fáze zařízení. Tato funkce byla založena na porovnání amplitudy a fáze napěťových signálů na primární a sekundární straně snímače. Měření přenosové funkce definované jako poměr napětí na sekundární straně k napětí na primární straně bylo provedeno pro 2048 frekvenčních hodnot v rozsahu od 10 Hz do 20 MHz. Naměřené hodnoty jsou uvedeny na obrázku 7.

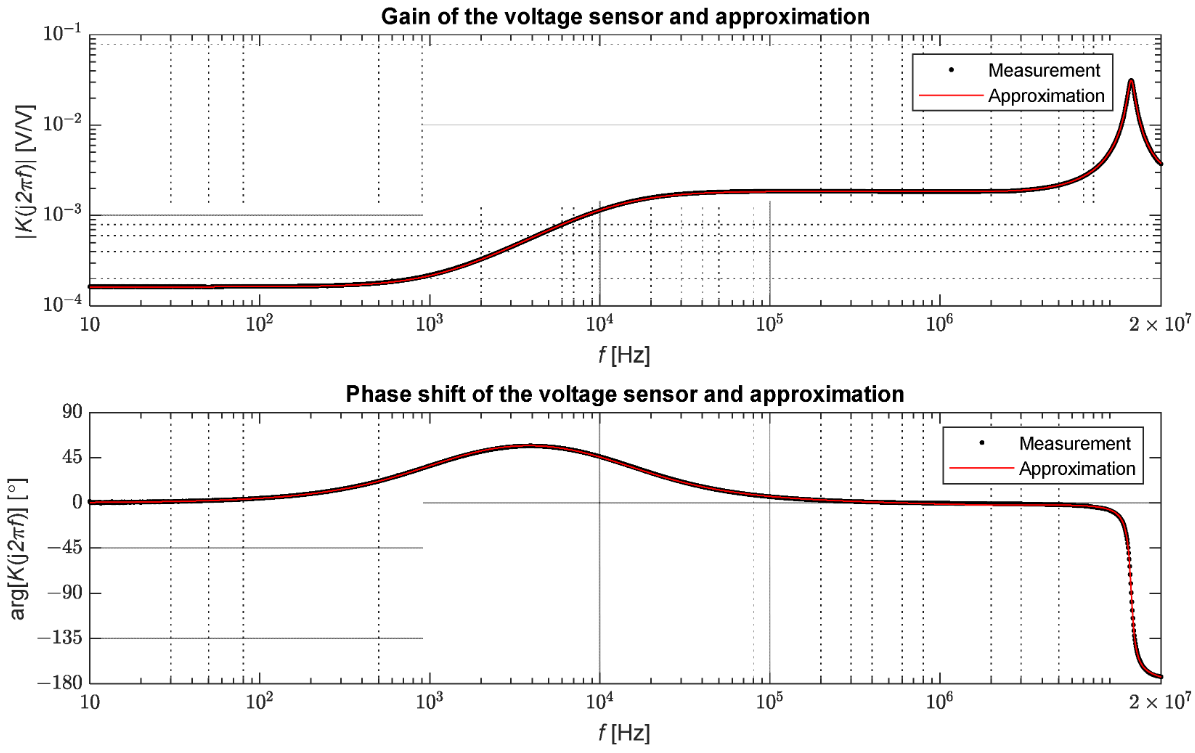
Obrázek 7. Výsledky měření propustnosti vysokonapěťového senzoru.

Testovaný napěťový senzor zachovává nominální koeficient přenosu pro signály do frekvence asi 1 kHz, poté graf stoupá na úroveň zesílení asi 1,84 × 10⁻³; tato úroveň je udržována mezi asi 12,5 kHz až 6,6 MHz. Díky diferenciační vlastnosti snímače je zde kladný fázový posun cca 57° v přechodové zóně od 100 Hz do 100 kHz. V případě fáze můžeme rozlišit dvě zóny, u kterých posun nepřesahuje 6°. V tomto případě je frekvenční rozsah přibližně do 130 Hz a od 105 kHz do 9,4 MHz. Lze tedy usoudit, že v rozsahu od 105 kHz do 6,6 MHz jsou signály proporcionálně transformovány, ale s jiným faktorem proporcionality než v blízkosti frekvence sítě. V případě vlnových jevů je tento rozsah dostatečný k přesnému zobrazení tvaru vln šířících se v mřížce [20]. Stojí za zmínku, že napěťové senzory s různou konstrukcí mohou vykazovat různé přenosové vlastnosti.

Pro vývoj matematického modelu senzoru byla použita funkce „tfest“ MATLABu k aproximaci dat získaných stabilní přenosovou funkcí následujícího tvaru:

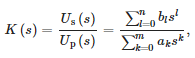
kde:

• Up(s) – napětí na primární straně senzoru,
• Us(s) – napětí na sekundární straně senzoru,
• n – pořadí čitatele,
• m – pořadí jmenovatele a
• ak, bl —koeficienty polynomů jmenovatele a čitatele propustnosti postupně.

Hodnoty koeficientů přenosové funkce jsou uvedeny v tabulce 1. Stojí za zmínku, že modelovaná propustnost je správná, protože řád jmenovatele je větší než řád čitatele. Obrázek 7 také uvádí srovnání přenosových funkcí získaných z měření s aproximací podle vzorce (19). Byla také vypočtena střední kvadratická chyba mezi body měření a aproximace určená následujícím vztahem:

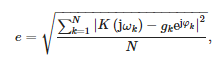
kde:

• N = 2048 – počet frekvencí měření
• g_k – měřené zesílení senzoru při pulzaci ω_k a
• φ_k —měřený fázový posun snímače při pulzaci ω_k.

Hodnota chyby aproximace je rovna:

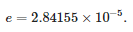
Tabulka 1. Hodnoty polynomických koeficientů ekvivalentní propustnosti napěťového senzoru s odporovou strukturou děliče.

Obrázek 8 ukazuje srovnání průběhu fázového napětí v rozvodně získaného ze simulace a napětí na výstupu modelovaného senzoru v případě přímého třífázového zkratu se zemí v uzlu 816. jasně viditelné, že zesílení rychlých přechodných jevů je větší než pomalých přechodných jevů. Stojí za zmínku, že tyto průběhy jsou zesíleny téměř proporcionálně.

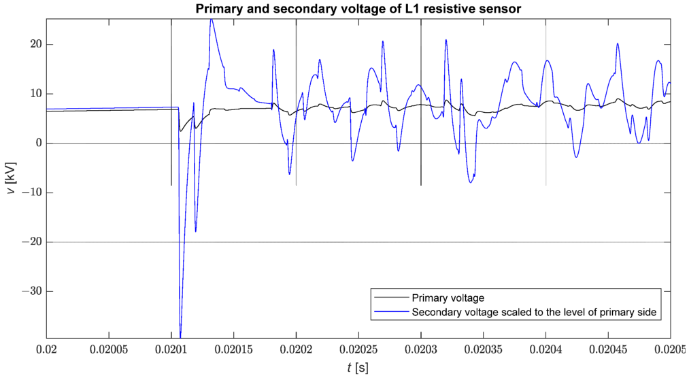
Obrázek 8. Porovnání průběhu fázového napětí (v_L1) a napětí na výstupu senzoru v měřítku primárního napětí (v_L1/K_n) během poruchy.

3.2. Identifikace zkratových impulsů pomocí STMPM

Obrázek 9 ukazuje průběh všech rychlostí útlumu vzorového průběhu napětí v rozvodně po třífázovém zkratu s nulovou impedancí k zemi v uzlu 816 modelu. Je vidět, že nedostatek výběru rychlostí rozpadu ztěžuje lokalizaci pulzů; to platí zejména pro slabší pulsy. Na druhou stranu, vizuální pozorování rychlostí útlumu umožňuje snadnou identifikaci intervalů obsahujících pulsy v případě vizuální analýzy průběhů fázového napětí, i když to není vždy snadné v případě malých amplitud pulsů.

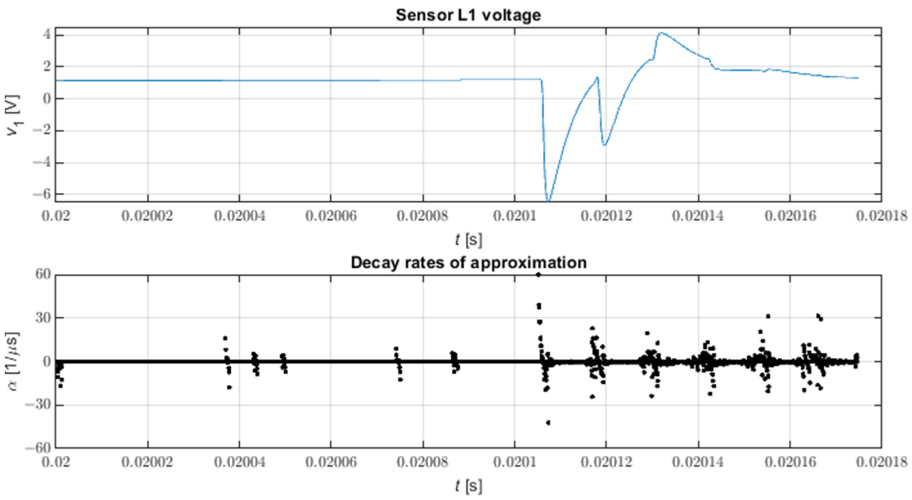
Obrázek 9. Všechny míry rozpadu aproximace STMPM. N = 9, L = 4.

Obrázek 10 ukazuje vybrané rychlosti útlumu spolu s lineární regresí použitou k identifikaci okamžiku příchodu pulzu. Počet detekcí falešných pulzů lze snížit odfiltrováním zbytečných koeficientů útlumu.

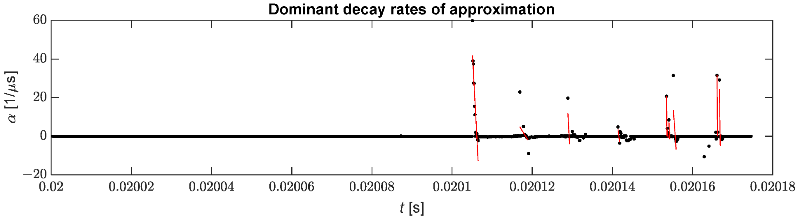
Obrázek 10. Vybrané rychlosti rozpadu použité pro identifikaci pulzu.

Tabulka 2 ukazuje chyby v identifikaci času příchodu první příchozí vlny na stanici. Tato chyba je definována následující rovnicí:

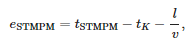
kde:

• t_STPMM – okamžik příjezdu podle STMPM,
• t_K – moment chyby,
• l —vzdálenost místa zkratu od rozvodny a
• v = 299 552 300 m/s – rychlost šíření poruchových vln měřená pro zkrat v nejvzdálenějším uzlu (838).

Parametry metody použité k získání výsledků jsou:

• N = 5 – počet vzorků za časové okno;
• L = 2 – parametr tužky;
• p = 6 – počet přesných platných desetinných míst měření;
• α_Thr=1051s – práh detekce pulsu;
• T_max=2,1 μs – maximální šířka pulzu;
• T_w=0,5 μs —šířka okna;
• T_s=0,1 μs – perioda vzorkování;
• r=0,02 V – práh amplitudy.

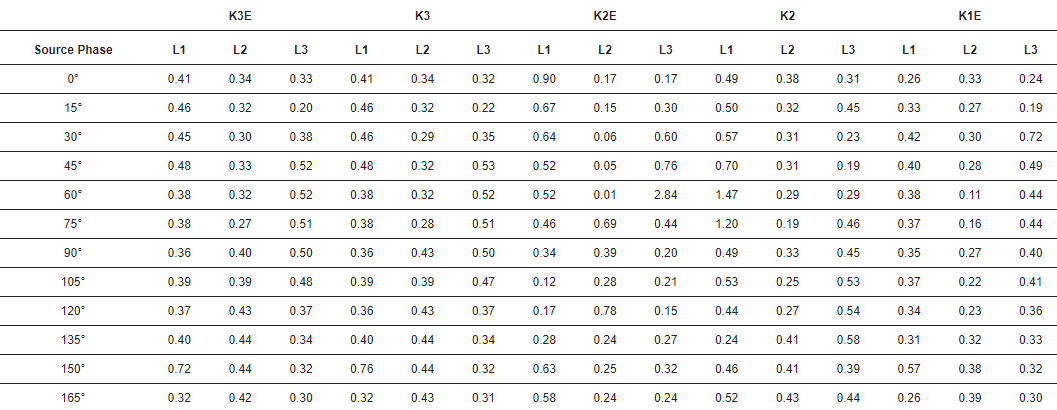
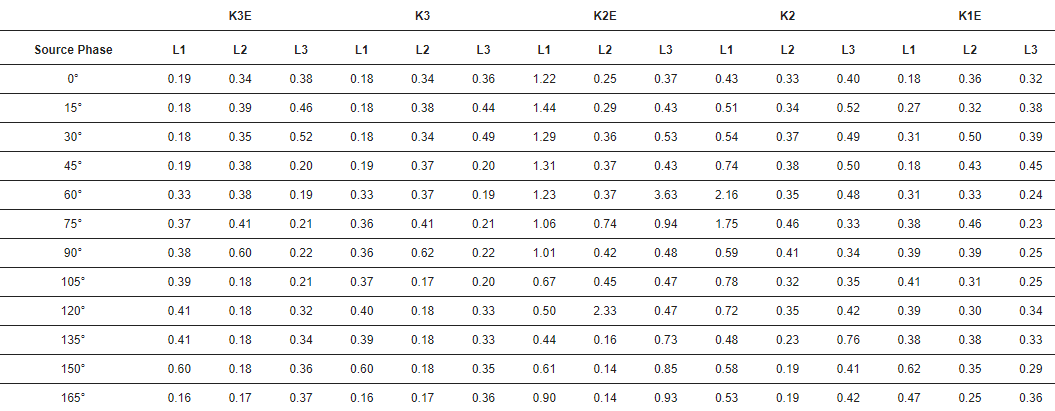
Tabulka 3 ukazuje standardní odchylky časové chyby pulsu.

Tabulka 2. Časová chyba identifikace vlny v případě různých poruch. Jednotka: µs. K3E – třífázová zemní porucha, K3 – třífázová porucha, K2E – dvoufázová zemní porucha, K2 – dvoufázová porucha, K1E – zemní porucha.

Tabulka 3. Směrodatná odchylka časové chyby. Jednotka: µs. K3E – třífázová zemní porucha, K3 – třífázová porucha, K2E – dvoufázová zemní porucha, K2 – dvoufázová porucha, K1E – zemní porucha.

4. Diskuse

Byl vyvinut model přenosové funkce odporového napěťového senzoru založený na širokopásmových měřeních od 10 Hz do 20 MHz. Simulace poruch generovaných postupných vln v modelu IEEE 34-bus byly provedeny pomocí přenosové funkce. Frekvenční odezva odporového snímače byla dostatečná pro identifikaci poruchových vln v sekundárním napěťovém signálu. Snímač transformuje signály postupné vlny s přibližně konstantním zesílením, které je větší než zesílení při síťové frekvenci. K identifikaci byl použit nový algoritmus reálného času založený na metodě maticové tužky. Varianta této metody použitá v článku se vyznačuje vysokou přesností identifikace vlny, protože průměrná chyba byla 0,41 µs při vzorkování 10 MHz a chyba měla kladnou hodnotu, takže nalezený čas příchodu byl větší než skutečný. Je však třeba poznamenat, že v praktických aplikacích metody, např. při vlnové lokalizaci poruch, je část této chyby eliminována díky diferenciálnímu provozu těchto algoritmů. Přesná identifikace poruchových vln může umožnit klasifikaci a lokalizaci poruch v sítích vysokého napětí pomocí přípojnic jako jediného měřicího bodu. Pro ověření účinnosti algoritmu a jeho porovnání s jinými metodami identifikace příchozích vlnových impulsů je vyžadován test využívající reálné signály. Zcela správná transformace napětí pomocí senzorů může umožnit klasifikaci typu poruchy na základě amplitud jimi generovaných vln.

Reference

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Článek od: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).