Die Identifizierung von Wanderwellen in einem Spannungssensorsignal in einem Mittelspannungsnetz mit der Kurzzeit-Matrix-Pencil-Methode

Bei den Tests wurde der von DACPOL SP bereitgestellte Omicron-Lab Bode 100 Vektorschaltungsanalysator verwendet. Z O.O.

Zusammenfassung

Die meisten Methoden zur Lokalisierung von Fehlerwellen basieren auf der Analyse des durch Stromwandler transformierten Leitungsstroms und sind auf Hochspannungsnetze beschränkt. Die Fehlerwellenortung in Mittelspannungsnetzen befindet sich noch in der Entwicklung. In diesem Beitrag wird ein neuer Echtzeit-Algorithmus zur Erkennung von Wanderwellen in einem Verteilnetz mittels Spannungssignal und Kurzzeit-Matrix-Pencil-Methode vorgestellt. Um die sekundärseitigen Spannungswellenformen am Umspannwerk zu erhalten, wurde das Modell eines resistiven Spannungssensors basierend auf den Breitbandmessungen von 10 Hz bis 20 MHz entwickelt. Der getestete Sensor verstärkt die mit Wanderwellen verbundenen Frequenzen mehr als die Netzfrequenz, was die Identifizierung ermöglicht. Kurzschlusssimulationen auf dem IEEE 34-Bus-Feeder wurden durchgeführt, um den Algorithmus zu testen. Das entwickelte Verfahren kann sogar Wellen mit geringer Amplitude erkennen.

1. Einführung

Der Schutz des Stromversorgungssystems vor Fehlern ist eines der Ziele der Schutzrelais. Die schnelle Beseitigung von Störungen begrenzt den Schaden, der an Stromversorgungsgeräten zugefügt wird, und reduziert seine negativen Auswirkungen auf die Qualität der elektrischen Energie. Daher ist die Entwicklung von schnellen und genauen Relais und Fehlerortern in Verteilnetzen sowohl aus technischer als auch aus wirtschaftlicher Sicht ein zentrales Thema. Bei Hochspannungsnetzen ist die Lokalisierung von Fehlern einfach, da sie durch eine große Streuung der Messungen und Schleifenstruktur gekennzeichnet sind. Bei Verteilnetzen werden Messungen hauptsächlich an einem einzelnen Punkt der dortigen Umspannstation durchgeführt. Darüber hinaus weisen Verteilungsnetze eine Baumstruktur auf, was die Identifizierung fehlerhafter Zweige unsicher macht. Die Lösung dieses Problems kann die Verwendung von Wanderwellenortungsgeräten sein, die in diesem Fall möglicherweise genauer sind als herkömmliche Verfahren. Um den Einsatz solcher Ortungsgeräte zu ermöglichen, ist es notwendig, möglichst genaue Methoden zur Wanderwellenidentifikation zu entwickeln.

Der herkömmliche Ansatz zur Fehlererkennung basiert auf der Analyse von Strömen und Spannungen einer Grundfrequenz. Aus diesem Grund erfordern Schutzalgorithmen, die auf solchen Signalen basieren, die Analyse eines Signalintervalls, das lang genug ist, um sicherzustellen, dass die Störung aufgetreten ist. Ein modernerer Ansatz basiert auf Wanderwellen, bei denen es sich um höherfrequente Signale handelt, die sich entlang von Stromleitungen ausbreiten. Diese Art des Schutzes wird manchmal als „Ultra-High-Speed“ bezeichnet. Es erkennt durch Fehler erzeugte Strom- und Spannungswellen. Dieser bestimmt dann sowohl die Art als auch den Ort der Störung anhand des Vergleichs ihrer Amplituden und Ankunftszeiten mit den Messgeräten. Der Hauptvorteil des wellenbasierten Schutzes ist zweifellos die Arbeitsgeschwindigkeit (weniger als 4 ms) [1]. Darüber hinaus funktioniert es korrekt mit serienkompensierten Übertragungsleitungen und während Power-Swings.

Die Fehlerortung mittels Wanderwellen kann in zweipolige und einpolige Schemata unterteilt werden. Bei Doppelpolrelais erfolgt die Messdatenerfassung an den Enden geschützter Leitungen und erfordert die Übertragung von Messdaten zwischen Geräten. Einpolige Relais werten jedoch die Signale von Strömen und Spannungen von nur einem Messpunkt aus. Hervorzuheben ist, dass sich Relais mit zwei Anschlüssen durch eine höhere Zuverlässigkeit auszeichnen, da sie direkt von der Störung erzeugte Wellen verwenden, um sie zu lokalisieren und zu klassifizieren. Diese Wellen haben die größtmögliche Amplitude und werden nach einem Fehler zuerst erkannt. Im Fall von Relais mit einem Anschluss basiert der Schutz jedoch auf der von der Störung erzeugten Welle und auf den Wellen, die von Leitungsunterbrechungen, Abzweigungen und dem Fehler selbst reflektiert werden [2]. Das liegt daran, dass im Netz kein zweiter Messpunkt vorhanden ist.

Hochspannungsnetze sind durch das Vorhandensein von Umspannwerken mit Messgeräten an den Leitungsenden gekennzeichnet. Daher werden hier Doppelpolrelais verwendet. Bei Verteilungsnetzen sind Hoch-/Mittelspannungs-Umspannwerke normalerweise der einzige Ort, an dem Schutzrelais mit Transformatoren oder Sensoren platziert werden. Dies bedeutet, dass in Verteilnetzen die Verwendung von Single-Ended-Wave-Relays die billigste Lösung ist.

Verteilernetze sind Netzwerke mit einer Baumtopologie, und diese Eigenschaft macht eine genaue Fehlerortung schwierig. Sowohl für konventionelle Fehlerortungsgeräte als auch für Wellenortungsgeräte ist die Situation komplizierter als in Übertragungsnetzen, da mehrere potenziell fehlerhafte Abzweigungen in bekannter Entfernung von der Umspannstation vorhanden sein können. Nur einer der Zweige ist fehlerhaft. Eine kurzgeschlossene Leitung kann jedoch festgestellt werden, indem die Amplituden der Stromwellen verglichen werden, die an den Bussen der Umspannwerke gestreut werden [2,3,4].

Verschiedene Methoden zur Lokalisierung von Fehlern wurden vorgeschlagen, wie z. B. die Erkennung von Frequenzen, die mit Wellenoszillationen zwischen Knoten verbunden sind [5], Vergleich des gemessenen Stroms mit dem vorhergesagten für einen gegebenen Kurzschlussort [6] und traditionellere Methoden basierend auf der Erkennung von Verwerfungswellenfronten [3,7]. Die folgenden Methoden wurden verwendet, um Wellenfronten zu detektieren: Wavelet-Transformation, Hauptkomponentenanalyse basierend auf Merkmalsextraktion, Teager-Energieoperator, Ensemble-empirische Modenzerlegung und die Matrix-Pencil-Methode, die in diesem Artikel diskutiert und verwendet wird [8,9]. Die Matrix-Pencil-Methode wird verwendet, um ein Signal in die Summe exponentiell gedämpfter Sinuskurven zu zerlegen [10]. Auf dem Gebiet der elektrischen Energietechnik wurde die Matrix-Pencil-Methode verwendet, um die Grundmoden von Schwingungen aufgrund von Fehlern abzuschätzen und Harmonische und Subharmonische abzuschätzen [11,12, 13].

Elektrische Signale, die von digitalen Datenverarbeitungsalgorithmen verarbeitet werden, werden mit Hilfe von Messgeräten, die sich auf der Station befinden, an das Relais geliefert. Zu diesen Geräten gehören Strom- und Spannungswandler, Rogowski-Spulen oder Sensoren, die den Pegel elektrischer Signale auf den für die Relais akzeptablen Pegel reduzieren. Wichtig ist, dass das Signal auf der Sekundärseite dieser Geräte möglichst genau wiedergegeben und idealerweise nur skaliert wird. In der Praxis haben die Messgeräte jedoch je nach Signalfrequenz variable Verstärkung und Phasenverschiebung. Hohe Frequenzen sollten vom Instrument nicht zu stark gedämpft werden, um eine ankommende Wanderwelle erkennen zu können, die eine sich schnell ändernde Wellenform ist und daher hochfrequente Komponenten enthält. Es muss betont werden, dass das Instrument eine konstante Zeitverzögerung (vorzugsweise überhaupt keine) einführen sollte, um die Amplitude der Fehlerwelle genau zu reproduzieren, und dass seine Verstärkungseigenschaften so wenig variabel wie möglich sein sollten.

Transformatoren sind die Instrumente, die traditionell in der Elektrizitätsindustrie zur Spannungsmessung verwendet werden. Sie zeichnen sich durch eine sehr präzise Transformation elektrischer Signale aus, haben aber auch Nachteile. Sie tragen zum negativen Phänomen der Ferroresonanz bei, sind Schäden durch Kurzschlüsse im Sekundärkreis ausgesetzt und können hochfrequente (>3 kHz) Spannungsanteile nicht präzise transformieren [14]. Aus diesem Grund wurden unkonventionelle Sensoren entwickelt, die auf Mechanismen basieren, die sich vom Transformatorsystem unterscheiden, als Antwort auf die Notwendigkeit, transiente Komponenten genau zu messen [15 ,16].

Für Spannungsmessungen sind Spannungssensoren, die auf kapazitiven (C), resistiven (R) und resistiv-kapazitiven (RC) Teilern basieren, beliebte unkonventionelle Sensoren [14]. Insbesondere R- und RC-Teiler sind die beliebtesten, da sie aufgrund vernachlässigbarer Induktivität keine Ferroresonanz induzieren können, Transienten und hohe Frequenzen genau umwandeln, die Entladung angesammelter Ladung auf der Leitung ermöglichen und sekundärseitig kurzschlüssefest sind. Diese Teiler können erfolgreich für Netzqualitätsmessungen und zur Kurzschlussortung anhand von Wellenphänomenen eingesetzt werden.

Die Literatur zur Modellierung herkömmlicher Transformatoren ist umfangreich, bezieht sich aber leider normalerweise auf die Beschreibung ihrer Eigenschaften bei Frequenzen unter 10 kHz [15,17]. Darüber hinaus konnten die Autoren die numerischen Daten der Bode-Plots oder Übertragungsfunktionen von Spannungswandlern (sowoh konventionellen als auch unkonventionellen) bis zu 1 MHz nicht finden, selbst in den Artikeln, die die Studien auf diesem Gebiet beschreiben [18,19]. Solche Daten sind für einen herkömmlichen Stromwandler verfügbar l[20]. Natürlich unterscheiden sich Sensoren im Design, was zu Variationen ihrer Übertragungseigenschaften von einem Typ zum anderen führt, aber die Kenntnis der Übertragungsfunktion eines Beispiels scheint erforderlich zu sein.

Um solche Daten zu erhalten, wurden Messungen der Frequenzeigenschaften eines Mittelspannungssensors durchgeführt. Dann wurden sie verwendet, um sein Übertragungsfunktionsmodell zu entwickeln. Anschließend wurde das verbesserte Kurzzeit-Matrix-Pencil-Verfahren in Anwendung zur Detektion von Spannungskurzschlusswellen im Mittelspannungsnetz, gemessen auf der Sekundärseite von Spannungssensoren, vorgestellt.

Die Struktur des Papiers ist wie folgt. Abschnitt 2 beschreibt die Kurzzeit-Matrix-Pencil-Methode mit ihrer Anwendung zum Auffinden von Signalimpulsen. Es wird auch der Algorithmus zur Identifizierung der Pulse bereitgestellt. Abschnitt 3 enthält Messergebnisse der Spannungssensor-Übertragungsfunktion und Ergebnisse der Operation des Algorithmus auf der Grundlage von durchgeführten Simulationen. Schlussfolgerungen finden sich in Abschnitt 4.

2. Die Identifizierung von Fehlerimpulsen in einem Mittelspannungsnetz

2.1. Die Kurzzeit-Matrixstift-Methode

Die Short-Time-Matrix-Pencil-Methode (STMPM) approximiert ein Signal innerhalb des Fensters, das sich mit der Zeit als Summe sinusförmiger Komponenten mit einer exponentiell variablen Amplitude bewegt [10,21]:

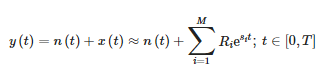
wo:

• y(t) – Messsignal,
• n(t) – Rauschen,
• x(t) – ursprüngliches Signal,
• Ri – Residuen oder komplexe Amplituden von Komponenten,
• Si – komplexe Pole und
• M – Anzahl der Approximationskomponenten.

Für ein abgetastetes Signal t = kT_s nimmt die obige Gleichung die folgende Form an:

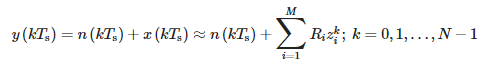
wo:

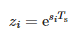
• Ts – Stichprobenzeitraum und
• N – Anzahl der Proben.

Um die Näherungsparameter zu bestimmen, soll die folgende Matrix konstruiert werden:

Hier ist L ein Pencil-Parameter. Die Anzahl der Approximationskomponenten M erfüllt die folgende Beziehung:

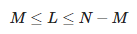
So sehen wir, dass der Maximalwert von M gleich ⌊N/2⌋ ist.
Indem wir die Matrix Y einer Singulärwertzerlegung (SVD) unterziehen, erhalten wir:

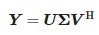
wo:

• U – einheitliche Matrix der Größe (N − L) × (N − L),
• Σ – rechteckige Diagonalmatrix von Einzelwerten mit der Größe (N − L) × (L + 1) und
• V – einheitliche Matrix der Größe (L + 1) × (L + 1).

Wenn das gemessene Signal kein Rauschen enthalten würde, würde die Σ-Matrix genau M Singular ungleich Null enthalten Werte. Durch das Rauschen können die Singularwerte verfälscht werden, was sich durch zusätzliche kleine Singularwerte äußert. Der Rauscheffekt wird eliminiert, indem diese kleinen Werte entfernt werden. Es bleiben nur M dominante Werte übrig, die die folgende Bedingung erfüllen:

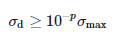
wobei σ_max ein dominanter Singularwert ist und p die Anzahl der genauen signifikanten Dezimalstellen der Messung ist.

Dann werden Untermatrizen der resultierenden SVD-Matrizen konstruiert:

1. Matrix U′=[u1,u2,…,u_M] der Größe (N − L) × M wird erzeugt, indem Spalten belassen werden, die den singulären Werten entsprechen, die Bedingung (7) erfüllen, und entfernt werden die anderen;
2. Die quadratische Diagonalmatrix Σ=diag(σ1,σ2,…,σM) wird gebildet, indem die Spalten und Zeilen der Σ-Matrix entfernt werden, die einzelne Werte enthalten, die Bedingung (7) nicht erfüllen;
3. Matrix V′=[v1,v2,…,v_M] der Größe (L + 1) × M wird gebildet, indem die Spalten, die den singulären Werten entsprechen, die Bedingung (7) erfüllen, und belassen werden die anderen entfernen.

Dann wird die Matrix V₁′ erstellt, indem die letzte Zeile der V′-Matrix entfernt wird. V₂′ wird erstellt, indem die erste Zeile der V′-Matrix entfernt wird.

Dann werden die folgenden Matrizen berechnet:

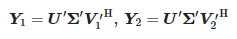
Werte zi sind verallgemeinerte Eigenwerte ungleich Null von Matrizenpaaren (Y₁, Y₂), nämlich Eigenwerte von Y ^†₁Y₂, wobei Y^†₁ ist die Moore-Penrose-Pseudoinverse von Y₁. Dann berechnen wir Pole:

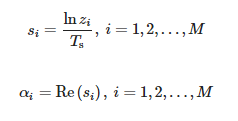
Die Werte der Amplituden können wie folgt ermittelt werden:

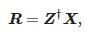
wo:

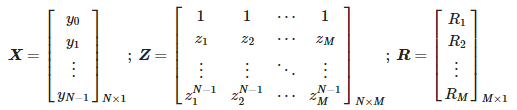
Die obigen Operationen werden in der Kurzzeit-Matrixstiftmethode für aufeinanderfolgende Datenintervalle durchgeführt [9,22].

Die ungefähren Ergebnisse von Eigenwerten, Pseudoinversionen und SVD-Algorithmen können das Auftreten von zi-Werten ungleich Null, obwohl sie nahe Null liegen, beeinflussen. Diese Werte wirken sich auf die MPM-Geschwindigkeit aus und können deren Ergebnisse negativ beeinflussen, daher lohnt es sich, sie vor der Berechnung der Residuen zu entfernen.

2.2. Das Verhalten der Komponentenpole in der Nähe eines Pulses

Fehler im Stromnetz erzeugen Impulse, die sich entlang der Stromleitungen mit annähernd Lichtgeschwindigkeit ausbreiten [3]. Diese Impulse können unter Verwendung der Polverschiebungsanalyse der STMPM-Näherung identifiziert werden. Abbildung 1 zeigt drei beispielhafte gaußförmige Pulse und die Pole ihrer Approximation mit STMPM. Wenn der Impuls kommt, ändert sich die Annäherung mit exponentiellen Komponenten, wenn sich das Zeitfenster bewegt. Wenn der Impuls rechts vom Mittelpunkt des Fensters liegt, haben die Pole der Näherung einen positiven Realteil, wenn der Gaußsche Scheitelpunkt in der Mitte des Fensters liegt, ist der Realteil der Pole nahe Null, und wenn der Puls ist in der ersten Hälfte des Fensters, die Pole haben einen negativen Realteil. Die Änderung des Vorzeichens des Realteils der Pole zeigt daher an, dass die Mitte des Pulses durch den Mittelpunkt des Abtastfensters [0, 22]. Wir können auch aus Abbildung 2 ersehen, dass die Pole mit dem größten Absolutwert des Realteils (und daher mit der schnellsten Amplitudenänderungsrate) den größten Wert des anfänglichen Amplitudenmoduls (Residuum) haben.

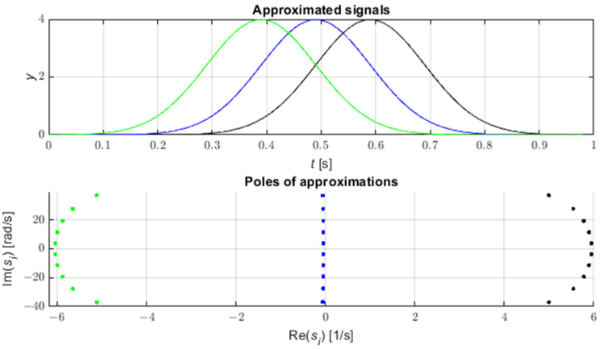
Abbildung 1. Gaußsche Werte und entsprechende Näherungspole.

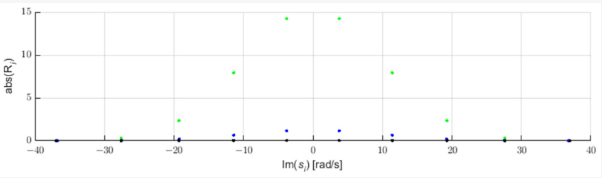
Abbildung 2. Reste von Komponenten der Gaußschen Näherung.

Wir sehen also, dass die zeitliche Koordinate der Pulsspitze näherungsweise mit dem Moment des Vorzeichenwechsels der Dämpfungskoeffizienten identifiziert werden kann.

Indem wir den zeitabhängigen Verlauf dieser Koeffizienten unter Verwendung von STMPM erhalten, können wir sie in der Nähe des Punktes, an dem die Koeffizienten durch Null gehen, einer linearen Approximation unterziehen und eine ungefähre Pulsspitzenkoordinate erhalten. Es sei darauf hingewiesen, dass die Koeffizienten mit der höchsten Variabilität auch die höchste Amplitude aufweisen – sie sind die größten Komponenten des Pulses.

2.3. Der Echtzeit-Pulserkennungsalgorithmus

Das Flussdiagramm des Algorithmus zur Erkennung von Impulsen, die von Wanderwellen stammen, ist in Abbildung 3 dargestellt. Der Algorithmus unterzieht aufeinanderfolgende Fenster des Signals STMPM, um Abklingraten der Näherungskomponenten zu extrahieren.

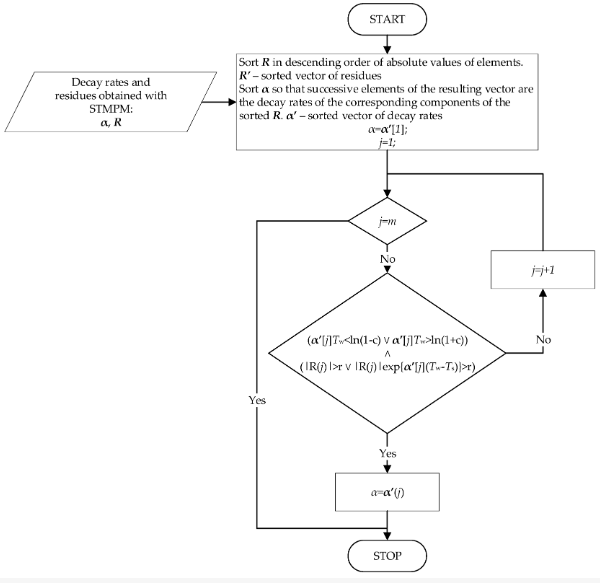
Abbildung 3. Der Algorithmus zur Auswahl der Zerfallsraten.

Die erhaltenen Komponenten werden einer Auswahl unterzogen, deren Verfahren in Abbildung 4 dargestellt ist. Die Auswahl basiert auf der Annahme, dass diejenigen Komponenten des STMPM, die durch die größte Amplitude gekennzeichnet sind, für die Spitzenzeit genommen werden sollten Annäherung – sie bilden den größten Beitrag zur transienten Komponente des Signals. Dies stimmt mit der Beobachtung aus dem vorherigen Punkt überein – die Komponenten mit der größten Amplitudenvariation sind durch die größte Anfangsamplitude gekennzeichnet. Für den Fall, dass die Komponente mit der größten Amplitude während des gesamten Fensters der Länge T_w durch eine kleine Abklingrate gekennzeichnet ist – kleiner als der Parameter c – oder ihr maximaler Beitrag zum Signal kleiner als r ist, die nächste Komponente hinsichtlich der Amplitudengröße wird als potentieller Kandidat für die Abklingrate α ausgewählt. Durch Wiederholen dieses Verfahrens für nachfolgende Komponenten, bis die Bedingung erfüllt ist, erhält man schließlich den Koeffizienten α, der dann verwendet wird, um die Impulsankunftszeit anzunähern. Wenn keine der Komponenten die obigen Bedingungen erfüllt, wird die mit der höchsten Amplitude ausgewählt.

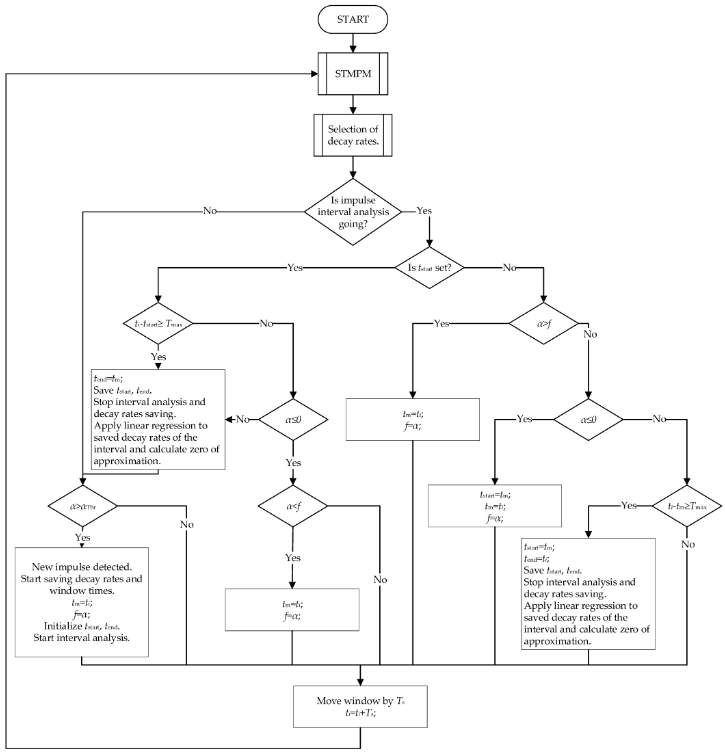
Abbildung 4. Der Algorithmus der Pulserkennung.

Die einem Fenster zugeordnete Zeit gilt als:

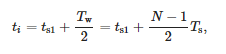
wobei t_s1 – Zeit der ersten Fensterprobe und T_w – Fensterbreite.

Das Eintreffen eines Impulses wird durch einen starken Anstieg der α-Raten angezeigt, der mit einer schnellen Änderung des Signals am Ende des Abtastfensters verbunden ist. Als Schwellwert der Abklingraten wird der Parameter α_Thr gewählt. Wenn die Erfassungsschwelle überschritten wird, werden die nachfolgenden Werte von α-Koeffizienten und Fensterzeiten in den Speicher geschrieben, und die Datenanalyse wird gestartet, um genauere Impulsgrenzen zu bestimmen. Der Zeitpunkt t_Start mit dem höchsten Wert von α vor dem Wechsel des Vorzeichens der Abklingrate wird als richtiger Beginn des Pulses gewählt. Um die möglichen Zeitpunkte der korrekten Pulsgrenzen zu speichern, wurde die Variable t_m eingeführt, wobei die Variable f die größten Werte von α des bisher berechneten Pulses enthält.

Wenn der Wert von t_start gefunden wird, beginnt die Suche nach dem endgültigen richtigen Ende des Impulses t_end. Dies entspricht dem kleinsten Wert von α, bevor sich das Vorzeichen wieder ändert, diesmal ins Positive. Die Variable i_m wird erneut verwendet, um die vorherigen potentiellen Endpunkte zu speichern. Die Variable f enthält die vorherigen minimalen α-Werte.

Wenn die Impulslänge gleich dem T_max der Proben ist oder das Ende des Impulses gefunden wird, wird die Analyse des Impulses beendet.

Funktion α(t) im Intervall [t_start; t_end] wird einer linearen Regression unterzogen. Die Koeffizienten dieser Regression werden als Lösung für folgendes Problem gefunden:

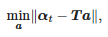
wobei: α_t=[α(t_start),α(t_start+Ts),…,α(t_end)]^T, a=[a₁,a₀]^T

Die gesuchten Koeffizienten sind:

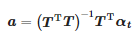
Während der Moment der Ankunft des Impulses ist:

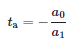
2.4. Der angepasste IEEE 34-Bus Test Feeder

Für Kurzschlussberechnungen wurde ein 34-Bus-IEEE-Test-Feeder-Modell in Simulink erstellt. Die Topologie des Feeders ist in Abbildung 5 dargestellt [23]. Der Feeder basiert auf einem realen Netzwerk im Bundesstaat Arizona. Es ist einfach genug, um bei transienten Simulationen mit kleinen Integrationsschritten keine wesentliche Rechenlast zu werden. Das Modell wurde vereinfacht und die Parameter geändert, um die europäischen Gitter nachzuahmen:

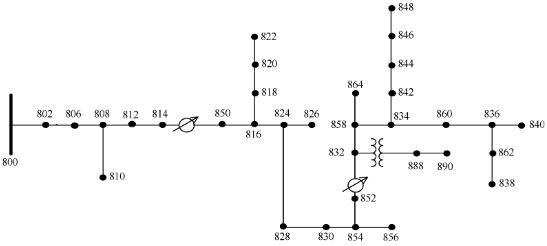
Abbildung 5. Die IEEE 34-Bus-Feeder-Topologie.

• Die Netzspannung wurde von 24,9 kV auf 16,5 kV geändert;
• Alle Abschnitte der Stromleitungen wurden als Freileitungen mit den gleichen Parametern angenommen;
• Spannungsregler wurden entfernt;
• Es wurde angenommen, dass die verteilten Lasten bei Bussen am anderen Ende der belasteten Linien in einen Topf geworfen werden;
• Verbraucher wurden über Verteiltransformatoren an das Mittelspannungsnetz angeschlossen;
• Neutralpunkt des Hoch-/Mittelspannungstransformators wurde von der Erdung getrennt.

Parameter der Spannungsquelle:

• 50-Hz-Frequenz;
• 115,5 kV Netzspannung;
• Widerstand 0,00227 Ω.
• Symmetrische Quelle mit Phasenverschiebung der L1-Phase gleich 0°.

Parameter des Leistungstransformators:

• Spannungsverhältnis 115,5/16,5;
• Schaltgruppe der Hochspannungswicklung Yg;
• Schaltgruppe der Niederspannungswicklung D11;
• Leistung 6,3 MVA;
• Relative Kurzschlussspannung 7,5 %;
• Kurzschlusswiderstand gleich 0,49 % der äquivalenten Impedanz.

Parameter der Verteilungstransformatoren:

• Spannungsverhältnis 15,75/0,4;
• Schaltgruppe der Hochspannungswicklung D11;
• Schaltgruppe der Niederspannungswicklung Yg;
• Leistung 630 kVA;
• Relative Kurzschlussspannung 6 %;
• Kurzschlusswiderstand gleich 17,2 % der äquivalenten Impedanz.

Parameter der Stromleitungen:

• Dreiphasenleitung ohne Neutralleiter;
• Ein Leiter pro Phase;
• Leiterdurchmesser 0,8466 cm;
• T/D-Verhältnis 0,311;
• Gleichstromwiderstand 0,5939 Ω/km;
• Horizontale Positionen der Leiter x=[−1.05, 0, 1.05];
• Vertikale Positionen der Leiter u=[−9.05, 10.61, 9.05];
• Erdungswiderstand ρ=100 Ωm.

An jeden Transformator wurden Kapazitäten angeschlossen, wie in Abbildung 6 [5] in um die Eigenschaften der Transformatoren bei hohen Frequenzen zu modellieren.

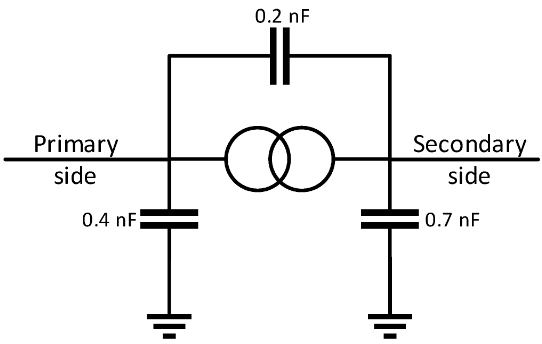
Abbildung 6. Transformer-Modell.

Stromleitungen wurden zwischen 1 Hz und 1 MHz modelliert, wobei der Skin-Effekt unter Verwendung des universellen Leitungsmodells berücksichtigt wurde.

Simulationen von einphasigen und mehrphasigen Kurzschlüssen mit Nulldurchgangswiderstand wurden bei 20 %, 50 %, 80 % und 100 % Leitungslänge durchgeführt. Er entspricht 76 Kurzschlussstellen. Der Integrationsschritt der Simulation war Δt=0,1 μs. Tustin/Backward Euler war die verwendete Integrationsmethode.

3. Ergebnisse

3.1. Messungen der Transmissionseigenschaften des Mittelspannungssensors

Die Messungen des Frequenzgangs wurden für einen Mittelspannungssensor durchgeführt, der für den Einbau in Steckerköpfe vorgesehen ist. Der Sensor war ein Widerstandsteiler mit einer Nennprimärspannung von 20/√3 kV und einer Nennsekundärspannung von 3,25/√3, was dem Spannungsverhältnis von entspricht:

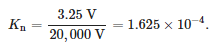
Für die Messungen wurde der Vektornetzwerkanalysator Bode 100 von OMICRON Lab verwendet. Dieses Gerät ermöglicht Messungen im Bereich von 1 Hz bis 50 MHz. Zur Durchführung der Tests wurde die Verstärkungs- und Phasenmessfunktion des Geräts verwendet. Diese Funktion basierte auf dem Vergleich von Amplitude und Phase der Spannungssignale auf der Primär- und Sekundärseite des Sensors. Die Messung der Übertragungsfunktion, definiert als Verhältnis der Spannung auf der Sekundärseite zur Spannung auf der Primärseite, wurde für 2048 Frequenzwerte im Bereich von 10 Hz bis 20 MHz durchgeführt. Die gemessenen Werte sind in Abbildung 7 dargestellt.

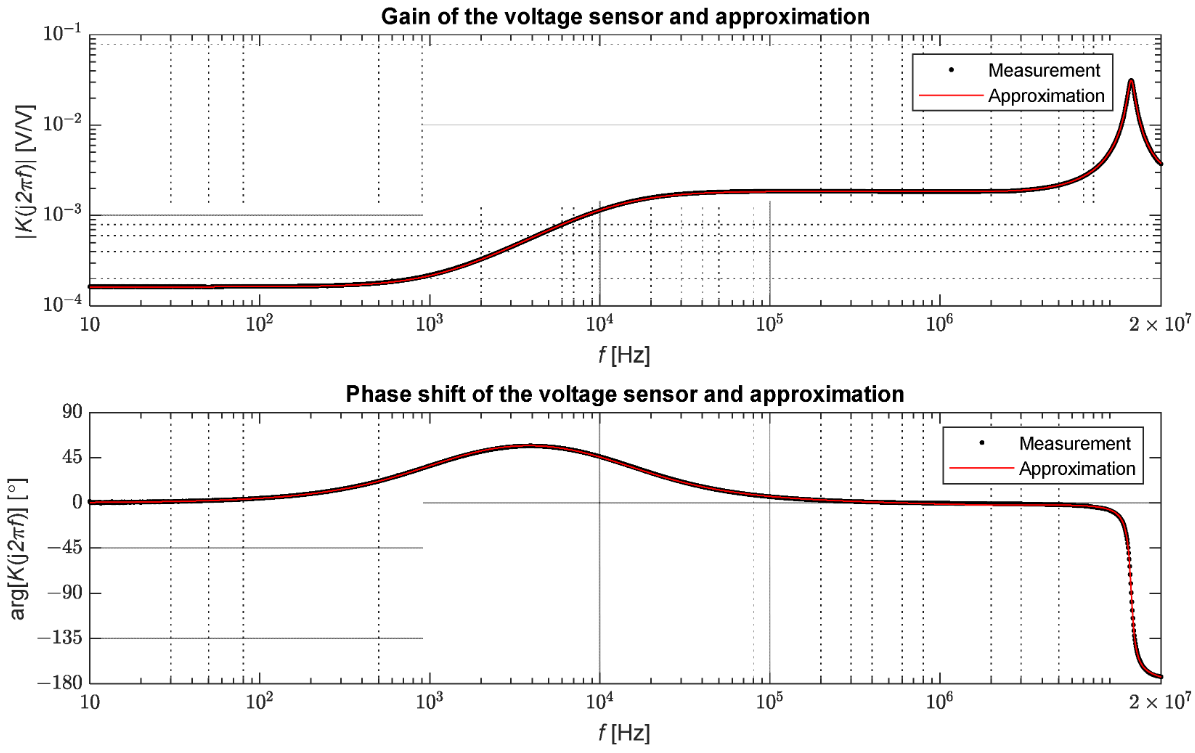
Abbildung 7. Messergebnisse des Transmissionsgrades des Mittelspannungssensors.

Der getestete Spannungssensor behält einen nominellen Übertragungskoeffizienten für Signale bis zu einer Frequenz von etwa 1 kHz bei, dann steigt die Kurve auf den Verstärkungspegel von etwa 1,84 × 10⁻³ an; dieser Pegel wird zwischen etwa 12,5 kHz und 6,6 MHz gehalten. Bedingt durch die differenzierende Eigenschaft des Sensors ergibt sich hier im Übergangsbereich von 100 Hz auf 100 kHz eine positive Phasenverschiebung von ca. 57°. Bei der Phase können wir zwei Zonen unterscheiden, bei denen der Versatz 6° nicht überschreitet. Der Frequenzbereich reicht dabei bis etwa 130 Hz und von 105 kHz bis 9,4 MHz. Daraus kann geschlossen werden, dass im Bereich von 105 kHz bis 6,6 MHz die Signale proportional transformiert werden, jedoch mit einem anderen Proportionalitätsfaktor als nahe der Netzfrequenz. Bei Wellenphänomenen reicht dieser Bereich aus, um die Form der sich in einem Gitter ausbreitenden Wellen genau darzustellen [20]. Dabei ist zu beachten, dass Spannungssensoren unterschiedlicher Bauart unterschiedliche Übertragungseigenschaften aufweisen können.

Um ein mathematisches Modell des Sensors zu entwickeln, wurde die „tfest“-Funktion von MATLAB verwendet, um die erhaltenen Daten durch eine stabile Übertragungsfunktion der folgenden Form anzunähern:

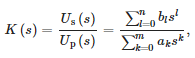
wo:

• Up(s) – Spannung auf der Primärseite des Sensors,
• Us(s) – Spannung auf der Sekundärseite des Sensors,
• n – die Reihenfolge des Zählers,
• m – die Reihenfolge des Nenners und
• ak, bl —Koeffizienten von Polynomen des Nenners und Zählers der Durchlässigkeit, nacheinander.

Die Werte der Übertragungsfunktionskoeffizienten sind in Tabelle 1 dargestellt. Es ist erwähnenswert, dass die modellierte Durchlässigkeit richtig ist, da die Ordnung des Nenners größer ist als die Ordnung des Zählers. Abbildung 7 zeigt auch den Vergleich der aus Messungen erhaltenen Übertragungsfunktionen mit der Näherung durch Formel (19). Der mittlere quadratische Fehler zwischen den Messpunkten und der durch die folgende Beziehung bestimmten Näherung wurde ebenfalls berechnet:

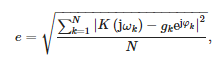
wo:

• N = 2048 – Anzahl der Messhäufigkeiten
• g_k – gemessene Verstärkung des Sensors bei Pulsation ω_k und
• φ_k – gemessene Phasenverschiebung des Sensors bei Pulsation ω_k.

Der Näherungsfehlerwert ist gleich:

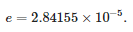
Tabelle 1. Werte der Polynomkoeffizienten des äquivalenten Transmissionsgrades eines Spannungssensors mit Widerstandsteilerstruktur.

Abbildung 8 zeigt den Vergleich der aus der Simulation erhaltenen Wellenform der Phasenspannung am Umspannwerk und der Spannung am Ausgang des modellierten Sensors im Fall eines direkten dreiphasigen Kurzschlusses mit der Erde am Knoten 816. Das ist es deutlich sichtbar, dass die Verstärkung von schnellen Transienten größer ist als von langsamen Transienten. Es ist erwähnenswert, dass diese Wellenformen fast proportional verstärkt werden.

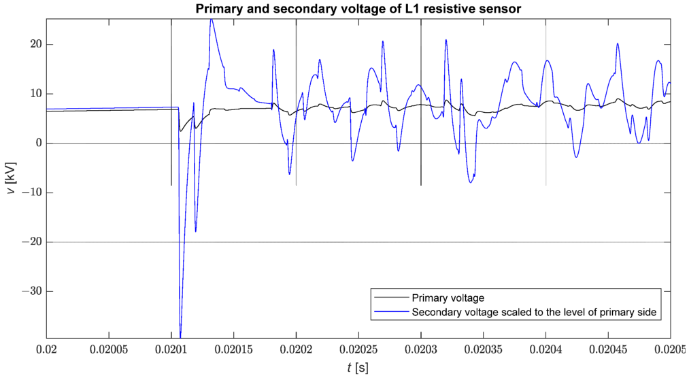
Abbildung 8. Vergleich der Wellenform der Phasenspannung (v_L1) und der Spannung am Ausgang des Sensors skaliert auf die Primärspannung (v_L1/K_n) während des Fehlers.

3.2. Die Identifizierung von Kurzschlussimpulsen mit STMPM

Fig. 9 zeigt die Wellenform aller Abfallraten einer beispielhaften Spannungswellenform an einem Umspannwerk nach einem dreiphasigen Nullimpedanz-Kurzschluss zur Erde am Knoten 816 des Modells. Es ist ersichtlich, dass das Fehlen einer Auswahl von Zerfallsraten es schwierig macht, Pulse zu lokalisieren; dies gilt insbesondere für schwächere Pulse. Andererseits ermöglicht die visuelle Beobachtung der Abklingraten bei der visuellen Analyse von Phasenspannungsverläufen eine einfache Identifizierung von Intervallen, die Pulse enthalten, obwohl dies bei kleinen Pulsamplituden nicht immer einfach ist.

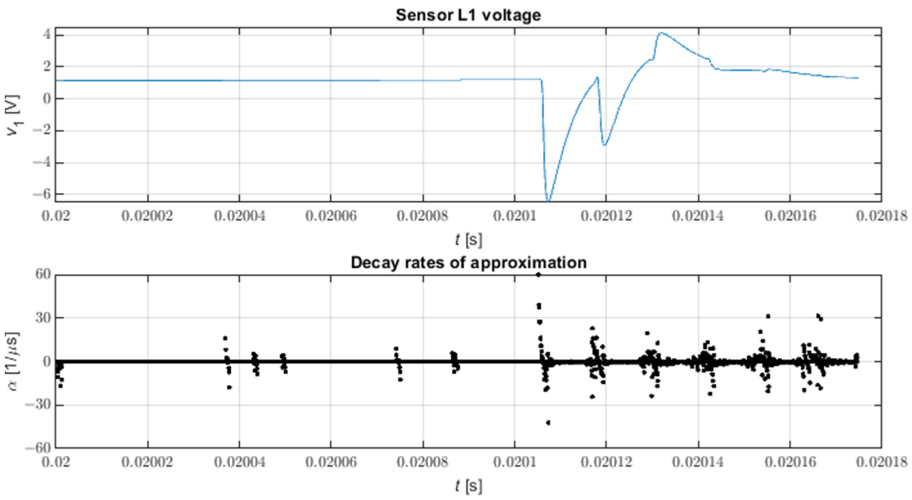
Abbildung 9. Alle Zerfallsraten der STMPM-Näherung. N = 9, L = 4.

Abbildung 10 zeigt die ausgewählten Abklingraten zusammen mit der linearen Regression, die verwendet wurde, um den Moment der Impulsankunft zu identifizieren. Die Anzahl der Fehlimpulserkennungen kann reduziert werden, indem unnötige Dämpfungskoeffizienten herausgefiltert werden.

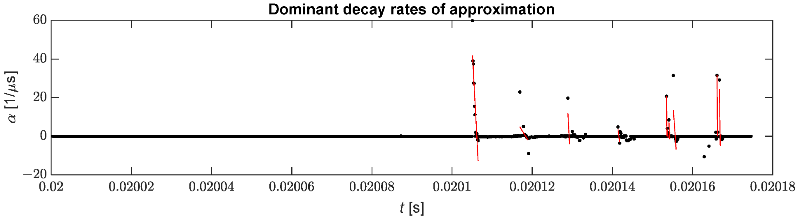
Abbildung 10. Ausgewählte Abklingraten, die zur Pulsidentifizierung verwendet werden.

Tabelle 2 zeigt die Fehler bei der Identifizierung der Ankunftszeit der ersten ankommenden Welle an der Station. Dieser Fehler wird durch die folgende Gleichung definiert:

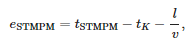
wo:

• t_STMPM – Ankunftszeitpunkt gemäß STMPM,
• t_K – Fehlermoment,
• l —Entfernung der Kurzschlussstelle von der Umspannstation und
• v = 299.552.300 m/s – Ausbreitungsgeschwindigkeit von Fehlerwellen, gemessen für einen Kurzschluss am entferntesten Knoten (838).

Die zum Erhalten der Ergebnisse verwendeten Methodenparameter sind:

• N = 5 – Anzahl der Abtastungen pro Zeitfenster;
• L = 2 – Bleistiftparameter;
• p = 6 – die Anzahl der genauen signifikanten Dezimalstellen der Messung;
• α_Thr=1051s – Pulserkennungsschwelle;
• T_max=2,1 μs – maximale Impulsbreite;
• T_w=0,5 μs – Fensterbreite;
• T_s=0,1 μs – Abtastperiode;
• r=0,02 V – Amplitudenschwelle.

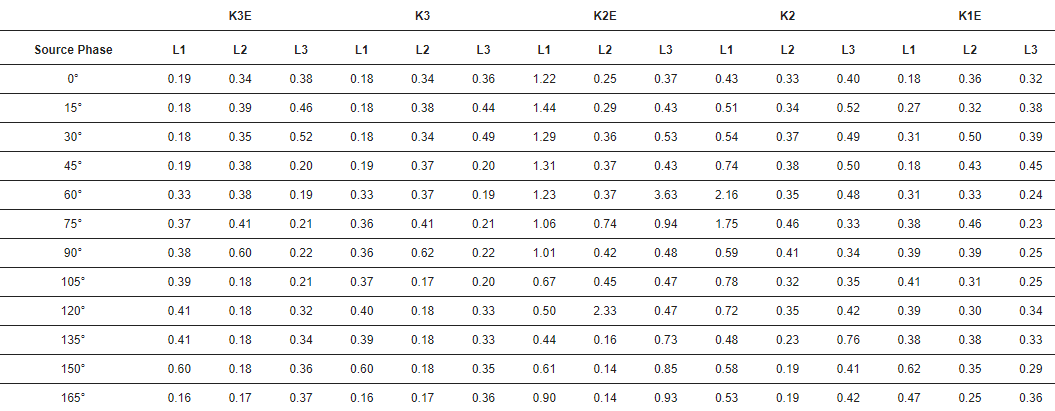
Tabelle 3 zeigt die Standardabweichungen des zeitlichen Fehlers des Pulses.

Tabelle 2. Zeitlicher Fehler der Wellenidentifikation bei verschiedenen Fehlern. Einheit: µs. K3E – Dreiphasen-Erdschluss, K3 – Dreiphasen-Fehler, K2E – Zweiphasen-Erdschluss, K2 – Zweiphasen-Fehler, K1E – Phase-Erde-Fehler.

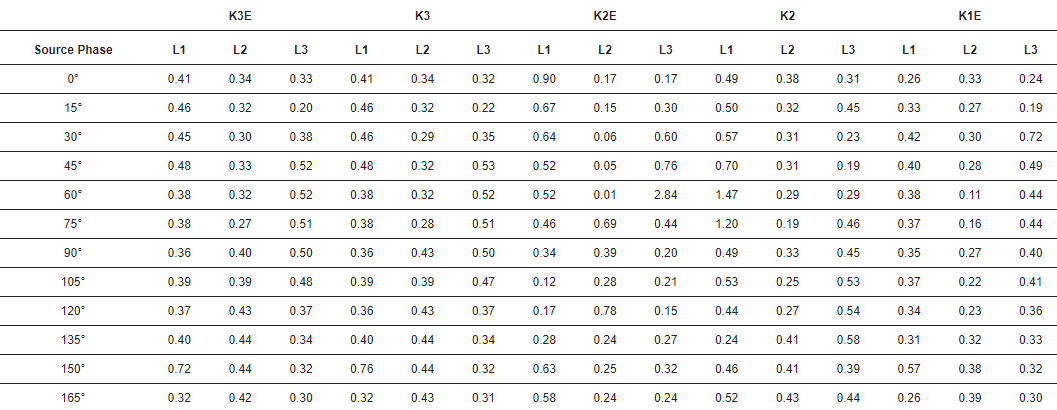
Tabelle 3. Standardabweichung des zeitlichen Fehlers. Einheit: µs. K3E – Dreiphasen-Erdschluss, K3 – Dreiphasen-Fehler, K2E – Zweiphasen-Erdschluss, K2 – Zweiphasen-Fehler, K1E – Phase-Erde-Fehler.

4. Diskussion

Das Übertragungsfunktionsmodell eines resistiven Spannungssensors basierend auf den Breitbandmessungen von 10 Hz bis 20 MHz wurde entwickelt. Die Simulationen von fehlererzeugten Wanderwellen im IEEE 34-Busmodell wurden unter Verwendung der Übertragungsfunktion durchgeführt. Der Frequenzgang des Widerstandssensors war ausreichend, um Störwellen im Sekundärspannungssignal zu erkennen. Der Sensor wandelt Wanderwellensignale mit ungefähr konstanter Verstärkung um, die größer ist als die Verstärkung bei der Netzfrequenz. Zur Identifizierung wurde ein neuer Echtzeitalgorithmus auf Basis der Matrix-Pencil-Methode verwendet. Die in der Arbeit verwendete Variante dieser Methode zeichnet sich durch die hohe Genauigkeit der Wellenidentifikation aus, da der durchschnittliche Fehler 0,41 µs bei 10 MHz Abtastung betrug und der Fehler einen positiven Wert hatte, sodass die gefundene Ankunftszeit größer war als die tatsächliche. Es sollte jedoch beachtet werden, dass in praktischen Anwendungen des Verfahrens, zB bei der Wellenlokalisierung von Fehlern, der Teil dieses Fehlers aufgrund des differentiellen Betriebs dieser Algorithmen eliminiert wird. Die genaue Identifizierung von Fehlerwellen kann es ermöglichen, Fehler in Mittelspannungsnetzen mit Sammelschienen als einzigem Messpunkt zu klassifizieren und zu lokalisieren. Ein Test mit realen Signalen ist erforderlich, um die Wirksamkeit des Algorithmus zu überprüfen und ihn mit anderen Methoden zur Identifizierung eingehender Wellenimpulse zu vergleichen. Eine recht korrekte Spannungstransformation durch Sensoren kann die Klassifizierung der Fehlerart anhand der Amplituden der von ihnen erzeugten Wellen ermöglichen.

Verweise

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Artikel von: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).