La identificación de ondas viajeras en una señal de sensor de voltaje en una red de voltaje medio utilizando el método de lápiz de matriz de tiempo corto

En las pruebas se utilizó el analizador vectorial de circuitos Omicron-Lab Bode 100 proporcionado por DACPOL SP. ZOO.

Resumen

La mayoría de los métodos de localización de ondas de falla se basan en el análisis de la corriente de línea transformada por transformadores de corriente y se limitan a redes de alta tensión. La localización de ondas de falla en redes de media tensión aún está en desarrollo. Este artículo presenta un nuevo algoritmo en tiempo real para la identificación de ondas viajeras en una red de distribución usando señal de voltaje y el método de lápiz de matriz de tiempo corto. Para obtener las formas de onda de voltaje del lado secundario en la subestación, se desarrolló el modelo de un sensor de voltaje resistivo basado en las medidas de banda ancha de 10 Hz a 20 MHz. El sensor probado amplifica las frecuencias asociadas con las ondas viajeras más que la frecuencia de la red, lo que permite la identificación. Se realizaron simulaciones de cortocircuito en el alimentador de bus IEEE 34 para probar el algoritmo. El método desarrollado puede detectar incluso las ondas de baja amplitud.

1. Introducción

Proteger el sistema de potencia de fallas es uno de los objetivos de los relés de protección. La eliminación rápida de perturbaciones limita el daño infligido a los equipos eléctricos y reduce su impacto negativo en la calidad de la energía eléctrica. Por lo tanto, el desarrollo de relés y localizadores de fallas rápidos y precisos en las redes de distribución es un tema clave tanto desde el punto de vista técnico como económico. En el caso de redes de alta tensión, la localización de fallas es fácil ya que se caracterizan por una gran dispersión de medidas y estructura de bucle. En el caso de las redes de distribución, las mediciones se realizan principalmente en un solo punto de la subestación allí. Además, las redes de distribución tienen una estructura de árbol, lo que hace que la identificación de la rama fallada sea incierta. La solución a este problema puede ser el uso de localizadores de ondas viajeras, que en este caso pueden ser más precisos que los métodos convencionales. Para hacer posible el uso de dichos localizadores, es necesario desarrollar los métodos más precisos de identificación de ondas viajeras.

El enfoque convencional para la detección de fallas se basa en el análisis de corrientes y voltajes de una frecuencia fundamental. Por este motivo, los algoritmos de protección basados en este tipo de señales requieren el análisis de un intervalo de señal lo suficientemente largo como para asegurar que se ha producido la perturbación. Un enfoque más moderno se basa en ondas viajeras, que son señales de mayor frecuencia que se propagan a lo largo de las líneas eléctricas. Este tipo de protección a veces se denomina "velocidad ultraalta". Detecta ondas de corriente y tensión generadas por faltas. Luego, esta protección determina tanto el tipo como la ubicación de la perturbación en base a la comparación de sus amplitudes y tiempos de llegada a los dispositivos de medición. Sin duda, la principal ventaja de la protección basada en ondas es la velocidad de funcionamiento (menos de 4 ms) [1]. Además, funciona correctamente con líneas de transmisión compensadas en serie y durante oscilaciones de potencia.

La localización de fallas mediante ondas viajeras se puede dividir en esquemas de dos terminales y de una sola terminal. En el caso de relés de doble terminal, la adquisición de datos de medición ocurre en los extremos de las líneas protegidas y requiere la transmisión de datos de medición entre dispositivos. Sin embargo, los relés de un solo terminal analizan las señales de corrientes y voltajes desde un solo punto de medición. Cabe destacar que los relés de dos terminales se caracterizan por una mayor confiabilidad porque utilizan ondas generadas directamente por la perturbación para localizarla y clasificarla. Estas ondas tienen la mayor amplitud posible y se detectan primero después de una falla. Sin embargo, en el caso de los relés de un solo terminal, la protección se basa en la onda generada por la perturbación y en las ondas reflejadas por las discontinuidades de la línea, los ramales y la falla misma [2]. Se debe a la falta de un segundo punto de medición en la red.

Las redes de alta tensión se caracterizan por la presencia de subestaciones con equipos de medida en los extremos de línea. Por lo tanto, aquí se utilizan relés de dos terminales. En el caso de las redes de distribución, las subestaciones de alta/media tensión suelen ser el único lugar donde se colocan los relés de protección con transformadores o sensores. Esto significa que en las redes de distribución el uso de relés de onda de un solo extremo es la solución más económica.

Las redes de distribución son las redes con una topología de árbol, y esta característica dificulta la ubicación precisa de fallas. Tanto para los localizadores de fallas convencionales como para los de onda, la situación es más complicada que en las redes de transmisión, ya que pueden existir varios ramales potenciales con fallas a una distancia conocida de la subestación. Solo una de las ramas está fallada. Sin embargo, se puede determinar una línea en cortocircuito comparando las amplitudes de las ondas de corriente dispersas en los buses de la subestación [2,3,4].

Se han propuesto diferentes métodos de localización de fallas, como la detección de frecuencias asociadas a oscilaciones de ondas entre nodos [5], comparación de la corriente medida con la predicha para una ubicación de cortocircuito determinada [6] y métodos más tradicionales basados en la detección de frentes de onda de falla [3,7]. Se han utilizado los siguientes métodos para detectar frentes de onda: transformada wavelet, análisis de componentes principales basado en extracción de características, operador de energía de Teager, descomposición de modo empírico de conjuntos y el método del lápiz de matriz, que se analiza y utiliza en este documento [8,9]. El método del lápiz de matriz se usa para descomponer una señal en la suma de sinusoides amortiguados exponencialmente [10]. En el campo de la ingeniería de energía eléctrica, el método del lápiz matricial se ha utilizado para estimar los modos fundamentales de oscilaciones debido a fallas y para estimar armónicos y subarmónicos [11,12,13].

Las señales eléctricas procesadas por algoritmos de procesamiento de datos digitales se entregan al relé por medio de dispositivos de medición ubicados en la estación. Estos dispositivos incluyen transformadores de corriente y voltaje, bobinas de Rogowski o sensores que reducen el nivel de las señales eléctricas al nivel aceptable por los relés. Es importante que la señal en el lado secundario de estos dispositivos se reproduzca con la mayor precisión posible e, idealmente, solo debe escalarse. En la práctica, sin embargo, los instrumentos de medición tienen una ganancia y un cambio de fase variables según la frecuencia de la señal. El instrumento no debe atenuar demasiado las frecuencias altas para poder detectar una onda viajera entrante, que es una forma de onda que cambia rápidamente y, por lo tanto, contiene componentes de alta frecuencia. Debe enfatizarse que para reproducir con precisión la amplitud de la onda de falla, el instrumento debe introducir un retardo de tiempo constante (preferiblemente ninguno) y sus características de amplificación deben ser lo menos variables posible.

Los transformadores son los instrumentos que tradicionalmente se utilizan en la industria de la energía eléctrica para medir el voltaje. Se caracterizan por una transformación muy precisa de las señales eléctricas, pero también presentan inconvenientes. Contribuyen al fenómeno negativo de la ferroresonancia, están expuestos a daños causados por cortocircuitos en el circuito secundario y no son capaces de transformar componentes de tensión de alta frecuencia (>3 kHz) con precisión [14]. Es por ello que, como respuesta a la necesidad de medir con precisión los componentes transitorios, se han desarrollado sensores no convencionales basados en mecanismos distintos al sistema transformador [15,16].

Para mediciones de voltaje, los sensores de voltaje basados en divisores capacitivos (C), resistivos (R) y resistivos-capacitivos (RC) son sensores no convencionales populares [14]. En particular, los divisores R y RC son los más populares ya que no pueden inducir ferrorresonancia debido a una inductancia insignificante, transforman los transitorios y las altas frecuencias con precisión, lo que permite la descarga de la carga acumulada en la línea y son resistentes a los cortocircuitos del lado secundario. Estos divisores se pueden utilizar con éxito para medir la calidad de la energía y para la localización de cortocircuitos mediante fenómenos ondulatorios.

La literatura sobre el modelado de transformadores convencionales es muy amplia pero, lamentablemente, suele referirse a la descripción de sus características a frecuencias inferiores a 10 kHz [15,17]. Además, los autores no han podido encontrar los datos numéricos de los diagramas de Bode o las funciones de transferencia de los transformadores de tensión (tanto convencionales como no convencionales) hasta 1 MHz incluso en los artículos que describen los estudios en este campo [18,19]. Dichos datos están disponibles para un transformador de corriente convencional [20]. Por supuesto, los sensores difieren en el diseño, lo que lleva a variaciones en sus características de transferencia de un tipo a otro, pero parece necesario conocer la función de transferencia de un ejemplo.

Para obtener tales datos, se realizaron mediciones de las características de frecuencia de un sensor de media tensión. Luego, se utilizaron para desarrollar su modelo de función de transferencia. A continuación, se presentó el método de lápiz de matriz de corta duración mejorado en aplicación a la detección de ondas de cortocircuito de tensión en la red de media tensión medidas en el lado secundario de los sensores de tensión.

La estructura del artículo es la siguiente. La Sección 2 proporciona una descripción del método de lápiz de matriz de tiempo corto con su aplicación para encontrar pulsos de señal. También se proporciona el algoritmo para la identificación de los pulsos. La Sección 3 contiene los resultados de la medición de la función de transferencia del sensor de voltaje y los resultados de la operación del algoritmo sobre la base de simulaciones realizadas. Las conclusiones se dan en la Sección 4.

2. La Identificación de Impulsos de Falta en una Red de Media Tensión

2.1. El método de lápiz de matriz de tiempo corto

El método de lápiz de matriz de tiempo corto (STMPM) aproxima una señal dentro de la ventana que se mueve con el tiempo como la suma de componentes sinusoidales con una amplitud exponencialmente variable [21]:

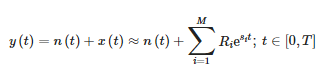
dónde:

• y(t): señal de medición,
• n(t)—ruido,
• x(t)—señal original,
• Ri: residuos o amplitudes complejas de componentes,
• Si: polos complejos y
• M: número de componentes de aproximación.

Para una señal muestreada t = kT_s, la ecuación anterior toma la siguiente forma:

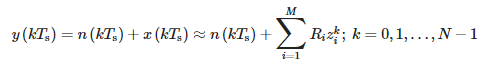
dónde:

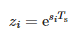
• Ts—período de muestreo y
• N: número de muestras.

Para determinar los parámetros de aproximación se construirá la siguiente matriz:

Aquí, L es un parámetro de lápiz. El número de componentes de aproximación M satisface la siguiente relación:

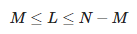
Así, vemos que el valor máximo de M es igual a ⌊N/2⌋.
Sometiendo la matriz Y a descomposición en valores singulares (SVD) obtenemos:

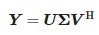
dónde:

• U: matriz unitaria de tamaño (N − L) × (N − L),
• Σ: matriz diagonal rectangular de valores singulares con un tamaño de (N − L) × (L + 1) y
• V: matriz unitaria de tamaño (L + 1) × (L + 1).

Si la señal medida no contuviera ruido, la matriz Σ contendría exactamente M distinto de cero singular valores. Debido al ruido, los valores singulares pueden distorsionarse, lo que se manifiesta por pequeños valores singulares adicionales. El efecto de ruido se elimina eliminando estos pequeños valores. Solo quedan valores dominantes M que cumplan la siguiente condición:

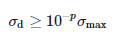
donde σ_max es un valor singular dominante y p es el número de dígitos decimales significativos precisos de medición.

Luego se construyen submatrices de las matrices SVD resultantes:

1. La matriz U′=[u1,u2,…,u_M] de tamaño (N − L) × M se crea dejando las columnas correspondientes a los valores singulares que satisfacen la Condición (7) y eliminando los demás;
2. La matriz diagonal cuadrada Σ=diag(σ1,σ2,…,σM) se forma eliminando las columnas y filas de la matriz Σ, que contienen valores singulares que no satisfacen la Condición (7);
3. La matriz V′=[v1,v2,…,v_M] de tamaño (L + 1) × M se forma dejando las columnas correspondientes a los valores singulares que satisfacen la Condición (7) y eliminando los demás.

Luego, la matriz V₁′ se crea eliminando la última fila de la matriz V′. V₂′ se construye eliminando la primera fila de la matriz V′.

Luego, se calculan las siguientes matrices:

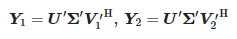
Los valores zi son valores propios generalizados distintos de cero del par de matrices (Y₁, Y₂), es decir, valores propios de Y ^†₁Y₂, donde Y^†₁ es la pseudoinversa de Moore-Penrose de Y₁. Luego calculamos los polos:

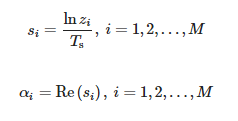
Los valores de las amplitudes se pueden determinar de la siguiente manera:

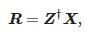
dónde:

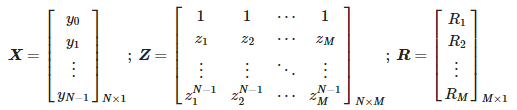
Las operaciones anteriores se realizan en el método de lápiz de matriz de tiempo corto para intervalos de datos sucesivos [22].

Los resultados aproximados de los valores propios, las pseudoinversiones y los algoritmos SVD pueden afectar la aparición de valores zi distintos de cero aunque cercanos a cero. Estos valores afectan la velocidad de MPM y pueden afectar negativamente sus resultados, por lo que vale la pena eliminarlos antes de calcular los residuos.

2.2. El Comportamiento de los Polos Componentes en la Vecindad de un Pulso

Las fallas en la red eléctrica generan pulsos que se propagan a lo largo de las líneas eléctricas a velocidades cercanas a la velocidad de la luz [3]. Estos impulsos se pueden identificar mediante el análisis de cambio de polos de la aproximación STMPM. La figura 1 muestra tres ejemplos de pulsos de forma gaussiana y los polos de su aproximación con STMPM. Cuando llega el pulso, la aproximación con componentes exponenciales cambia a medida que se mueve la ventana de tiempo. Cuando el pulso está a la derecha del punto medio de la ventana los polos de la aproximación tienen una parte real positiva, cuando el vértice gaussiano está en el medio de la ventana la parte real de los polos es cercana a cero, y cuando el el pulso esta en la primera mitad de la ventana los polos tienen parte real negativa. El cambio de signo de la parte real de los polos indica por tanto que el centro del pulso ha pasado por el punto medio de la ventana de muestreo [9,22]. También podemos ver en la Figura 2 que los polos con el valor absoluto más grande de la parte real (y por lo tanto con la tasa de cambio de amplitud más rápida) tienen el valor más grande del módulo de amplitud inicial (residuo).

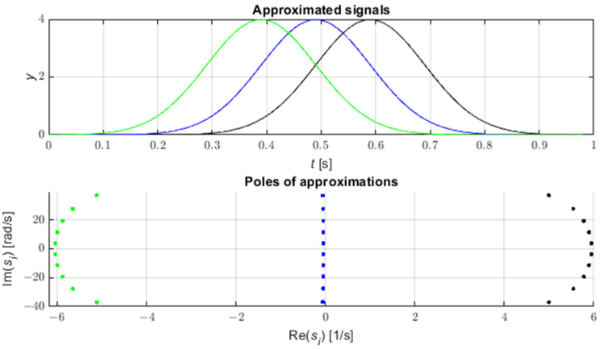
Figura 1. Gaussianas y polos de aproximación correspondientes.

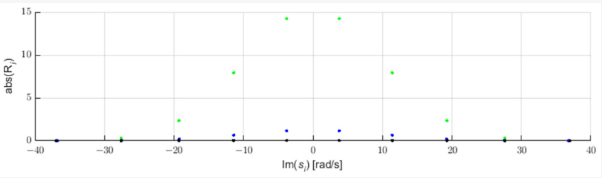
Figura 2. Residuos de componentes de aproximaciones gaussianas.

Así, vemos que la coordenada de tiempo del pico del pulso se puede identificar aproximadamente con el momento de cambio de signo de los coeficientes de amortiguamiento.

Al obtener el curso dependiente del tiempo de estos coeficientes con el uso de STMPM, podemos someterlos a una aproximación lineal en la vecindad del punto donde los coeficientes pasan por cero y obtener una coordenada máxima aproximada del pulso. Cabe señalar que los coeficientes caracterizados por la mayor variabilidad también se caracterizan por la mayor amplitud: son los componentes más grandes del pulso.

2.3. El algoritmo de detección de pulso en tiempo real

El diagrama de flujo del algoritmo para la detección de impulsos que se originan en ondas viajeras se presenta en la Figura 3. El algoritmo somete ventanas sucesivas de la señal a STMPM para extraer tasas de decaimiento de los componentes de aproximación.

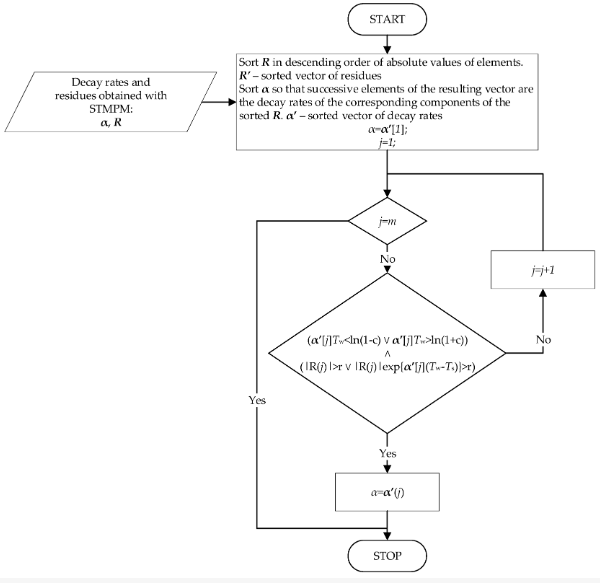
Figura 3. El algoritmo de selección de tasas de decaimiento.

Los componentes obtenidos se someten a selección, cuyo procedimiento se presenta en la Figura 4. La selección se basa en el supuesto de que aquellos componentes del STMPM, que se caracterizan por la mayor amplitud, deben tomarse para el tiempo pico aproximación: constituyen la mayor contribución a la componente transitoria de la señal. Esto está de acuerdo con la observación del punto anterior: los componentes con la mayor variación de amplitud se caracterizan por la mayor amplitud inicial. En el caso de que el componente con la mayor amplitud se caracterice por una pequeña tasa de caída durante toda la ventana de longitud T_w—menor que el parámetro c—o su contribución máxima a la señal sea menor que r, el siguiente componente en términos de magnitud de amplitud se selecciona como candidato potencial para la tasa de decaimiento α. Repitiendo este procedimiento para los componentes posteriores hasta que se cumpla la condición, finalmente se obtiene el coeficiente α que se utiliza entonces para aproximar el tiempo de llegada del pulso. Si ninguna de las componentes cumple las condiciones anteriores, se selecciona la de mayor amplitud.

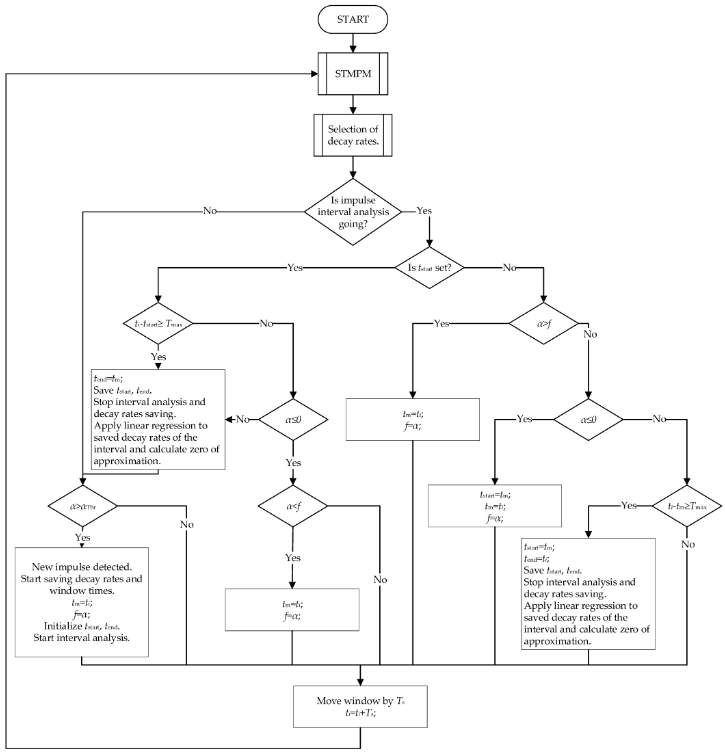
Figura 4. El algoritmo de identificación de pulsos.

Se considera que el tiempo asociado a una ventana es:

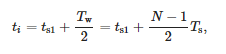
donde t_s1—hora de la muestra de la primera ventana y T_w—ancho de la ventana.

La llegada de un pulso se indica mediante un fuerte aumento en las tasas α asociado con un cambio rápido de la señal al final de la ventana de muestreo. El parámetro α_Thr se selecciona como el umbral de las tasas de caída. Cuando se excede el umbral de detección, los valores subsiguientes de los coeficientes α y los tiempos de ventana se escriben en la memoria y se inicia el análisis de datos para determinar límites de pulso más precisos. El momento en que t_comienza con el valor más alto de α antes de cambiar el signo de la tasa de decaimiento se selecciona como el inicio adecuado del pulso. Para almacenar los tiempos potenciales de los límites de pulso correctos, se introdujo la variable t_m con la variable f que contiene los valores más grandes de α del pulso calculado hasta el momento.

Si se encuentra el valor de t_inicio, comienza la búsqueda del final propio del pulso t_fin. Esto corresponde al valor más pequeño de α antes de que el signo cambie nuevamente, esta vez al positivo. La variable i_m se utiliza de nuevo para almacenar los puntos finales potenciales anteriores. La variable f contiene los valores α mínimos anteriores.

Cuando la longitud del pulso es igual a la T_max de las muestras o se encuentra el final del pulso, el análisis del pulso finaliza.

Función α(t) en el intervalo [t_inicio; t_end] se somete a una regresión lineal. Los coeficientes de esta regresión se encuentran como la solución al siguiente problema:

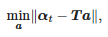
donde: α_t=[α(t_inicio),α(t_inicio+Ts),…,α(t_final)]^T, a=[a₁,a₀]^T

Los coeficientes buscados son:

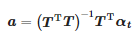
Mientras que el momento de llegada del impulso es:

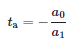
2.4. El alimentador de prueba de 34 buses IEEE adaptado

Para los cálculos de cortocircuito, se creó un modelo de alimentador de prueba IEEE de 34 buses en Simulink. La topología del alimentador se muestra en la Figura 5 [23]. El alimentador se basa en una red real en el estado de Arizona. Es lo suficientemente simple como para no convertirse en una carga computacional sustancial durante las simulaciones transitorias con un pequeño paso de integración. Se simplificó el modelo y se cambiaron los parámetros para imitar las cuadrículas europeas:

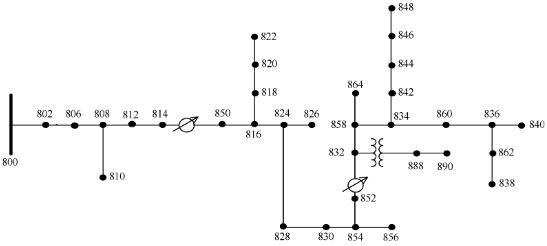
Figura 5. La topología del alimentador de 34 buses IEEE.

• Se cambió el voltaje de la red de 24,9 kV a 16,5 kV;
• Se supuso que todas las secciones de las líneas eléctricas eran líneas aéreas con los mismos parámetros;
• Se quitaron los reguladores de voltaje;
• Se asumió que las cargas distribuidas estaban agrupadas en autobuses en el extremo más alejado de las líneas cargadas;
• Las cargas se conectaron a la red de media tensión a través de transformadores de distribución;
• El punto neutro del transformador de alta/media tensión se desconectó de la conexión a tierra.

Parámetros de la fuente de tensión:

• frecuencia de 50 Hz;
• voltaje de línea de 115,5 kV;
• Resistencia 0,00227 Ω.
• Fuente simétrica con desfase de fase L1 igual a 0°.

Parámetros del transformador de potencia:

• Relación de tensión 115,5/16,5;
• Grupo de vectores de devanado de alta tensión Yg;
• Grupo de vectores de bobinado de baja tensión D11;
• Potencia 6,3 MVA;
• Tensión de cortocircuito relativa 7,5 %;
• Resistencia de cortocircuito igual al 0,49 % de la impedancia equivalente.

Parámetros de los transformadores de distribución:

• Relación de tensión 15,75/0,4;
• Grupo de vectores de bobinado de alta tensión D11;
• Grupo de vectores de bobinado de baja tensión Yg;
• Potencia 630 kVA;
• Tensión de cortocircuito relativa 6 %;
• Resistencia de cortocircuito igual al 17,2 % de la impedancia equivalente.

Parámetros de líneas eléctricas:

• Línea trifásica sin neutro;
• Un conductor por fase;
• Diámetro del conductor 0,8466 cm;
• Relación T/D 0,311;
• Resistencia CC 0,5939 Ω/km;
• Posiciones horizontales de los conductores x=[−1.05, 0, 1.05];
• Posiciones verticales de los conductores u=[−9.05, 10.61, 9.05];
• Resistividad del terreno ρ=100 Ωm.

Se adjuntaron capacitancias a cada transformador como se muestra en la Figura 6 [5] en para modelar las propiedades de los transformadores a altas frecuencias.

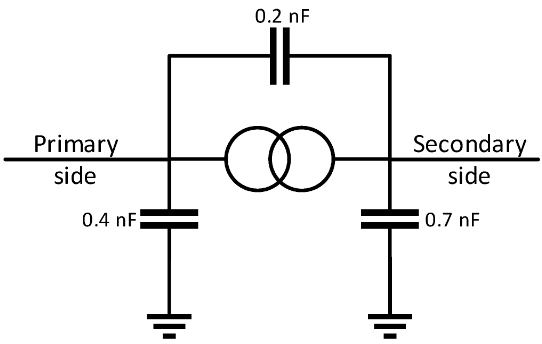
Figura 6. Modelo de transformador.

Las líneas eléctricas se modelaron entre 1 Hz y 1 MHz teniendo en cuenta el efecto de piel utilizando el modelo de línea universal.

Se realizaron simulaciones de cortocircuitos monofásicos y multifásicos con resistencia de cruce por cero al 20 %, 50 %, 80 % y 100 % de longitud de las líneas. Corresponde a 76 lugares de cortocircuito. El paso de integración de la simulación fue Δt=0.1 μs. Tustin/Backward Euler fue el método de integración utilizado.

3. Resultados

3.1. Mediciones de las Características de Transmisión del Sensor de Media Tensión

Las mediciones de la respuesta de frecuencia se realizaron para un sensor de media tensión destinado a montarse en cabezales de conectores. El sensor era un divisor resistivo con una tensión primaria nominal de 20/√3 kV y una tensión secundaria nominal de 3,25/√3, que corresponde a la relación de tensión de:

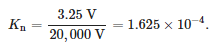
Para las mediciones se utilizó el analizador vectorial de redes Bode 100 de OMICRON Lab. Este dispositivo hace posibles las mediciones en el rango de 1 Hz a 50 MHz. Para realizar las pruebas se utilizó la función de medición de ganancia y fase del dispositivo. Esta función se basó en la comparación de la amplitud y la fase de las señales de voltaje en los lados primario y secundario del sensor. La medición de la función de transferencia, definida como la relación entre el voltaje en el lado secundario y el voltaje en el lado primario, se realizó para 2048 valores de frecuencia en el rango de 10 Hz a 20 MHz. Los valores medidos se presentan en la Figura 7.

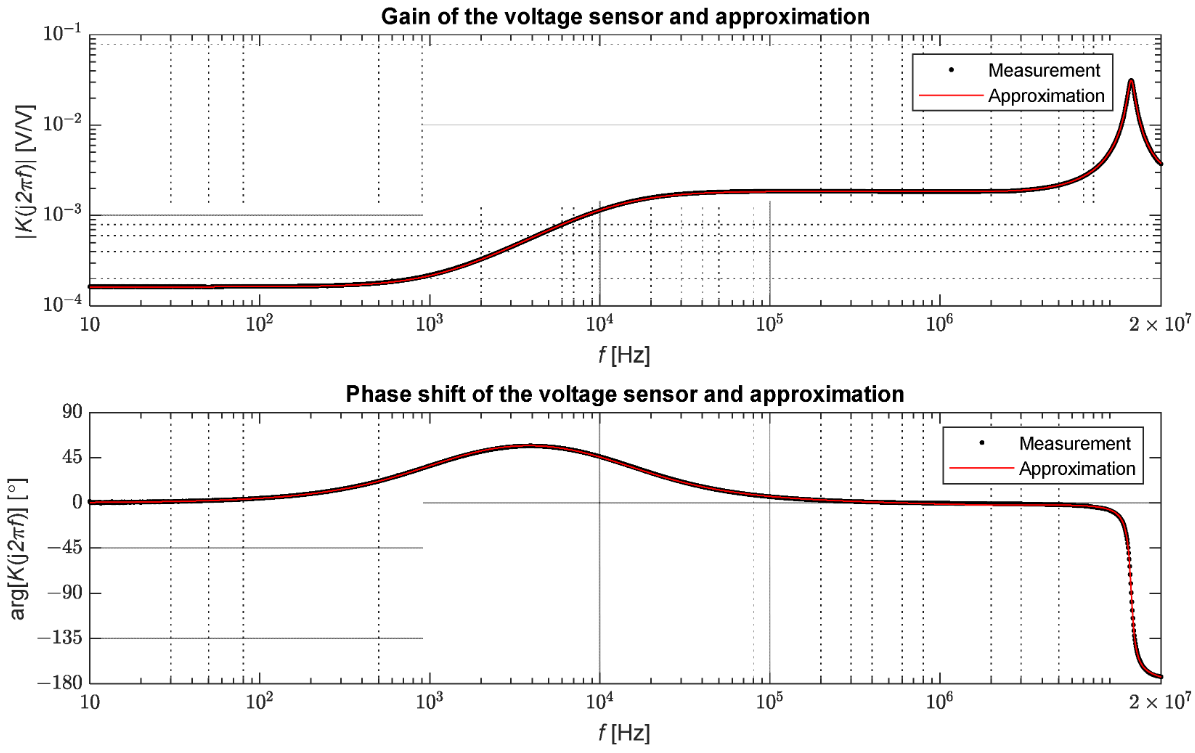
Figura 7. Resultados de la medición de la transmitancia del sensor de media tensión.

El sensor de voltaje probado mantiene un coeficiente de transferencia nominal para señales de hasta una frecuencia de aproximadamente 1 kHz, luego el gráfico aumenta al nivel de ganancia de aproximadamente 1,84 × 10⁻³; este nivel se mantiene entre aproximadamente 12,5 kHz y 6,6 MHz. Debido a la propiedad diferenciadora del sensor, aquí hay un cambio de fase positivo de aproximadamente 57° en la zona de transición de 100 Hz a 100 kHz. En el caso de la fase, podemos distinguir dos zonas para las que el desfase no supera los 6°. En este caso, el rango de frecuencia es de hasta aproximadamente 130 Hz y de 105 kHz a 9,4 MHz. Por lo tanto, se puede concluir que en el rango de 105 kHz a 6,6 MHz, las señales se transforman proporcionalmente pero con un factor de proporcionalidad diferente que cerca de la frecuencia de la red. En el caso de los fenómenos de las olas, este rango es suficiente para representar con precisión la forma de las ondas que se propagan en una cuadrícula [20]. Vale la pena señalar que los sensores de voltaje con diferentes construcciones pueden exhibir diferentes propiedades de transferencia.

Para desarrollar un modelo matemático del sensor, se utilizó la función “tfest” de MATLAB para aproximar los datos obtenidos mediante una función de transferencia estable de la siguiente forma:

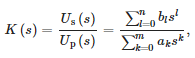
dónde:

• Up(s): voltaje en el lado primario del sensor,
• Us(s): voltaje en el lado secundario del sensor,
• n: el orden del numerador,
• m —el orden del denominador y
• ak, bl —coeficientes de polinomios del denominador y numerador de la transmitancia, sucesivamente.

Los valores de los coeficientes de la función de transferencia se presentan en la Tabla 1. Vale la pena señalar que la transmitancia modelada es adecuada ya que el orden del denominador es mayor que el orden del numerador. La Figura 7 también presenta la comparación de las funciones de transferencia obtenidas de las mediciones con la aproximación por la Fórmula (19). También se calculó el error cuadrático medio entre los puntos de medición y la aproximación determinada por la siguiente relación:

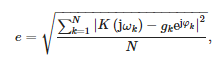
dónde:

• N = 2048: número de frecuencias de medición
• g_k —ganancia medida del sensor en la pulsación ω_k y
• φ_k : cambio de fase medido del sensor en la pulsación ω_k.

El valor del error de aproximación es igual a:

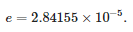
Tabla 1. Valores de los coeficientes polinómicos de la transmitancia equivalente de un sensor de tensión con estructura divisoria resistiva.

La Figura 8 muestra la comparación de la forma de onda de tensión de fase en la subestación obtenida de la simulación y la tensión en la salida del sensor modelado en el caso de un cortocircuito trifásico directo a tierra en el nodo 816. Es claramente visible que la amplificación de los transitorios rápidos es mayor que la de los transitorios lentos. Vale la pena señalar que estas formas de onda se amplifican casi proporcionalmente.

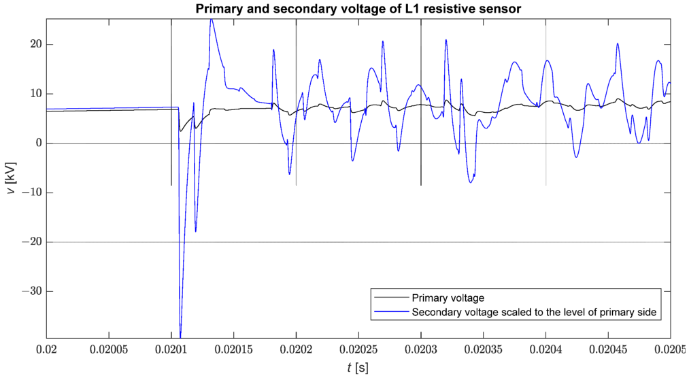
Figura 8. Comparación de la forma de onda del voltaje de fase (v_L1) y el voltaje en la salida del sensor escalado al voltaje primario (v_L1/K_n) durante la falla.

3.2. La identificación de impulsos de cortocircuito utilizando STMPM

La Figura 9 muestra la forma de onda de todas las tasas de caída de una forma de onda de voltaje de ejemplo en una subestación después de un cortocircuito trifásico de impedancia cero a tierra en el nodo 816 del modelo. Puede verse que la falta de selección de velocidades de decaimiento hace que los pulsos sean difíciles de localizar; esto es particularmente cierto para los pulsos más débiles. Por otro lado, la observación visual de las tasas de decaimiento permite identificar fácilmente los intervalos que contienen pulsos en el caso del análisis visual de formas de onda de tensión de fase, aunque esto no siempre es fácil en el caso de amplitudes de pulso pequeñas.

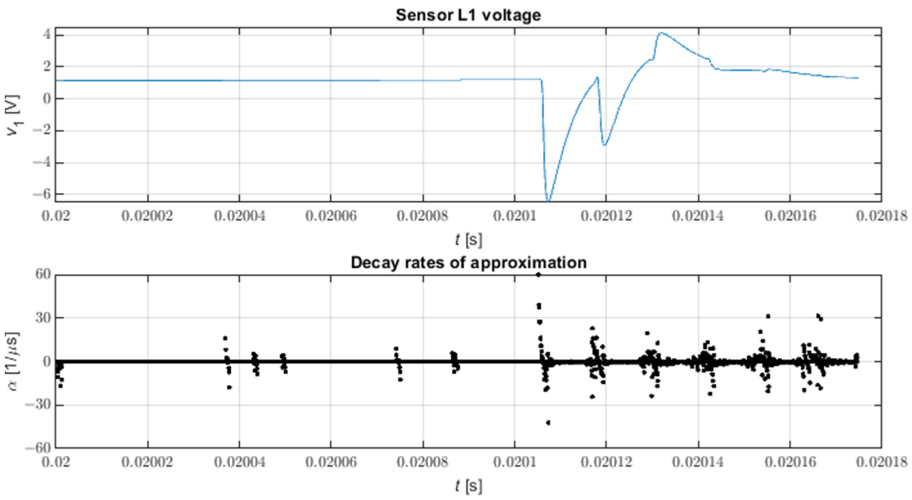
Figura 9. Todas las tasas de descomposición de la aproximación STMPM. N = 9, L = 4.

La figura 10 muestra las tasas de disminución seleccionadas junto con la regresión lineal utilizada para identificar el momento de llegada del pulso. El número de detecciones de pulsos falsos se puede reducir filtrando los coeficientes de atenuación innecesarios.

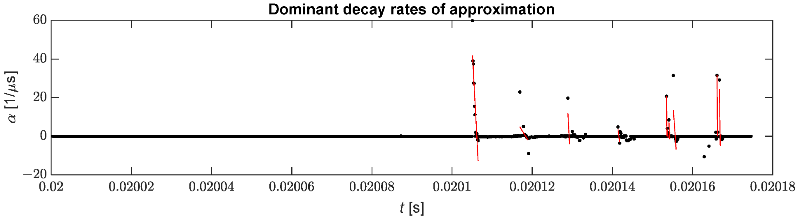
Figura 10. Tasas de decaimiento seleccionadas utilizadas para la identificación de pulsos.

La tabla 2 muestra los errores al identificar la hora de llegada de la primera ola entrante a la estación. Este error se define mediante la siguiente ecuación:

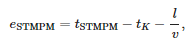
dónde:

• t_STMPM —momento de llegada según STMPM,
• t_K —momento de falla,
• l — distancia de la ubicación del cortocircuito desde la subestación y
• v = 299 552 300 m/s: velocidad de propagación de las ondas de falla medida para un cortocircuito en el nodo más lejano (838).

Los parámetros del método utilizados para obtener los resultados son:

• N = 5: número de muestras por ventana de tiempo;
• L = 2: parámetro de lápiz;
• p = 6: el número de dígitos decimales significativos precisos de medición;
• α_Thr=1051s —umbral de detección de pulso;
• T_max=2.1 μs —ancho de pulso máximo;
• T_w=0.5 μs —ancho de ventana;
• T_s=0,1 μs —período de muestreo;
• r=0,02 V —umbral de amplitud.

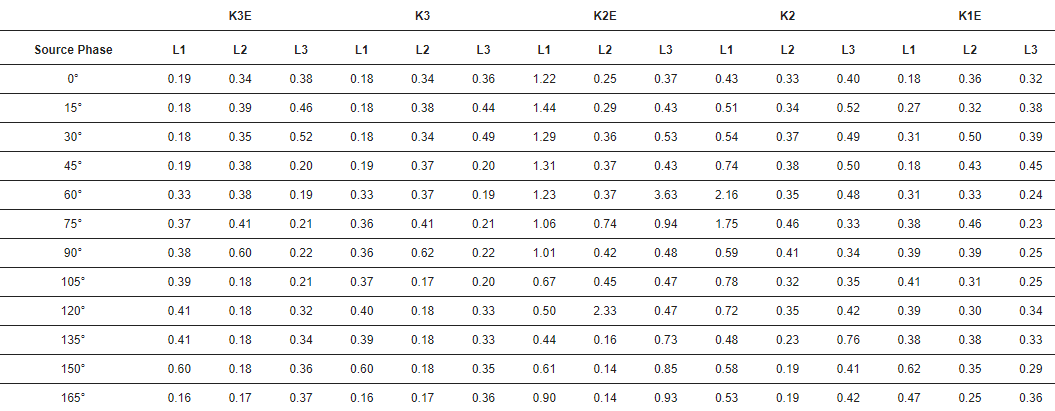
La tabla 3 muestra las desviaciones estándar del error temporal del pulso.

Tabla 2. Error temporal de identificación de onda en caso de diferentes faltas. Unidad: µs. K3E: falla trifásica a tierra, K3: falla trifásica, K2E: falla bifásica a tierra, K2: falla bifásica, K1E: falla de fase a tierra.

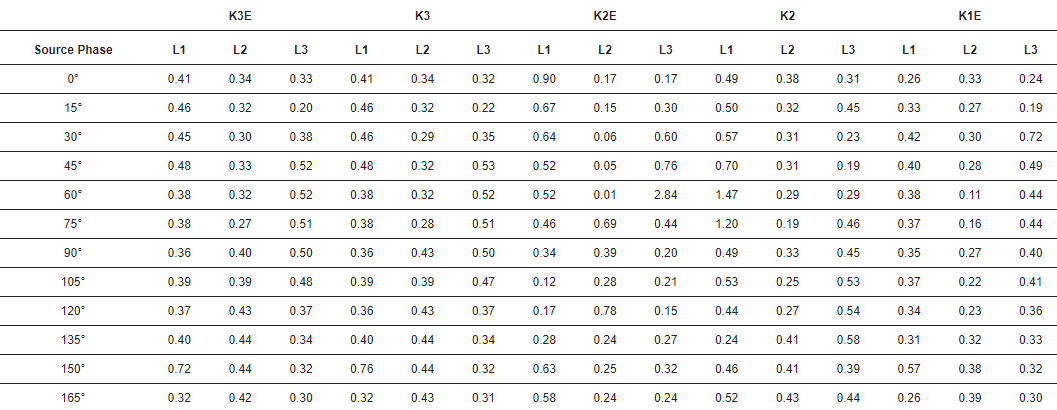
Tabla 3. Desviación estándar del error temporal. Unidad: µs. K3E: falla trifásica a tierra, K3: falla trifásica, K2E: falla bifásica a tierra, K2: falla bifásica, K1E: falla de fase a tierra.

4. Discusión

Se desarrolló el modelo de función de transferencia de un sensor de voltaje resistivo basado en las mediciones de banda ancha de 10 Hz a 20 MHz. Las simulaciones de ondas viajeras generadas por fallas en el modelo de 34 buses IEEE se realizaron utilizando la función de transferencia. La respuesta de frecuencia del sensor resistivo fue suficiente para la identificación de ondas de falla en la señal de voltaje secundario. El sensor transforma las señales de ondas viajeras con una ganancia aproximadamente constante, que es mayor que la ganancia en la frecuencia de la red pública. Para la identificación se utilizó un nuevo algoritmo en tiempo real basado en el método del lápiz matricial. La variación de este método utilizada en el trabajo se caracteriza por la alta precisión en la identificación de ondas, ya que el error promedio fue de 0.41 µs en el muestreo de 10 MHz, y el error tuvo un valor positivo por lo que el tiempo de llegada encontrado fue mayor al real. Sin embargo, cabe señalar que en las aplicaciones prácticas del método, por ejemplo, en la localización de fallas por ondas, la parte de este error se elimina debido a la operación diferencial de estos algoritmos. La identificación precisa de las ondas de falla puede permitir clasificar y localizar fallas en redes de media tensión utilizando barras colectoras como único punto de medición. Se requiere una prueba con señales reales para verificar la efectividad del algoritmo y compararlo con otros métodos para identificar pulsos de onda entrantes. Una transformación de voltaje bastante correcta por parte de los sensores puede permitir la clasificación del tipo de falla en función de las amplitudes de las ondas generadas por ellos.

Referencias

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).