L'identification des ondes progressives dans un signal de capteur de tension dans un réseau moyenne tension à l'aide de la méthode du crayon matriciel à court terme

L'analyseur de circuit vectoriel Omicron-Lab Bode 100 fourni par DACPOL SP a été utilisé dans les tests. ZOO.

Résumé

La plupart des méthodes de localisation des ondes de défaut sont basées sur l'analyse du courant de ligne transformé par les transformateurs de courant et sont limitées aux réseaux à haute tension. La localisation des ondes de défaut dans les réseaux moyenne tension est encore en cours de développement. Cet article présente un nouvel algorithme en temps réel pour l'identification des ondes progressives dans un réseau de distribution à l'aide d'un signal de tension et de la méthode du crayon matriciel à court terme. Pour obtenir les formes d'onde de tension côté secondaire à la sous-station, le modèle d'un capteur de tension résistif basé sur les mesures à large bande de 10 Hz à 20 MHz a été développé. Le capteur testé amplifie les fréquences associées aux ondes progressives plus que la fréquence d'utilité permettant l'identification. Des simulations de court-circuit sur le chargeur de bus IEEE 34 ont été effectuées pour tester l'algorithme. La méthode développée peut détecter même les ondes de faible amplitude.

1. Présentation

Protéger le système électrique contre les défauts est l'un des objectifs du relais de protection. L'élimination rapide des perturbations limite les dommages infligés aux équipements électriques et réduit leur impact négatif sur la qualité de l'énergie électrique. Par conséquent, le développement de relais et de localisateurs de défauts rapides et précis dans les réseaux de distribution est un enjeu clé tant d'un point de vue technique qu'économique. Dans le cas des réseaux à haute tension, la localisation des défauts est facile car ils se caractérisent par une grande dispersion des mesures et de la structure de boucle. Dans le cas des réseaux de distribution, les mesures sont principalement effectuées en un seul point de la sous-station. De plus, les réseaux de distribution ont une structure arborescente, ce qui rend incertaine l'identification des branches défaillantes. La solution à ce problème peut être l'utilisation de localisateurs à ondes progressives, qui dans ce cas peuvent être plus précis que les méthodes conventionnelles. Afin de rendre possible l'utilisation de tels localisateurs, il est nécessaire de développer les méthodes les plus précises d'identification des ondes progressives.

L'approche conventionnelle de la détection des défauts est basée sur l'analyse des courants et des tensions d'une fréquence fondamentale. Pour cette raison, les algorithmes de protection basés sur ces types de signaux nécessitent l'analyse d'un intervalle de signal suffisamment long pour s'assurer que la perturbation s'est produite. Une approche plus moderne est basée sur les ondes progressives, qui sont des signaux de fréquence plus élevée se propageant le long des lignes électriques. Ce type de protection est parfois appelé « ultra-haut débit ». Il détecte les ondes de courant et de tension générées par les défauts. Ensuite, cette protection détermine à la fois le type et la localisation de la perturbation sur la base de la comparaison de leurs amplitudes et temps d'arrivée aux appareils de mesure. Sans aucun doute, le principal avantage de la protection basée sur les ondes est la rapidité de fonctionnement (moins de 4 ms) [1]. De plus, il fonctionne correctement avec les lignes de transmission compensées en série et lors des oscillations de puissance.

La localisation des défauts à l'aide d'ondes progressives peut être divisée en schémas à deux terminaux et à un seul terminal. Dans le cas de relais à double borne, l'acquisition des données de mesure se produit aux extrémités des lignes protégées et nécessite la transmission des données de mesure entre les appareils. Cependant, les relais à borne unique analysent les signaux de courants et de tensions à partir d'un seul point de mesure. Il convient de souligner que les relais à deux bornes se caractérisent par une plus grande fiabilité car ils utilisent des ondes directement générées par la perturbation pour la localiser et la classer. Ces ondes ont la plus grande amplitude possible et sont détectées en premier après un défaut. Cependant, dans le cas des relais à borne unique, la protection est basée sur l'onde générée par la perturbation et sur les ondes réfléchies par les discontinuités de ligne, les branches et le défaut lui-même [2]. Cela est dû à l'absence d'un deuxième point de mesure dans le réseau.

Les réseaux à haute tension se caractérisent par la présence de sous-stations avec des équipements de comptage aux extrémités des lignes. Des relais à double borne sont donc utilisés ici. Dans le cas des réseaux de distribution, les sous-stations haute/moyenne tension sont généralement le seul endroit où sont placés les relais de protection avec transformateurs ou capteurs. Cela signifie que dans les réseaux de distribution, l'utilisation de relais d'onde asymétriques est la solution la moins chère.

Les réseaux de distribution sont les réseaux avec une topologie arborescente, et cette fonctionnalité rend difficile la localisation précise des défauts. Pour les localisateurs de défauts conventionnels et par ondes, la situation est plus compliquée que dans les réseaux de transmission, car plusieurs branches potentiellement défaillantes peuvent exister à une distance connue de la sous-station. Une seule des branches est faillée. Cependant, une ligne en court-circuit peut être déterminée en comparant les amplitudes des ondes de courant diffusées sur les bus de la sous-station [2,3,4].

Différentes méthodes de localisation des défauts ont été proposées, telles que la détection des fréquences associées aux oscillations des ondes entre les nœuds [5], comparaison du courant mesuré avec celui prévu pour un emplacement de court-circuit donné [6] et des méthodes plus traditionnelles basées sur la détection de fronts d'onde de faille [3,7]. Les méthodes suivantes ont été utilisées pour détecter les fronts d'onde : la transformée en ondelettes, l'analyse en composantes principales basée sur l'extraction de caractéristiques, l'opérateur d'énergie de Teager, la décomposition en mode empirique d'ensemble et la méthode du crayon matriciel, qui est discutée et utilisée dans cet article [8,9]. La méthode du crayon matriciel est utilisée pour décomposer un signal en la somme de sinusoïdes amorties de manière exponentielle [10]. Dans le domaine de l'électrotechnique, la méthode du crayon matriciel a été utilisée pour estimer les modes fondamentaux d'oscillations dus aux défauts et pour estimer les harmoniques et les sous-harmoniques [11,12,13].

Les signaux électriques traités par des algorithmes de traitement de données numériques sont délivrés au relais par l'intermédiaire d'appareils de mesure situés sur la station. Ces dispositifs comprennent des transformateurs de courant et de tension, des bobines de Rogowski ou des capteurs réduisant le niveau des signaux électriques au niveau acceptable par les relais. Il est important que le signal du côté secondaire de ces appareils soit reproduit aussi précisément que possible et, idéalement, il ne devrait être qu'à l'échelle. En pratique, cependant, les instruments de mesure ont un gain et un déphasage variables en fonction de la fréquence du signal. Les hautes fréquences ne doivent pas être trop atténuées par l'instrument afin de pouvoir détecter une onde progressive entrante, qui est une forme d'onde à changement rapide et contient donc des composants haute fréquence. Il faut souligner que pour reproduire avec précision l'amplitude de l'onde de défaut, l'instrument doit introduire un retard constant (de préférence aucun) et ses caractéristiques d'amplification doivent être aussi peu variables que possible.

Les transformateurs sont les instruments traditionnellement utilisés dans l'industrie de l'énergie électrique pour mesurer la tension. Ils se caractérisent par une transformation très précise des signaux électriques, mais ils présentent aussi des inconvénients. Ils contribuent au phénomène négatif de ferrorésonance, sont exposés aux dommages causés par les courts-circuits dans le circuit secondaire et ne sont pas capables de transformer précisément les composantes de tension haute fréquence (>3 kHz) [14]. C'est pourquoi, des capteurs non conventionnels basés sur des mécanismes différents du système de transformateur ont été développés en réponse au besoin de mesurer avec précision les composants transitoires [15,16].

Pour les mesures de tension, les capteurs de tension basés sur des diviseurs capacitifs (C), résistifs (R) et résistifs-capacitifs (RC) sont des capteurs non conventionnels populaires [14]. En particulier, les diviseurs R et RC sont les plus populaires car ils sont incapables d'induire une ferrorésonance en raison d'une inductance négligeable, de transformer les transitoires et les hautes fréquences avec précision, permettant la décharge de la charge accumulée sur la ligne et sont résistants aux courts-circuits du côté secondaire. Ces diviseurs peuvent être utilisés avec succès pour les mesures de la qualité de l'énergie et pour la localisation des courts-circuits à l'aide de phénomènes ondulatoires.

La littérature sur la modélisation des transformateurs conventionnels est vaste mais, malheureusement, se réfère généralement à la description de leurs caractéristiques aux fréquences inférieures à 10 kHz [15,17]. De plus, les auteurs n'ont pas été en mesure de trouver les données numériques des diagrammes de Bode ou des fonctions de transfert des transformateurs de tension (tant conventionnels que non conventionnels) jusqu'à 1 MHz, même dans les articles décrivant les études dans ce domaine [18,19]. De telles données sont disponibles pour un transformateur de courant conventionnel [20]. Bien sûr, les capteurs diffèrent dans leur conception, ce qui entraîne des variations de leurs caractéristiques de transfert d'un type à l'autre mais connaître la fonction de transfert d'un exemple semble nécessaire.

Afin d'obtenir de telles données, des mesures des caractéristiques de fréquence d'un capteur moyenne tension ont été effectuées. Ensuite, ils ont été utilisés pour développer son modèle de fonction de transfert. La méthode améliorée du crayon matriciel court-temps a ensuite été présentée en application à la détection des ondes de court-circuit de tension dans le réseau moyenne tension mesurées au secondaire des capteurs de tension.

La structure du document est la suivante. La section 2 fournit une description de la méthode du crayon matriciel à court terme avec son application pour trouver des impulsions de signal. Il est également prévu l'algorithme d'identification des impulsions. La section 3 contient les résultats de mesure de la fonction de transfert du capteur de tension et les résultats du fonctionnement de l'algorithme sur la base de simulations effectuées. Les conclusions sont données dans la section 4.

2. L'identification des impulsions de défaut dans un réseau moyenne tension

2.1. La méthode du crayon matriciel à court terme

La méthode du crayon matriciel à court terme (STMPM) se rapproche d'un signal à l'intérieur de la fenêtre qui se déplace avec le temps comme la somme de composantes sinusoïdales avec une amplitude exponentiellement variable [10,21] :

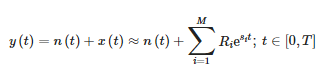
où :

• y(t)—signal de mesure,
• n(t)—bruit,
• x(t)—signal d'origine,
• Ri : amplitudes résiduelles ou complexes des composants,
• Si : pôles complexes et
• M : nombre de composants d'approximation.

Pour un signal échantillonné t = kT_s, l'équation ci-dessus prend la forme suivante :

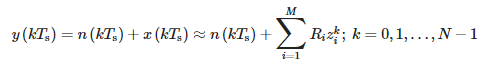
où :

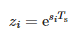
• Ts—période d'échantillonnage et
• N : nombre d'échantillons.

Afin de déterminer les paramètres d'approximation, la matrice suivante doit être construite :

Ici, L est un paramètre crayon. Le nombre de composants d'approximation M satisfait la relation suivante :

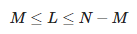
Ainsi, on voit que la valeur maximale de M est égale à ⌊N/2⌋.
En soumettant la matrice Y à une décomposition en valeurs singulières (SVD) on obtient :

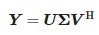
où :

• U—matrice unitaire de taille (N − L) × (N − L),
• Σ—matrice diagonale rectangulaire de valeurs singulières de taille (N − L) × (L + 1) et
• V : matrice unitaire de taille (L + 1) × (L + 1).

Si le signal mesuré ne contenait aucun bruit, la matrice Σ contiendrait exactement M singulier non nul valeurs. En raison du bruit, les valeurs singulières peuvent être déformées, ce qui se manifeste par de petites valeurs singulières supplémentaires. L'effet de bruit est éliminé en supprimant ces petites valeurs. Il ne reste que les valeurs dominantes M qui satisfont la condition suivante :

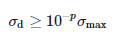
où σ_max est une valeur singulière dominante et p est le nombre de chiffres décimaux significatifs précis de mesure.

Ensuite, des sous-matrices des matrices SVD résultantes sont construites :

1. La matrice U′=[u1,u2,…,u_M] de taille (N − L) × M est créée en laissant les colonnes correspondant aux valeurs singulières satisfaisant la condition (7) et en supprimant les autres ;
2. La matrice diagonale carrée Σ=diag(σ1,σ2,…,σM) est formée en supprimant les colonnes et les lignes de la matrice Σ, qui contiennent des valeurs singulières qui ne satisfont pas la condition (7) ;
3. La matrice V′=[v1,v2,…,v_M] de taille (L + 1) × M est formée en laissant les colonnes correspondant aux valeurs singulières vérifiant la condition (7) et supprimer les autres.

Ensuite, la matrice V₁′ est créée en supprimant la dernière ligne de la matrice V′. V₂′ est construit en supprimant la première ligne de la matrice V′.

Ensuite, les matrices suivantes sont calculées :

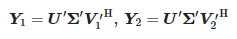
Les valeurs zi sont des valeurs propres généralisées non nulles de la paire de matrices (Y₁, Y₂), à savoir les valeurs propres de Y ^†₁Y₂, où Y^†₁ est la pseudo-inverse de Moore–Penrose de Y₁. Puis on calcule les pôles :

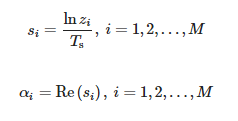
Les valeurs des amplitudes peuvent être déterminées comme suit :

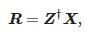
où :

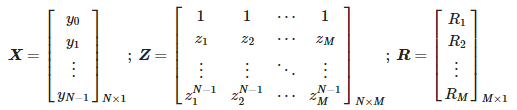
Les opérations ci-dessus sont effectuées dans la méthode du crayon matriciel à court terme pour des intervalles successifs de données [9,22].

Les résultats approximatifs des valeurs propres, des pseudo-inversions et des algorithmes SVD peuvent affecter l'émergence de valeurs zi non nulles mais proches de zéro. Ces valeurs affectent la vitesse MPM et peuvent affecter négativement leurs résultats, il vaut donc la peine de les supprimer avant de calculer les résidus.

2.2. Le comportement des pôles composants au voisinage d'une impulsion

Les défauts du réseau électrique génèrent des impulsions se propageant le long des lignes électriques à des vitesses proches de la vitesse de la lumière [3]. Ces impulsions peuvent être identifiées en utilisant l'analyse de déplacement des pôles de l'approximation STMPM. La figure 1 montre trois exemples d'impulsions de forme gaussienne et les pôles de leur approximation avec STMPM. Lorsque l'impulsion arrive, l'approximation avec des composantes exponentielles change au fur et à mesure que la fenêtre temporelle se déplace. Lorsque l'impulsion est à droite du milieu de la fenêtre, les pôles de l'approximation ont une partie réelle positive, lorsque le sommet gaussien est au milieu de la fenêtre, la partie réelle des pôles est proche de zéro, et lorsque le l'impulsion est dans la première moitié de la fenêtre les pôles ont une partie réelle négative. Le changement de signe de la partie réelle des pôles indique donc que le centre de l'impulsion est passé par le point milieu de la fenêtre d'échantillonnage [9,22]. Nous pouvons également voir sur la figure 2 que les pôles avec la plus grande valeur absolue de la partie réelle (et donc avec le taux de changement d'amplitude le plus rapide) ont la plus grande valeur du module d'amplitude initial (résidu).

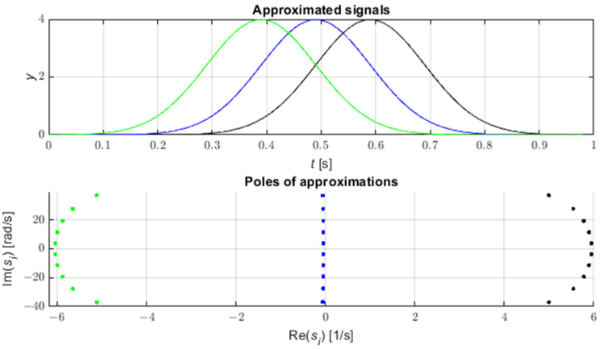
Figure 1. Gaussiennes et pôles d'approximations correspondants.

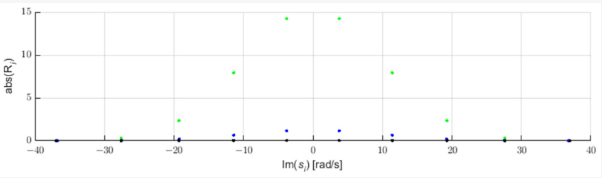
Figure 2. Résidus des composants des approximations gaussiennes.

Ainsi, nous voyons que la coordonnée temporelle du sommet de l'impulsion peut être approximativement identifiée avec le moment de changement du signe des coefficients d'amortissement.

En obtenant l'évolution en fonction du temps de ces coefficients à l'aide de STMPM, nous pouvons les soumettre à une approximation linéaire au voisinage du point où les coefficients passent par zéro et obtenir une coordonnée supérieure approximative de l'impulsion. Il convient de noter que les coefficients caractérisés par la variabilité la plus élevée sont également caractérisés par l'amplitude la plus élevée - ce sont les plus grandes composantes de l'impulsion.

2.3. L'algorithme de détection d'impulsions en temps réel

L'organigramme de l'algorithme de détection des impulsions provenant des ondes progressives est présenté à la figure 3. L'algorithme soumet des fenêtres successives du signal à STMPM afin d'extraire les taux de décroissance des composantes d'approximation.

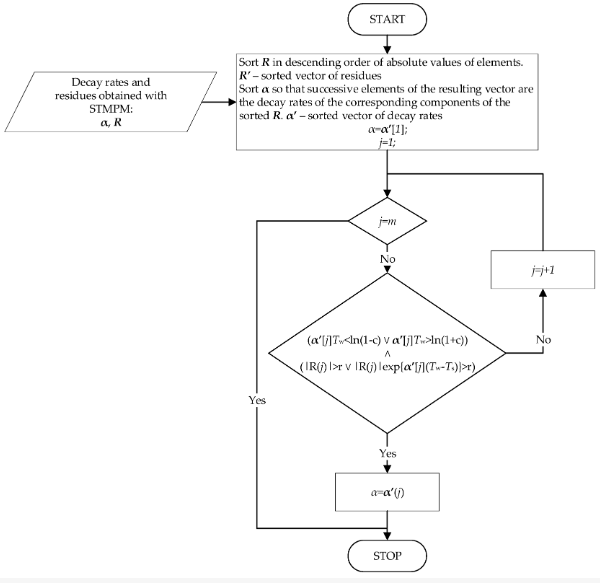
Figure 3. L'algorithme de sélection des taux de décroissance.

Les composants obtenus sont soumis à une sélection, dont la procédure est présentée à la figure 4. La sélection est basée sur l'hypothèse que les composants du STMPM, qui sont caractérisés par la plus grande amplitude, doivent être pris pour le temps de pointe approximation - ils constituent la plus grande contribution à la composante transitoire du signal. Ceci est en accord avec l'observation du point précédent - les composants avec la plus grande variation d'amplitude sont caractérisés par la plus grande amplitude initiale. Dans le cas où la composante avec la plus grande amplitude est caractérisée par un faible taux de décroissance pendant toute la fenêtre de longueur T_w - inférieure au paramètre c - ou sa contribution maximale au signal est inférieure à r, la composante suivante en termes d'amplitude d'amplitude est sélectionnée comme candidat potentiel pour le taux de décroissance α. En répétant cette procédure pour les composantes suivantes jusqu'à ce que la condition soit remplie, on obtient finalement le coefficient α qui sert alors à approximer l'instant d'arrivée de l'impulsion. Si aucune des composantes ne satisfait aux conditions ci-dessus, celle dont l'amplitude est la plus élevée est sélectionnée.

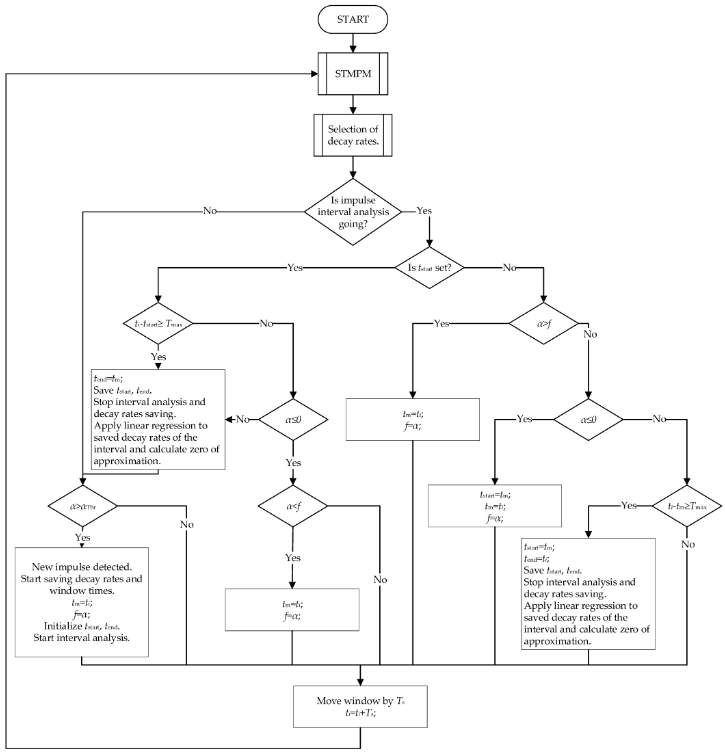
Figure 4. L'algorithme d'identification des impulsions.

Le temps associé à une fenêtre est considéré comme :

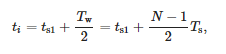
où t_s1—heure du premier échantillon de fenêtre et T_w—largeur de fenêtre.

L'arrivée d'une impulsion est indiquée par une forte augmentation des taux α associée à un changement rapide du signal à la fin de la fenêtre d'échantillonnage. Le paramètre α_Thr est sélectionné comme seuil des taux de décroissance. Lorsque le seuil de détection est dépassé, les valeurs suivantes des coefficients α et des temps de fenêtre sont écrites dans la mémoire, et l'analyse des données est lancée pour déterminer des limites d'impulsion plus précises. Le moment t_start avec la valeur la plus élevée de α avant de changer le signe du taux de décroissance est sélectionné comme le bon début de l'impulsion. Afin de stocker les temps potentiels des limites d'impulsion correctes, la variable t_m a été introduite avec la variable f contenant les plus grandes valeurs de α de l'impulsion calculées jusqu'à présent.

Si la valeur de t_start est trouvée, la recherche de la fin propre de l'impulsion t_end démarre. Cela correspond à la plus petite valeur de α avant que le signe ne change à nouveau, cette fois vers le positif. La variable i_m est à nouveau utilisée pour stocker les points de terminaison potentiels précédents. La variable f contient les valeurs α minimales précédentes.

Lorsque la longueur de l'impulsion est égale à la T_max des échantillons ou que la fin de l'impulsion est trouvée, l'analyse de l'impulsion est terminée.

Fonction α(t) dans l'intervalle [t_start ; t_end] est soumis à une régression linéaire. Les coefficients de cette régression sont trouvés comme solution au problème suivant :

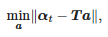
où : α_t=[α(t_début),α(t_début+Ts),…,α(t_end)]^T, a=[a₁,a₀]^T

Les coefficients recherchés sont :

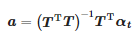
Alors que le moment d'arrivée de l'impulsion est :

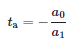
2.4. Le chargeur de test IEEE 34-Bus adapté

Pour les calculs de court-circuit, un modèle de chargeur de test IEEE à 34 bus dans Simulink a été créé. La topologie du feeder est illustrée à la Figure 5 [23]. Le chargeur est basé sur un réseau réel dans l'état de l'Arizona. C'est assez simple pour ne pas devenir une charge de calcul substantielle lors de simulations transitoires avec un petit pas d'intégration. Le modèle a été simplifié et les paramètres modifiés pour imiter les grilles européennes :

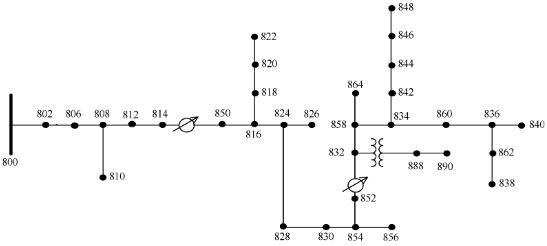
Figure 5. La topologie du chargeur de bus IEEE 34.

• La tension du réseau est passée de 24,9 kV à 16,5 kV ;
• Tous les tronçons de lignes électriques ont été supposés être des lignes aériennes avec les mêmes paramètres ;
• Les régulateurs de tension ont été supprimés ;
• Les charges réparties étaient supposées être regroupées dans les bus à l'extrémité des lignes chargées ;
• Les charges étaient connectées au réseau moyenne tension via des transformateurs de distribution ;
• Le point neutre du transformateur haute/moyenne tension a été déconnecté de la terre.

Paramètres de la source de tension :

• Fréquence 50 Hz ;
• Tension de ligne de 115,5 kV ;
• Résistance 0,00227 Ω.
• Source symétrique avec déphasage de la phase L1 égal à 0°.

Paramètres du transformateur de puissance :

• Rapport de tension 115,5/16,5 ;
• Groupe vectoriel d'enroulement haute tension Yg ;
• Groupe vectoriel de l'enroulement basse tension D11 ;
• Puissance 6,3 MVA ;
• Tension de court-circuit relative 7,5 % ;
• Résistance aux courts-circuits égale à 0,49 % de l'impédance équivalente.

Paramètres des transformateurs de distribution :

• Rapport de tension 15,75/0,4 ;
• Groupe vectoriel de l'enroulement haute tension D11 ;
• Groupe vectoriel d'enroulement basse tension Yg ;
• Puissance 630 kVA ;
• Tension de court-circuit relative 6 % ;
• Résistance aux courts-circuits égale à 17,2 % de l'impédance équivalente.

Paramètres des lignes électriques :

• Ligne triphasée sans neutre ;
• Un conducteur par phase ;
• Diamètre du conducteur 0,8466 cm ;
• Rapport T/D 0,311 ;
• Résistance CC 0,5939 Ω/km ;
• Positions horizontales des conducteurs x=[−1.05, 0, 1.05] ;
• Positions verticales des conducteurs u=[−9.05, 10.61, 9.05] ;
• Résistivité du sol ρ=100 Ωm.

Des capacités ont été fixées à chaque transformateur, comme illustré à la figure 6 [5] dans afin de modéliser les propriétés des transformateurs aux hautes fréquences.

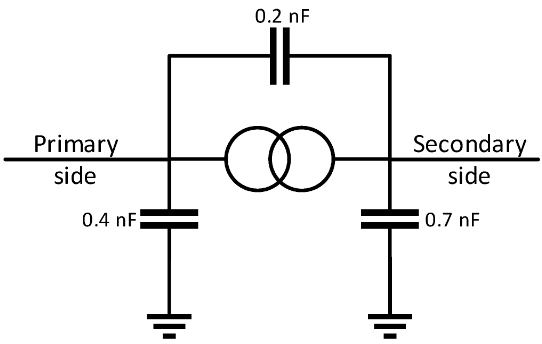
Figure 6. Modèle de transformateur.

Les lignes électriques ont été modélisées entre 1 Hz et 1 MHz en tenant compte de l'effet de peau à l'aide du modèle de ligne universel.

Des simulations de courts-circuits monophasés et multiphasés avec résistance au passage par zéro ont été réalisées à 20 %, 50 %, 80 % et 100 % de longueur de lignes. Il correspond à 76 emplacements de court-circuit. Le pas d'intégration de la simulation était Δt=0.1 μs. Tustin/Backward Euler était la méthode d'intégration utilisée.

3. Résultats

3.1. Mesures des caractéristiques de transmission du capteur moyenne tension

Les mesures de la réponse en fréquence ont été réalisées pour un capteur moyenne tension destiné à être monté dans des têtes de connecteurs. Le capteur était un diviseur résistif avec une tension primaire nominale de 20/√3 kV et une tension secondaire nominale de 3,25/√3, ce qui correspond au rapport de tension :

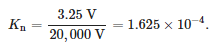
L'analyseur de réseau vectoriel Bode 100 d'OMICRON Lab a été utilisé pour les mesures. Cet appareil permet les mesures dans la plage de 1 Hz à 50 MHz. La fonction de mesure de gain et de phase de l'appareil a été utilisée pour effectuer les tests. Cette fonction était basée sur la comparaison de l'amplitude et de la phase des signaux de tension sur les côtés primaire et secondaire du capteur. La mesure de la fonction de transfert, définie comme le rapport de la tension du côté secondaire à la tension du côté primaire, a été effectuée pour 2048 valeurs de fréquence dans la plage de 10 Hz à 20 MHz. Les valeurs mesurées sont présentées dans la figure 7.

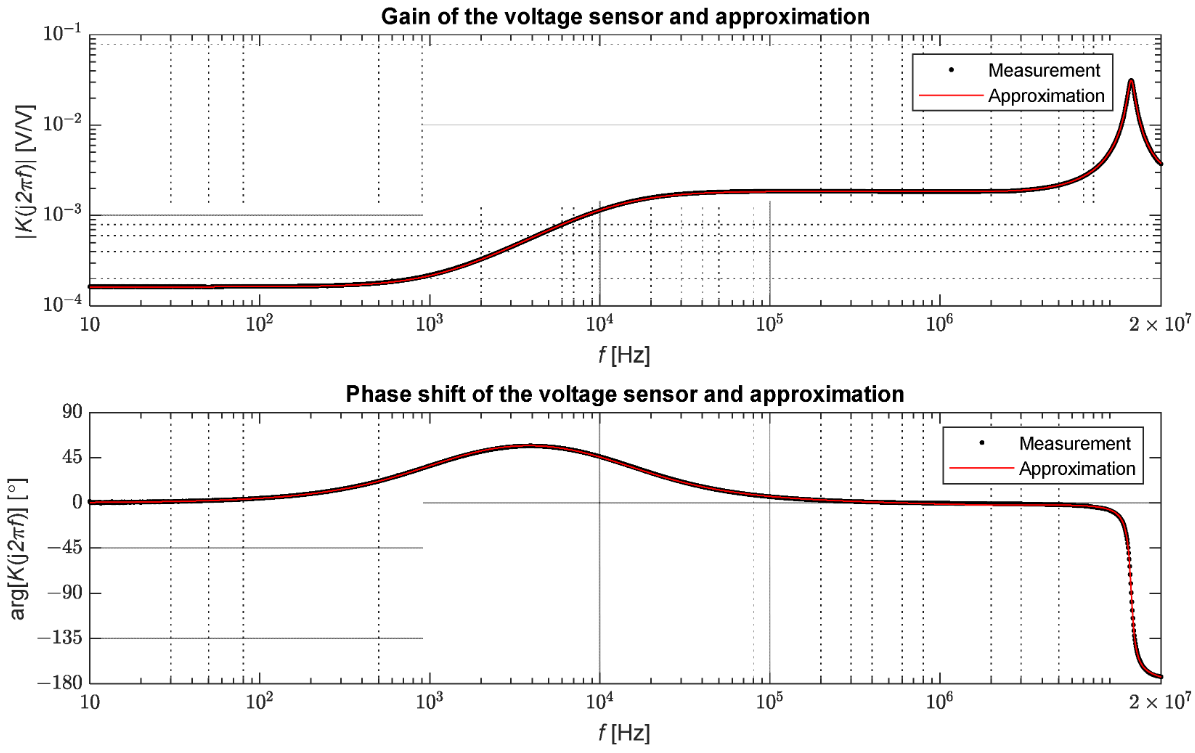
Figure 7. Résultats de mesure de la transmission du capteur moyenne tension.

Le capteur de tension testé maintient un coefficient de transfert nominal pour les signaux jusqu'à la fréquence d'environ 1 kHz, puis le tracé monte au niveau de gain d'environ 1,84 ×10⁻³ ; ce niveau est maintenu entre environ 12,5 kHz et 6,6 MHz. Du fait de la propriété différenciatrice du capteur, on observe un déphasage positif d'environ 57° dans la zone de transition de 100 Hz à 100 kHz. Dans le cas de la phase, on peut distinguer deux zones pour lesquelles le décalage ne dépasse pas 6°. Dans ce cas, la gamme de fréquences va jusqu'à environ 130 Hz et de 105 kHz à 9,4 MHz. Par conséquent, on peut conclure que dans la plage de 105 kHz à 6,6 MHz, les signaux sont transformés proportionnellement mais avec un facteur de proportionnalité différent de celui à proximité de la fréquence du réseau. Dans le cas de phénomènes ondulatoires, cette plage est suffisante pour représenter avec précision la forme des ondes se propageant dans une grille [20]. Il convient de noter que les capteurs de tension de constructions différentes peuvent présenter des propriétés de transfert différentes.

Afin de développer un modèle mathématique du capteur, la fonction "tfest" de MATLAB a été utilisée pour approximer les données obtenues par une fonction de transfert stable de la forme suivante :

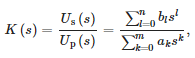
où :

• Up(s) : tension sur le côté primaire du capteur,
• Us(s) — tension sur le côté secondaire du capteur,
• n — l'ordre du numérateur,
• m — l'ordre du dénominateur et
• ak, bl —coefficients des polynômes du dénominateur et du numérateur de la transmission, successivement.

Les valeurs des coefficients de la fonction de transfert sont présentées dans le tableau 1. Il convient de noter que la transmittance modélisée est appropriée car l'ordre du dénominateur est supérieur à l'ordre du numérateur. La figure 7 présente également la comparaison des fonctions de transfert obtenues à partir des mesures avec l'approximation par la formule (19). L'erreur quadratique moyenne entre les points de mesure et l'approximation déterminée par la relation suivante a également été calculée :

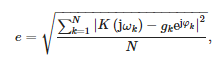
où :

• N = 2 048 : nombre de fréquences de mesure
• g_k — gain mesuré du capteur à la pulsation ω_k et
• φ_k : déphasage mesuré du capteur à la pulsation ω_k.

La valeur d'erreur d'approximation est égale à :

Tableau 1. Valeurs des coefficients polynomiaux de la transmission équivalente d'un capteur de tension à structure de diviseur résistif.

La figure 8 montre la comparaison de la forme d'onde de la tension de phase au poste obtenue à partir de la simulation et de la tension à la sortie du capteur modélisé dans le cas d'un court-circuit triphasé direct avec la terre au nœud 816. Il est clairement visible que l'amplification des transitoires rapides est supérieure à celle des transitoires lents. Il convient de noter que ces formes d'onde sont amplifiées presque proportionnellement.

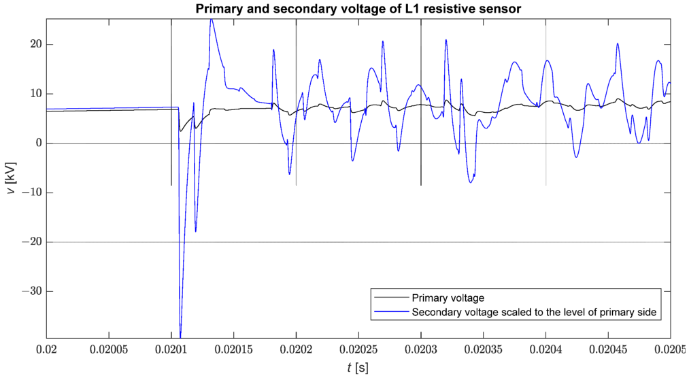
Figure 8. Comparaison de la forme d'onde de la tension de phase (v_L1) et de la tension à la sortie du capteur mise à l'échelle de la tension primaire (v_L1/K_n) pendant le défaut.

3.2. L'identification des impulsions de court-circuit à l'aide de STMPM

La figure 9 montre la forme d'onde de tous les taux de décroissance d'un exemple de forme d'onde de tension dans une sous-station après un court-circuit triphasé à impédance nulle à la terre au nœud 816 du modèle. On peut voir que le manque de sélection des taux de décroissance rend les impulsions difficiles à localiser ; ceci est particulièrement vrai pour les impulsions plus faibles. D'autre part, l'observation visuelle des taux de décroissance permet d'identifier facilement les intervalles contenant des impulsions dans le cas de l'analyse visuelle des formes d'onde de tension de phase, bien que ce ne soit pas toujours facile dans le cas de petites amplitudes d'impulsion.

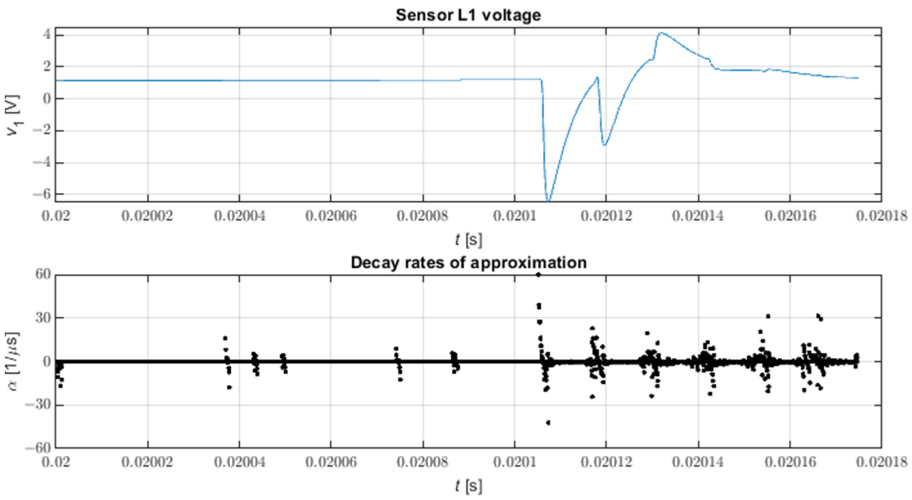
Figure 9. Tous les taux de décroissance de l'approximation STMPM. N = 9, L = 4.

La figure 10 montre les taux de décroissance sélectionnés ainsi que la régression linéaire utilisée pour identifier le moment d'arrivée de l'impulsion. Le nombre de fausses détections d'impulsions peut être réduit en filtrant les coefficients d'atténuation inutiles.

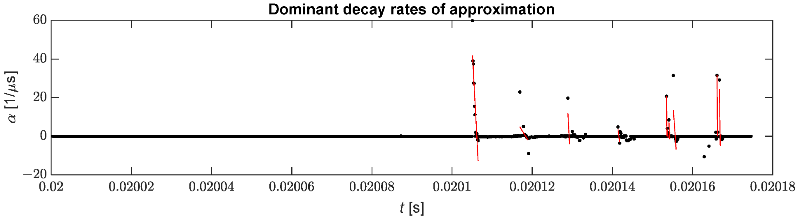
Figure 10. Taux de décroissance sélectionnés utilisés pour l'identification des impulsions.

Le tableau 2 montre les erreurs d'identification de l'heure d'arrivée de la première vague entrante à la station. Cette erreur est définie par l'équation suivante :

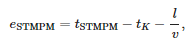
où :

• t_STMPM — moment d'arrivée selon STMPM,
• t_K — moment de défaut,
• l —distance de l'emplacement du court-circuit à la sous-station et
• v = 299 552 300 m/s : vitesse de propagation des ondes de défaut mesurée pour un court-circuit au nœud le plus éloigné (838).

Les paramètres de méthode utilisés pour obtenir les résultats sont :

• N = 5 : nombre d'échantillons par fenêtre temporelle ;
• L = 2—paramètre crayon ;
• p = 6 : le nombre de chiffres décimaux significatifs précis de la mesure ;
• α_Thr=1051s — seuil de détection d'impulsion ;
• T_max=2,1 μs — largeur d'impulsion maximale ;
• T_w=0,5 μs : largeur de la fenêtre ;
• T_s=0,1 μs — période d'échantillonnage ;
• r=0,02 V —seuil d'amplitude.

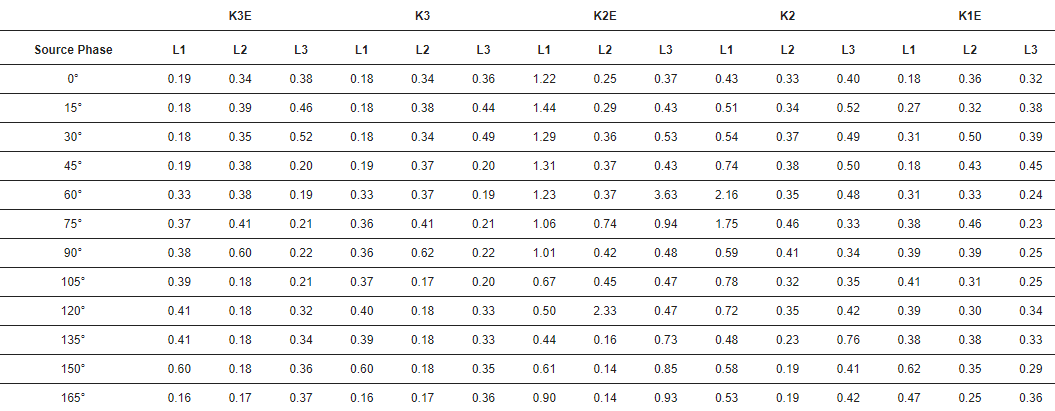
Le tableau 3 montre les écarts-types de l'erreur temporelle de l'impulsion.

Tableau 2. Erreur temporelle d'identification des ondes en cas de défauts différents. Unité : µs. K3E—défaut triphasé-terre, K3—défaut triphasé, K2E—défaut biphasé-terre, K2—défaut biphasé, K1E—défaut phase-terre.

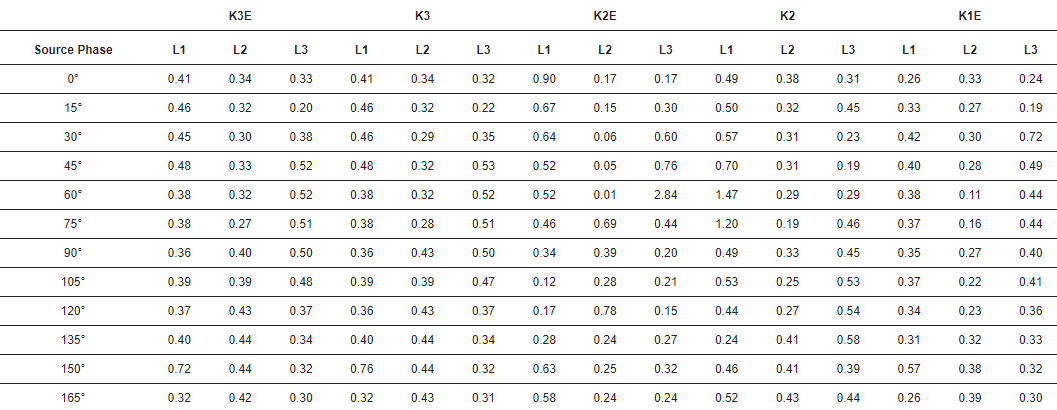
Tableau 3. Écart type de l'erreur temporelle. Unité : µs. K3E—défaut triphasé-terre, K3—défaut triphasé, K2E—défaut biphasé-terre, K2—défaut biphasé, K1E—défaut phase-terre.

4. Débat

Le modèle de fonction de transfert d'un capteur de tension résistif basé sur les mesures à large bande de 10 Hz à 20 MHz a été développé. Les simulations d'ondes progressives générées par défaut dans le modèle IEEE 34-bus ont été réalisées à l'aide de la fonction de transfert. La réponse en fréquence du capteur résistif était suffisante pour l'identification des ondes de défaut dans le signal de tension secondaire. Le capteur transforme les signaux d'ondes progressives avec un gain approximativement constant, qui est supérieur au gain à la fréquence de service. Un nouvel algorithme en temps réel basé sur la méthode du crayon matriciel a été utilisé pour l'identification. La variation de cette méthode utilisée dans l'article est caractérisée par la haute précision de l'identification des ondes, car l'erreur moyenne était de 0,41 µs à un échantillonnage de 10 MHz, et l'erreur avait une valeur positive de sorte que le temps d'arrivée trouvé était plus grand que le vrai. Cependant, il convient de noter que dans les applications pratiques de la méthode, par exemple dans la localisation de défauts par ondes, la partie de cette erreur est éliminée en raison du fonctionnement différentiel de ces algorithmes. L'identification précise des ondes de défaut peut permettre de classer et de localiser les défauts dans les réseaux moyenne tension en utilisant le jeu de barres comme seul point de mesure. Un test utilisant des signaux réels est nécessaire pour vérifier l'efficacité de l'algorithme et le comparer avec d'autres méthodes d'identification des impulsions d'ondes entrantes. Une transformation de tension tout à fait correcte par des capteurs peut permettre la classification du type de défaut en fonction des amplitudes des ondes générées par ceux-ci.

Références

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Article de: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).