Identyfikacja fal wędrujących w sygnale sensora napięciowego w sieci średniego napięcia

W badaniach został zastosowany wektorowy analizator obwodów Omicron-Lab Bode 100 udostępniony przez DACPOL SP. Z O.O.

Streszczenie

Większość metod falowej lokalizacji miejsc zwarcia opiera swe działanie na analizie prądu linii przekształconego przez przekładniki prądowe i ograniczona jest do sieci WN. W artykule przedstawiono wyniki modelowania matematycznego napięciowego sensora SN w szerokim zakresie częstotliwości – od 1 Hz do 20 MHz. Następnie wykorzystano ten model do testów nowego algorytmu czasu rzeczywistego identyfikacji fal zwarciowych opartego na metodzie pęku macierzy. Opracowany algorytm może zostać wykorzystany do lokalizacji falowej miejsc zwarcia.

1. Wprowadzenie

Jednym z celów automatyki zabezpieczeniowej jest ochrona systemu elektroenergetycznego przed zakłóceniami. Szybkie usunięcie zakłócenia ogranicza uszkodzenia zadane urządzeniom elektroenergetycznym, jak i zmniejsza jego negatywny wpływ na jakość energii elektrycznej. Opracowanie szybkich i dokładnych zabezpieczeń oraz lokalizatorów miejsc zwarcia w sieciach dystrybucyjnych jest więc zagadnieniem kluczowym zarówno z technicznego, jak i ekonomicznego punktu widzenia. Sieci dystrybucyjne cechują się strukturą drzewiastą, pomiary są w nich wykonywane głównie w jednym punkcie – w podstacji. Utrudnia to możliwości dokładnej i szybkiej lokalizacji miejsc zwarcia – w sieciach WN, cechujących się dużym rozproszeniem pomiarów i strukturą pętlową nie stanowi to problemu. Rozwiązaniem problemu może być zastosowanie falowych lokalizatorów miejsc zwarcia, które mogą być w tym przypadku precyzyjniejsze niż metody konwencjonalne. By umożliwić ich stosowanie należy opracować jak najdokładniejsze metody identyfikacji fal wędrownych.

Konwencjonalne podejście do wykrywania zakłóceń opiera się na analizie prądów i napięć o częstotliwości podstawowej. Z tego względu algorytmy zabezpieczeniowe oparte na tego typu sygnałach wymagają analizy na tyle długiego odcinka sygnału, by upewnić się, co do wystąpienia zakłócenia . Nowocześniejsze podejście oparte jest na sygnałach o wyższej częstotliwości propagujących się wzdłuż linii energetycznych – falach wędrujących. Tego typu zabezpieczenia czasami nazywane są „ultra-szybkimi”. Wykrywają one fale prądów i napięć generowane przez zakłócenia, by następnie na podstawie porównania ich amplitud oraz czasów przybycia do aparatów pomiarowych określić zarówno rodzaj, jak i lokalizację zakłócenia. Niewątpliwą zaletą zabezpieczeń falowych jest oczywiście szybkość działania (mniejsza od 4 ms) [1]. Ponadto działają one poprawnie w przypadku kompensowanych szeregowo linii przesyłowych oraz podczas kołysań mocy.

Zabezpieczenia falowe można podzielić na dwukrańcowe i jednokrańcowe. W przypadku przekaźników dwukrańcowych akwizycja danych pomiarowych występuje na krańcach zabezpieczanych linii – wymaga to przesyłania informacji pomiarowych między urządzeniami. Przekaźniki jednokrańcowe analizują sygnały prądów i napięć z tylko jednego punktu pomiarowego. Zabezpieczenia dwukrańcowe charakteryzują się większą niezawodnością, gdyż do lokalizacji i klasyfikacji zakłócenia wykorzystują fale bezpośrednio wygenerowane przez zakłócenie. Fale te cechują się największą możliwą amplitudą i są wykrywane jako pierwsze po zwarciu. W przypadku zabezpieczeń jednokrańcowych, ze względu na brak drugiego punktu pomiarowego w sieci, zabezpieczenie musi opierać swe działania na fali wygenerowanej przez zakłócenie oraz na falach odbitych od nieciągłości linii, rozgałęzień oraz samego zwarcia.

Zabezpieczenia dwukrańcowe wykorzystywane są w sieciach przesyłowych wysokiego napięcia ze względu na występowanie na krańcach linii podstacji elektroenergetycznych z aparatami pomiarowymi. W przypadku sieci dystrybucyjnych zwykle jedynym punktem w którym umieszczane są przekaźniki zabezpieczeniowe wraz z przekładnikami bądź sensorami są podstacje SN/nN. Oznacza to, że w sieciach dystrybucyjnych najtańszym rozwiązaniem jest stosowanie falowych zabezpieczeń jednokrańcowych.

Sieci dystrybucyjne cechują się dodatkową właściwością, które utrudnia poprawną lokalizację zwarć – są sieciami o topologii drzewiastej. Zarówno dla konwencjonalnych, jak i falowych lokalizatorów miejsc zwarcia sytuacja jest tu bardziej skomplikowana niż w sieciach przesyłowych, gdyż może istnieć kilka potencjalnych miejsc zwarcia przy znanej jego odległości od stacji. Zwartą linię można jednakże określić na podstawie porównania amplitud fal prądowych rozproszonych na szynach stacji [2,3,4].

Do lokalizacji miejsc zwarcia zaproponowano metody oparte na wykrywaniu częstotliwości powiązanych z oscylacjami fal pomiędzy węzłami [5], porównaniu zmierzonego sygnału prądowego z przewidywanym dla danego miejsca zwarcia [6] jak i bardziej tradycyjne metody oparte na wykrywaniu czół fal zakłóceniowych [3,7]. Do wykrywania czół fali wykorzystywano: transformatę falkową, analizę głównych składowych, operator energetyczny Teagera, Ensemble empirical mode decomposition oraz omawianę w niniejszym artykule metodę pęku macierzy [8,9]. Metoda pęku macierzy wykorzystywana jest do rozłożenia sygnału na sumę tłumionych wykładniczo sinusoid [10]. Sama metoda pęku macierzy w dziedzinie elektroenergetyki wykorzystywana była do szacowania modów podstawowych drgań powstałych na skutek zakłóceń, szacowania harmonicznych i subharmonicznych [11,12,13].

Sygnały elektryczne poddawane obróbce przez cyfrowe algorytmy przetwarzania dostarczane są do przekaźnika za pomocą mieszczących się na stacji aparatów pomiarowych – przekładników prądowych, napięciowych, cewek Rogowskiego, bądź sensorów zmniejszających wartość sygnałów elektrycznych do poziomu dopuszczalnego przez przekaźniki. Ważne jest, by sygnał po stronie wtórnej wspomnianych aparatów był jak najwierniej odwzorowywany – w sytuacji idealnej powinien być on po prostu przeskalowany. W praktyce jednak aparaty pomiarowe charakteryzują się zmiennymi właściwościami w zależności od częstotliwości sygnału – różnym wzmocnieniem i różnym przesunięciem fazowym. By możliwe było wykrycie nadchodzącej fali zakłóceniowej będącej przebiegiem szybkozmiennym, a więc zawierającym składowe wysokoczęstotliwościowe częstotliwości te nie powinny być nazbyt tłumione przez aparat. By wiernie odwzorować amplitudę fali zwarciowej charakterystyka wzmocnienia aparatu dla częstotliwości tworzących falę powinna być jak najmniej zmienna i wprowadzać stałe opóźnienie czasowe (a najlepiej żadnego).

Tradycyjnie wykorzystywanymi w elektroenergetyce aparatami do pomiaru napięcia są przekładniki. Cechują się one bardzo wierną transformacją tej wielkości elektrycznej, lecz posiadają również wady. Przyczyniają się do negatywnego zjawiska ferrorezonansu, są narażone na uszkodzenia wywołane zwarciami w obwodzie wtórnym, nie są w stanie wierne odwzorowywać składowych napięcia o wysokich częstotliwościach (>3 kHz) [14]. W odpowiedzi na potrzeby związane z dokładnym pomiarem składowych przejściowych opracowano przekładniki niekonwencjonalne opierające się na innych mechanizmach niż układ transformatora [15,16].

W przypadku pomiarów napięć popularnymi przekładnikami niekonwencjonalnymi są sensory napięciowe oparte na dzielnikach: pojemnościowych (C), rezystancyjnych (R) oraz rezystancyjno-pojemnościowych (RC) [14]. W szczególności dwa ostatnie mogą pochwalić się większą użytecznością niż przekładniki konwencjonalne. Dzielniki R i RC nie są w stanie wywołać ferrorezonansu ze względu na pomijalną indukcyjność, wiernie odwzorowują składowe przejściowe i wysokie częstotliwości, umożliwiają rozładowanie zgromadzonego na linii ładunku oraz są odporne na zwarcia strony wtórnej. Dzielniki te mogą z powodzeniem być wykorzystywane do pomiarów jakości energii elektrycznej oraz do lokalizacji zwarć z wykorzystaniem zjawisk falowych.

Literatura dotycząca modelowania konwencjonalnych przekładników jest bogata, lecz, niestety, zwykle odnosi się do opisu ich właściwości w częstotliwościach poniżej 10 kHz [15,17]. Co więcej, autorom nie udało się odnaleźć danych liczbowych charakterystyk przenoszenia lub transmitancji przekładników napięciowych (zarówno konwencjonalnych, jak i niekonwencjonalnych) do 1 MHz, nawet w artykułach opisujących badania w takim spektrum [18,19]. W przypadku tradycyjnego przekładnika prądowego takie dane są dostępne [20].

W celu uzyskania takich danych wykonano pomiary charakterystyk częstotliwościowych sensora SN, które następnie wykorzystano do opracowania jego modelu transmitancji. Następnie przedstawiono usprawnioną metodę pęku macierzy w zastosowaniu do wykrywania napięciowych fal zwarciowych w sieci SN po stronie wtórnej sensorów napięciowych.

2. Identyfikacja impulsów zwarciowych w sieci SN

2.1. Krótkoczasowa metoda pęku macierzy

Krótkoczasowa metoda pęku macierzy (KMPM) opiera się na aproksymacji sygnału wewnątrz przesuwającego się wraz z czasem okna na sumę składowych sinusoidalnych o zmiennej wykładniczo amplitudzie [10,21]:

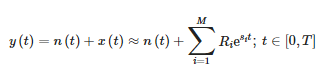
gdzie:

• y(t) — sygnał pomiarowy,
• n(t) — szum,
• x(t) — właściwy sygnał,
• Ri — rezidua lub amplitudy zespolone składowych,
• Si — bieguny zespolone
• M — liczba składowych aproksymacji.

W przypadku sygnału spróbkowanego t = kT_s a powyższe równanie otrzymuje następującą postać:

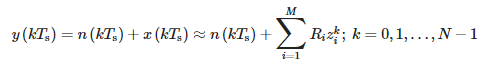
gdzie:

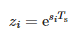
• Ts — okres próbkowania i
• N — liczba próbek.

W celu wyznaczenia parametrów aproksymacji konstruuje się następującą macierz:

L oznacza tutaj parametr pęku macierzy. Liczba składowych aproksymacji M spełnia następującą zależność:

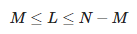
Widzimy więc, że maksymalna wartość M jest równa ⌊N/2⌋.
Poddając macierzy Y rozkładowi według wartości osobliwych otrzymujemy:

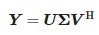
gdzie:

• U — unitarna macierz o rozmiarze (N − L) × (N − L),
• Σ — macierz diagonalna wartości osobliwych o rozmiarze (N − L) × (L + 1) i
• V — unitarna macierz o rozmiarze (L + 1) × (L + 1).

W przypadku, gdy zmierzony sygnał nie zawierałby szumu, macierz Σ mieściłaby dokładnie M niezerowych wartości osobliwych. Ze względu na szum może nastąpić zaburzenie wartości osobliwych objawiające się pojawieniem dodatkowych niewielkich wartości. Eliminacja wpływu szumu wykonywana jest tu poprzez usunięcie tych niewielkich wartości – pozostawia się tylko M, dominujących, które spełniają następujący warunek:

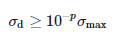
gdzie σ_max to największa wartość osobliwa, a p liczba cyfr znaczących rozwinięcia dziesiętnego danych pomiarowych.

Konstruuje się następnie podmacierze macierzy wynikowych rozkładu SVD:

1. macierz U′=[u₁,u₂,…,u_M] rozmiaru (N − L) × M powstałą przez pozostawienie kolumn odpowiadających wartościom osobliwym spełniającym warunek (x) i usunięcie pozostałych,
2. kwadratową macierz diagonalną Σ = diag(σ₁,σ₂,…,σ_M) powstałą przez usunięcie kolumn i rzędów macierzy na których leżą wartości osobliwe niespełniające warunku (x),
3. macierz V′=[v₁,v₂,…,v_M] rozmiaru (L + 1) × M powstałą przez pozostawienie kolumn odpowiadających wartościom osobliwym spełniającym warunek (x) i usunięcie pozostałych.

Dalej tworzy się macierz V₁′ przez usunięcie ostatniego rzędu macierzy V′ oraz macierz V₂′ przez usunięcie pierwszego rzędu macierzy V′.

Oblicza się następnie macierze:

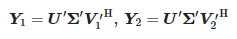
Wartości z_i wyznacza się jako niezerowe uogólnione wartości własne pary macierzy (Y₁, Y₂), czyli wartości własne macierzy Y ^†₁Y₂, gdzie Y^†₁ to pseudoodwrotność Moore’a-Penrose’a macierzy Y₁. Mamy więc:

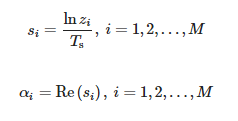
Wartości amplitud można wyznaczyć w następujący sposób:

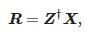
gdzie:

Powyższe operacje wykonuje się w krótkoczasowej metodzie pęku macierzy dla kolejnych przedziałów analizy danych [9,22].

Przy numerycznej implementacji algorytmu KMPM należy zwrócić uwagę na to, że błędy przybliżenia maszynowego oraz przybliżona natura wyników algorytmów obliczających wartości własne, osobliwe oraz pseudoinwersje może skutkować pojawieniem się niezerowych, choć bliskich zeru wartości z_i. Wartości te wpływają na szybkość MPM i mogą negatywnie wpływać na ich wyniki, więc warto je usunąć przed obliczaniem residuów.

2.2. Zachowanie biegunów składowych w pobliżu impulsu

Zwarcia w sieci generują impulsy propagujące się wzdłuż linii elektroenergetycznych z prędkością bliską prędkości światła [3]. Impulsy te da się zidentyfikować z wykorzystaniem analizy zmian biegunów aproksymacji KMPK. Figura 1 przedstawia trzy przykładowe impulsy o kształcie Gausjanu oraz bieguny ich aproksymacji z pomocą KMPK. W przypadku wystąpienia impulsu wraz z przesuwaniem się okna czasowego zmienia się aproksymacja składowymi wykładniczymi. Gdy impuls jest na prawo od środkowego punktu okna bieguny aproksymacji mają rzeczywistą część dodatnią, gdy wierzchołek Gausjanu mieści się w środkowym punkcie okna część rzeczywista biegunów jest bliska zeru, gdy impuls mieści się w pierwszej połowie okna bieguny mają ujemną część rzeczywistą. Zmiana znaku części rzeczywistej biegunów świadczy więc o przejściu środka impulsu przez środkowy punkt okna próbkowania [9,22]. Z Figury 2 widzimy również, że bieguny o największej wartości bezwzględnej części rzeczywistej (a więc o najszybszej zmienności amplitudy) charakteryzują się największą wartością modułu amplitudy początkowej (residuum).

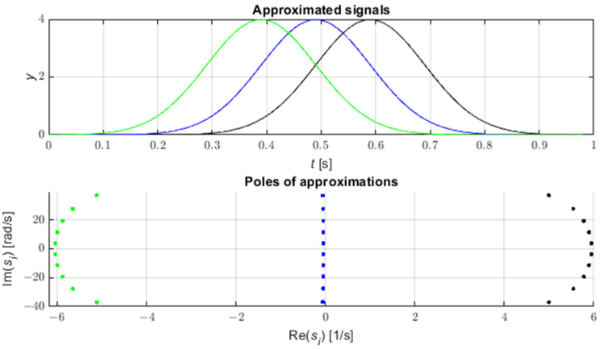
Figure 1. Gaussians and corresponding poles of approximations.

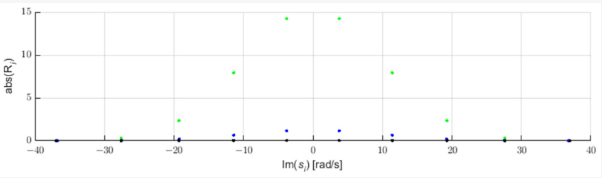
Figure 2. Residues of components of Gaussian approximations.

Widzimy więc, że współrzędną czasową wierzchołka impulsu możemy w przybliżeniu utożsamić z chwilą zmiany znaku współczynników tłumienia.

Uzyskując przebieg tychże współczynników w zależności od czasu z wykorzystaniem KMPM możemy poddać je aproksymacji liniowej w sąsiedztwie miejsca przejścia współczynników przez zero i uzyskać przybliżoną współrzędną wierzchołka impulsu. Należy zwrócić uwagę, że współczynniki cechujące się największą zmiennością charakteryzują się również największą amplitudą – są największymi składowymi impulsu.

2.3. Algorytm wykrywania impulsów w czasie rzeczywistym

Schemat blokowy algorytmu umożliwiającego wykrywanie impulsów pochodzących od fal wędrujących przedstawia Figura 3. Algorytm poddaje kolejne okna sygnału KMPM w celu ekstrakcji współczynników tłumienia składowych aproksymacji.

Uzyskane składowe podlegają selekcji, której procedura przedstawiona jest na Figurze 4. Selekcja ta opiera się na założeniu, że do aproksymacji czasu wierzchołka powinny być brane te składowe aproksymacji KMPM, które charakteryzują się największą amplitudą – to one stanowią największy wkład w składową przejściową sygnału. Stoi to w zgodzie ze spostrzeżeniem z poprzedniego punktu – największą amplitudą początkową cechują się składowe o największej zmienności amplitudy. W przypadku, gdy składowa o największej amplitudzie cechuje się niewielką zmiennością – mniejszą niż parametr c w ciągu całego okna o długości T_w lub jej maksymalny wkład w sygnał jest mniejszy niż r, jako potencjalnego kandydata na współczynnik tłumienia α dobiera się kolejną składową pod względem amplitudy. Powtarzając tę procedurę wobec kolejnych składowych, aż do spełnienia warunku, uzyskuje się ostatecznie współczynnik α wykorzystywany dalej do aproksymacji czasu przybycia impulsu. W przypadku, gdy żadna ze składowych nie spełnia powyższych warunków dobierana jest ta o najwyższej amplitudzie.

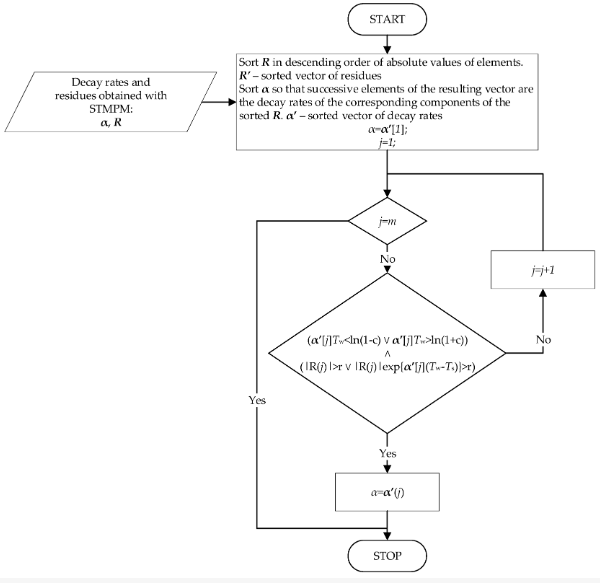
Figure 3. Algorithm of selection of decay rates.

Za czas stowarzyszony z danym oknem uznaje się:

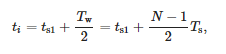
gdzie t_s1—czas pierwszej próbki okna, T_w—szerokość okna.

O przybyciu impulsu informuje gwałtowny wzrost współczynników α związany z szybką zmianą sygnału na końcu okna próbkowania. Jako próg współczynników tłumienia dobiera się parametr α_Thr W momencie przekroczenia progu wykrycia następuje uruchomienie zapisu kolejnych wartości współczynników α i czasów okien do pamięci oraz uruchomienie analizy danych w celu określenia dokładniejszych granic impulsu. Za właściwy początek impulsu dobiera się chwilę t_start o największej wartości α przed zmianą znaku współczynnika tłumienia. W celu zapisywania czasów potencjalnych właściwych granic impulsu wprowadzono zmienną t_m zmienna f zawiera dotychczas największe wartości α impulsu.

W przypadku odnalezienia wartości t_start, następuje poszukiwanie końcowego właściwego krańca impulsu - t_end. Odpowiada mu najmniejsza wartość α przed ponowną zmianą znaku – tym razem na dodatni. W celu zapisywania dotychczasowych potencjalnych krańców właściwych znów wykorzystywana jest zmienna i_m. Zmienna f zawiera dotychczasowe minimalne wartości α.

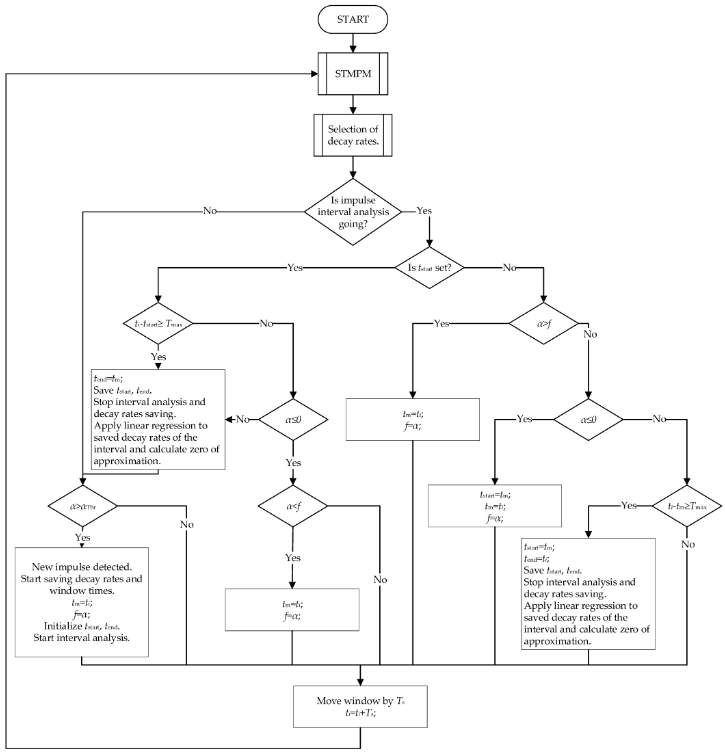
Figure 4. Residues of poles of Gaussian approximations.

W przypadku, gdy długość impulsu jest równa T_max próbek lub znaleziono jego koniec, kończy się analizę impulsu.

Charakterystykę α(t) impulsu w przedziale [t_start; t_end] próbek poddaje się aproksymacji liniowej. Współczynniki tej aproksymacji znajduje się jako rozwiązanie następującego problemu:

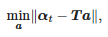
gdzie: α_t=[α(t_start),α(t_start+Ts),…,α(t_end)]^T, a=[a₁,a₀]^T

Poszukiwane współczynniki to:

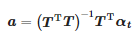
Natomiast chwila przybycia impulsu to:

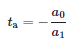
2.4. Zaadaptowany model sieci dystrybucyjnej IEEE 34

Do obliczeń zwarciowych zastosowano 34-węzłowy model sieci dystrybucyjnej IEEE w programie Simulink [23]. Jest on opracowany na podstawie rzeczywistej sieci na terenie stanu Arizona. Model uproszczono oraz zmieniono parametry na bliższe sieci stosowanych w Europie:

• zmieniono napięcie sieci z 24.9 kV na 16.5 kV,
• założono, że wszystkie odcinki linii energetycznych są liniami napowietrznymi o takich samych parametrach,
• usunięto regulatory napięć,
• założono, że obciążenia rozproszone są skupione w węzłach na dalszym krańcu części obciążonej linii,
• obciążenia są podłączone do sieci średnich napięć przez transformatory rozdzielcze,

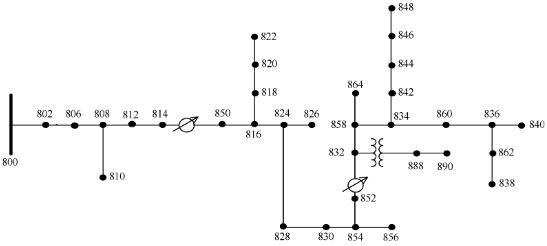
Figure 5. IEEE 34-bus Feeder topology[23].

Parametry źródła napięcia:

• częstotliwość 50 Hz,
• napięcie międzyfazowe 115.5 kV,
• rezystancja szeregowa 0.00227 Ω.
• Wymuszenie symetryczne o przesunięciu fazowych fazy L1 0°.

Parametry transformatora energetycznego:

• przekładnia 115.5/16.5;
• grupa połączeń strony górnej Yg;
• grupa połączeń strony dolnej D11;
• moc 6.3 MVA;
• napięcie zwarcia 7.5%;
• rezystancja zwarcia transformatora równa 0.49% impedancji zastępczej.

Parametry transformatorów rozdzielczych:

• przekładnia 15.75/0.4,
• grupa połączeń strony górnej D11,
• grupa połączeń strony dolnej Yg,
• moc 630 kVA,
• napięcie zwarcia 6%,
• rezystancja zwarcia transformatora równa 17.2% impedancji zastępczej.

Parametry linii elektroenergetycznej to:

• Linia trójfazowa bez przewodu neutralnego,
• jeden przewód na fazę,
• średnica przewodu 0,8466 cm,
• T/D ratio 0.311,
• DC resistance 0.5939 Ω,
• horizontal positions of conductors x=[−1,05, 0, 1,05];
• vertical positions of conductors y=[-9,05, 10,61, 9,05];
• oporność właściwa ziemi ρ=100 Ωm.

By zamodelować właściwości transformatorów w wysokich częstotliwościach do każdego z nich dołączono pojemności zgodnie z Figurą 6

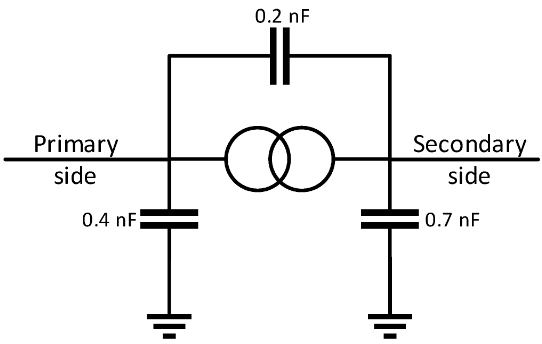
Figure 6. Transformer model.

Linie elektroenergetyczne zamodelowano w przedziale od 1 Hz do 5 MHz, uwzględniając efekt naskórkowości z wykorzystaniem Uniwersalnego Modelu Linii.

Wykonano symulacje zwarć jedno- i wielofazowych o zerowej rezystancji przejścia w 20%, 50%, 80% i 100% długości linii elektroenergetycznych, co odpowiada 76 punktom zwarcia. Kroku całkowania symulacji wynosił Δt=0,1 μs przy wykorzystaniu metody wstecznej Eulera.

3. Wyniki

3.1. Pomiary charakterystyk przenoszenia sensora SN

Pomiary charakterystyk częstotliwościowych wykonano dla sensora SN do montażu w głowicach konektorowych będącego dzielnikiem rezystancyjnym o przekładni o napięciu znamionowym pierwotnym 20/√3 kV i napięciu wtórnym 3,25/√3, co odpowiada znamionowemu współczynnikowi przenoszenia równemu:

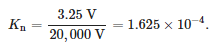
Do pomiarów wykorzystano wektorowy analizator sieciowy Bode 100 produkcji firmy OMICRON Lab. Urządzenie to umożliwia pomiary w zakresie od 1 Hz do 50 MHz. Do przeprowadzenia testów wykorzystano funkcję pomiarów wzmocnienia i fazy urządzenia opierającą się na porównaniu amplitudy i fazy sygnałów napięcia po stronie pierwotnej i wtórnej sensora. Pomiar transmitancji określonej jako stosunek napięcia po stronie wtórnej do napięcia po stronie pierwotnej wykonano dla 2048 wartości częstotliwości w zakresie od 10 Hz do 20 MHz. Przebieg zmierzonych charakterystyk pomiarowych przedstawia Figura 7.

Badany sensor napięciowy utrzymuje znamionowy współczynnik przenoszenia dla sygnałów do częstotliwości ok. 1 kHz, kiedy to charakterystyka wznosi się, aż do poziomu wzmocnienia ok. 1,84, utrzymywanego w przedziale od ok. 12,5 kHz do 6,6 MHz. Ze względu na różniczkujące działanie sensora, w strefie przejściowej – od ok. 100 Hz do 100 kHz – występuje dodatnie przesunięcie fazowe sięgające ok. 57°. W przypadku fazy możemy wyróżnić dwie strefy, dla których przesunięcie nie przekracza 6° - zakres częstotliwości do ok. 130 Hz oraz od 105 kHz do 9,4 MHz. Można więc stwierdzić, że w zakresie od 105 kHz do 6,6 MHz sygnały są przekształcane proporcjonalnie, lecz z innym współczynnikiem proporcjonalności, niż w pobliżu częstotliwości sieciowej. W przypadku zjawisk falowych zakres ten wystarcza do wiernego odwzorowania kształtu fal propagujących się w sieci [20].

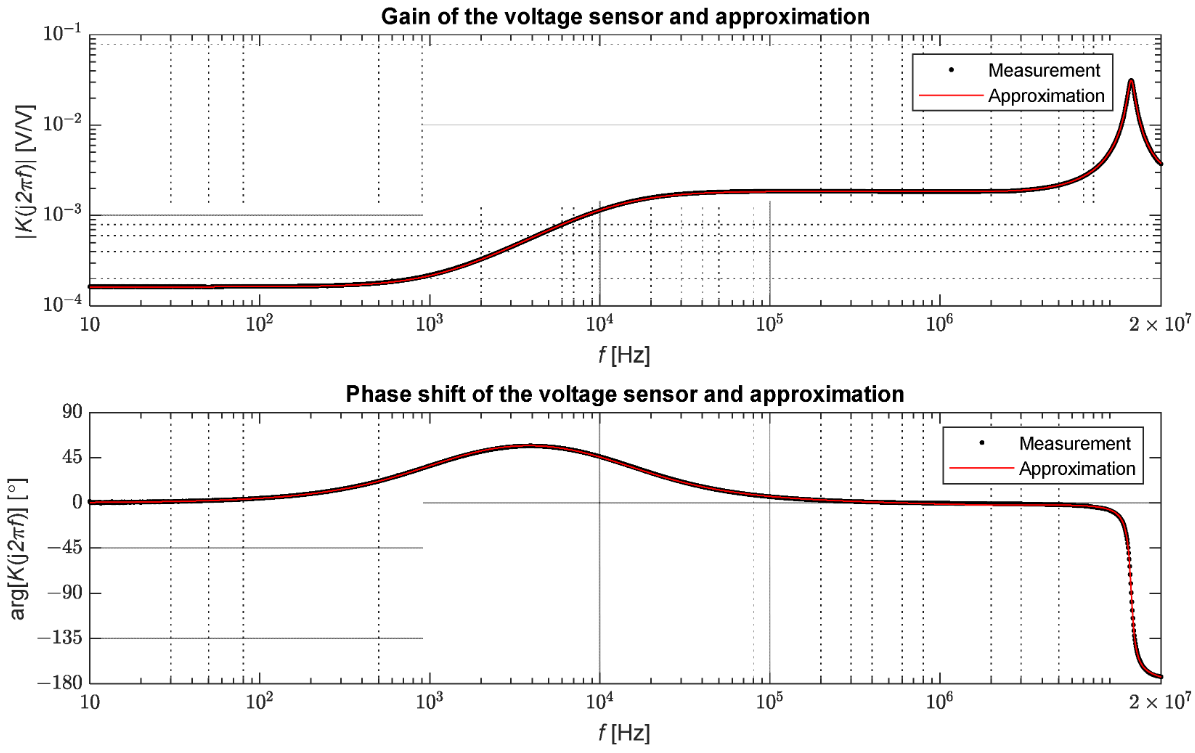
Figure 7. Wyniki pomiarów transmitancji sensora napięciowego SN.

W celu opracowania modelu matematycznego sensora, wykorzystano funkcję „tfest” programu MATLAB, by aproksymować otrzymane dane poprzez stabilną transmitancję o następującej postaci:

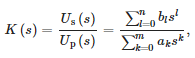
gdzie:

• U_p(s) — napięcie po stronie pierwotnej sensora,
• U_s(s) — napięcie po stronie wtórnej sensora,
• n — rząd licznika,
• m — rząd mianownika
• a_k, b_l — współczynniki wielomianów mianownika i licznika transmitancji.

Wartości współczynników transmitancji przedstawiono w Tabeli 1. Warto zwrócić uwagę, że modelowana transmitancja jest właściwa – rząd mianownika, jest większy od rzędu licznika. Na Figurze 7 również przedstawiono porównanie przebiegów uzyskanych z pomiarów z aproksymacją wzorem (1). Obliczono również średni błąd kwadratowy pomiędzy punktami pomiarowymi a aproksymacją określony następującą zależnością:

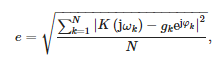
gdzie:

• N = 2048 — liczba punktów pomiarowych
• g_k — zmierzone wzmocnienie przekładnika przy pulsacji ω_k i
• φ_k — zmierzone przesunięcie fazowe przy pulsacji ω_k.

Uzyskano wartość błędu aproksymacji równą:

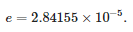
Table 1. Wartości współczynników wielomianów transmitancji zastępczej sensora napięciowego SN o budowie dzielnika rezystancyjnego.

Na Figurze 8 przedstawiono porównanie przebiegu napięcia fazowego na stacji oraz napięcia na wyjściu modelowanego sensora w przypadku bezpośredniego zwarcia trójfazowego z ziemią w węźle 816. Wyraźnie widać większe wzmocnienie przebiegów szybkozmiennych – warto zwrócić uwagę, że przebiegi te są wzmacniane w przybliżeniu proporcjonalnie.

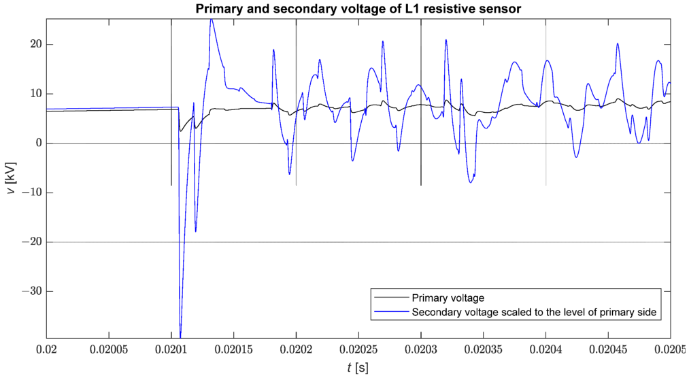
Figure 8. Porównanie przebiegu napięcia fazowego oraz napięcia na wyjściu sensora sprowadzonego na stronę pierwotną

3.2. Identyfikacja impulsów zwarciowych z pomocą KMPM

Na Figurze 9 przedstawiono przebieg wszystkich współczynników tłumienia przykładowego przebiegu napięcia na stacji elektroenergetycznej po bezpośrednim zwarciu trójfazowym z ziemią w węźle 816 modelu. Widać, że brak selekcji współczynników tłumienia utrudnia lokalizację – w szczególności odnosi się to do słabszych impulsów. Z drugiej strony, obserwacja współczynników tłumienia umożliwia łatwą identyfikację przedziałów zawierających impulsy – w przypadku wizualnej analizy przebiegu napięcia fazowego nie zawsze jest to łatwe w przypadku niewielkich amplitud impulsów.

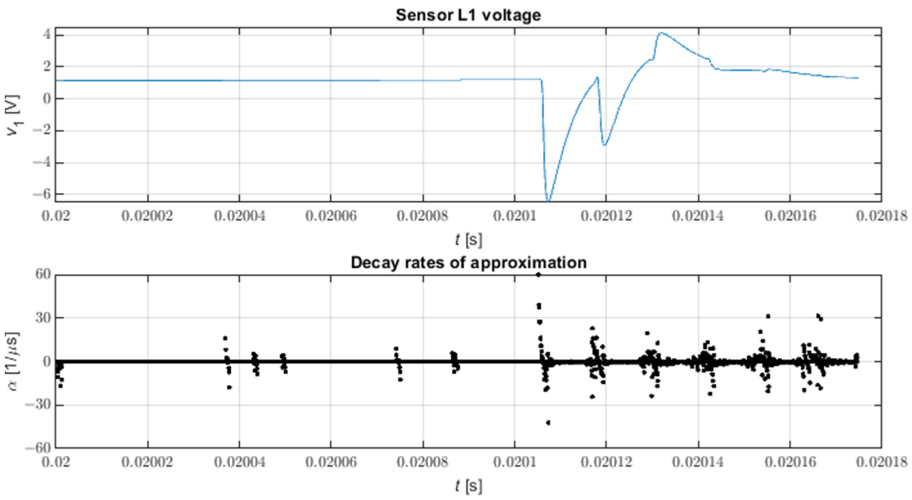
Figure 9. Współczynniki tłumienia uzyskane za pomocą KMPM. N=9, L=4.

Figura 10 przedstawia wyselekcjonowane bieguny aproksymacji wraz z przebiegiem regresji liniowej wykorzystanej do identyfikacji chwili przybycia impulsu. Odfiltrowanie niepotrzebnych współczynników tłumienia pozwala na ograniczenie liczby fałszywych wykryć impulsów.

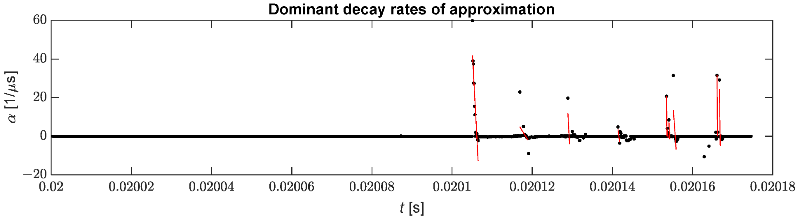
Figure 10. Wyselekcjonowane bieguny wykorzystane do identyfikacji impulsów.

W Table 2 przedstawiono wartości błędów w identyfikacji czasu przybycia pierwszej fali wędrownej do stacji. Błąd ten określa następujące równanie:

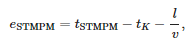
gdzie:

• t_STMPM — chwila przybycia impulsu wg KMPM,
• t_K — moment zwarcia,
• l — odległość miejsca zwarcia od stacji elektroenergetycznej
• v = 299 552 300 m/s — prędkość propagacji fali zwarciowej zmierzona dla zwarcia w najdalszym węźle (838).

Parametry metody wykorzystane do uzyskania wyników to:

• N = 5 — liczba próbek w oknie czasowym,
• L = 2 — parametr pęku macierzy,
• p = 6 — liczba znaczących liczb w wyniku pomiaru;
• α_Thr=1051s — próg wykrycia impulsu,
• T_max=2,1 μs — maksymalna szerokość impulsu,
• T_w=0,5 μs —szerokość okna,
• T_s=0,1 μs — okres próbkowania,
• r=0,02 V — próg amplitudy składowej.

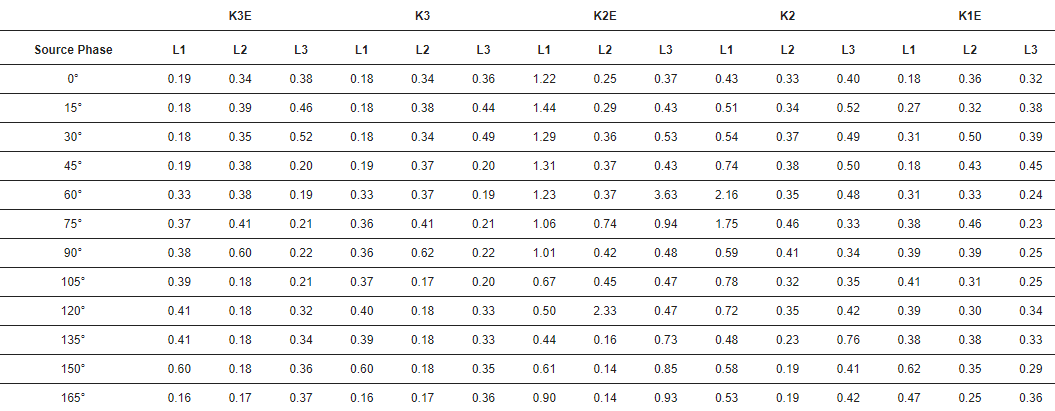
W Table 3 przedstawiono odchylenia standardowe błędu identyfikacji czasowej impulsu.

Table 2. Błąd czasowy identyfikacji impulsu w µs dla różnych rodzajów zwarć. K1E – zwarcie jednofazowe, K2 – zwarcie dwufazowe, K2E – zwarcie dwufazowe z ziemią, K3 – zwarcie trójfazowe, K3E – zwarcie trójfazowe z ziemią.

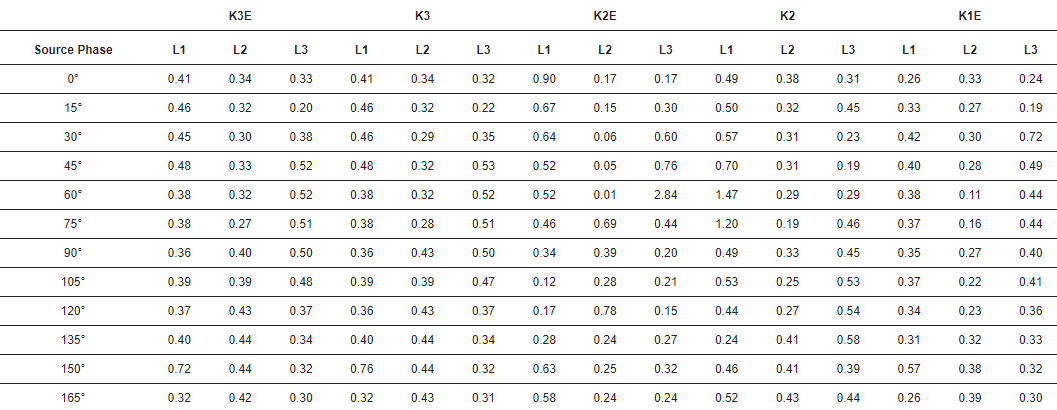
Table 3. Odchylenie standardowe błędu identyfikacji impulsu w µs. K1E – zwarcie jednofazowe fazy L1, K2 – zwarcie dwufazowe faz L1 i L2, K2E – zwarcie dwufazowe z ziemią faz L1 i L2, K3 – zwarcie trójfazowe, K3E – zwarcie trójfazowe z ziemią.

4. Dyskusja

Dzięki opracowanemu modelowi rezystancyjnego sensora napięciowego SN wykonano symulacje fal zwarciowych w modelu IEEE 34. Charakterystyka przenoszenia sensora rezystancyjnego z powodzeniem umożliwia wyszukiwanie fal zwarciowych w sygnale wtórnym. Do identyfikacji wykorzystano nowy algorytmu czasu rzeczywistego oparty na metodzie pęku macierzy. Zastosowana wariacja tejże metody charakteryzuje się wysoką precyzją identyfikacji impulsów zwarciowych – średni błąd wynosił 0,41 µs przy próbkowaniu 10 MHz. Błąd ma wartość dodatnią – znajdowany czas przybycia jest więc większy od rzeczywistego, należy jednak zwrócić uwagę, iż w praktycznych zastosowaniach metody – np. w lokalizacji falowej miejsc zwarcia, część tego błędu znosi się ze względu na specyfikę działania tych algorytmów. Dokładne identyfikowanie fal zwarciowych może umożliwić klasyfikację oraz lokalizację zwarć w sieciach średniego napięcia z wykorzystaniem tylko jednego miejsca pomiaru – szyn zbiorczych.

źródła

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Artykuł autorstwa: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).