Slenkančių bangų identifikavimas įtampos jutiklio signale vidutinės įtampos tinkle, naudojant trumpalaikį matricos pieštuko metodą

Atliekant bandymus buvo naudojamas DACPOL SP pateiktas vektorinės grandinės analizatorius Omicron-Lab Bode 100. Z O.O.

Abstrakcija

Dauguma gedimo bangų lokalizavimo metodų yra pagrįsti srovės transformatorių transformuojamos linijos srovės analize ir apsiriboja aukštos įtampos tinklais. Gedimų bangų lokalizavimas vidutinės įtampos tinkluose vis dar kuriamas. Šiame darbe pateikiamas naujas realaus laiko algoritmas, skirtas identifikuoti sklindančias bangas skirstomajame tinkle, naudojant įtampos signalą ir trumpalaikės matricos pieštuko metodą. Antrinės šoninės įtampos bangų formoms pastotėje gauti buvo sukurtas varžinio įtampos jutiklio modelis, pagrįstas plačiajuosčio ryšio matavimais nuo 10 Hz iki 20 MHz. Išbandytas jutiklis sustiprina dažnius, susijusius su keliaujančiomis bangomis, labiau nei naudingasis dažnis, leidžiantis identifikuoti. Algoritmui išbandyti buvo atlikti trumpojo jungimo modeliai IEEE 34 magistralės tiektuvu. Sukurtas metodas gali aptikti net mažos amplitudės bangas.

1. Įvadas

Maitinimo sistemos apsauga nuo gedimų yra vienas iš apsauginio perdavimo tikslų. Greitas trikdžių pašalinimas apriboja elektros įrangos daromą žalą ir sumažina jos neigiamą įtaką elektros energijos kokybei. Todėl greitų ir tikslių relių ir gedimų lokalizatorių kūrimas skirstomuosiuose tinkluose yra esminis klausimas tiek techniniu, tiek ekonominiu požiūriu. Aukštos įtampos tinkluose gedimų lokalizavimas yra paprastas, nes jiems būdinga didelė matavimų sklaida ir kilpos struktūra. Skirstomųjų tinklų atveju matavimai daugiausia atliekami viename ten esančios pastotės taške. Be to, paskirstymo tinkleliai yra medžio struktūros, todėl sugedusios šakos identifikavimas yra neaiškus. Šios problemos sprendimas gali būti keliaujančių bangų lokatorių naudojimas, kuris šiuo atveju gali būti tikslesnis nei įprasti metodai. Kad būtų galima naudoti tokius lokatorius, būtina sukurti tiksliausius keliaujančios bangos identifikavimo metodus.

Įprastas gedimų aptikimo metodas pagrįstas pagrindinio dažnio srovių ir įtampų analize. Dėl šios priežasties apsaugos algoritmai, pagrįsti tokio tipo signalais, reikalauja išanalizuoti signalo intervalą, kuris yra pakankamai ilgas, kad būtų galima įsitikinti, kad sutrikimas įvyko. Šiuolaikiškesnis požiūris pagrįstas keliaujančiomis bangomis, kurios yra aukštesnio dažnio signalai, sklindantys elektros linijomis. Tokio tipo apsauga kartais vadinama „ypač dideliu greičiu“. Jis aptinka srovės ir įtampos bangas, kurias sukelia gedimai. Tada ši apsauga nustato trikdžių tipą ir vietą, palygindama jų amplitudes ir atvykimo laiką į matavimo prietaisus. Neabejotinai pagrindinis bangomis pagrįstos apsaugos pranašumas yra veikimo greitis (mažiau nei 4 ms) [1]. Be to, jis tinkamai veikia su serijiniu būdu kompensuotomis perdavimo linijomis ir maitinimo svyravimų metu.

Gedimo vietą naudojant keliaujančias bangas galima suskirstyti į dviejų gnybtų ir vieno gnybtų schemas. Dviejų gnybtų relių atveju matavimo duomenys renkami saugomų linijų galuose ir tam reikia perduoti matavimo duomenis tarp įrenginių. Tačiau vieno gnybto relės analizuoja srovių ir įtampų signalus tik iš vieno matavimo taško. Reikia pabrėžti, kad dviejų gnybtų relės pasižymi didesniu patikimumu, nes jos naudoja tiesiogiai trikdžių generuojamas bangas, kad lokalizuotų ir klasifikuotų. Šios bangos turi didžiausią įmanomą amplitudę ir aptinkamos pirmiausia po gedimo. Tačiau vieno gnybto relių atveju apsauga grindžiama trikdžių generuojama banga ir bangomis, atsispindinčiomis nuo linijų nutrūkimų, atšakų ir paties gedimo [2]. Taip yra dėl to, kad tinkle nėra antro matavimo taško.

Aukštos įtampos tinklams būdinga tai, kad linijos galuose yra pastotės su matavimo įranga. Todėl čia naudojamos dviejų gnybtų relės. Skirstomųjų tinklų atveju aukštos/vidutinės įtampos pastotės dažniausiai yra vienintelė vieta, kur dedamos apsauginės relės su transformatoriais ar jutikliais. Tai reiškia, kad skirstomuosiuose tinkluose, naudojant viengales bangines reles, yra pigiausias sprendimas.

Paskirstymo tinkleliai yra tinklai, turintys medžio topologiją, ir dėl šios funkcijos sunku nustatyti tikslią gedimo vietą. Tiek įprastinių, tiek banginių gedimų lokalizatorių situacija yra sudėtingesnė nei perdavimo tinkluose, nes žinomu atstumu nuo pastotės gali egzistuoti kelios galimos gedimo atšakos. Sugedusi tik viena šaka. Tačiau trumpojo jungimo liniją galima nustatyti palyginus srovės bangų, išsklaidytų pastočių magistralėse amplitudes [2,3,4].

Buvo pasiūlyti įvairūs gedimų vietos nustatymo metodai, pvz., dažnių, susijusių su bangų svyravimais tarp mazgų, aptikimas [5], išmatuotos srovės palyginimas su numatoma srove tam tikroje trumpojo jungimo vietoje [6] ir tradicinius metodus, pagrįstus gedimo bangų frontų aptikimu [3,7]. Bangų frontams aptikti buvo naudojami šie metodai: bangelių transformacija, pagrindinių komponentų analizė, pagrįsta bruožų išskyrimu, Teager energijos operatorius, ansamblio empirinio režimo skaidymas ir matricinio pieštuko metodas, kuris aptariamas ir naudojamas šiame darbe [8,9]. Matricos pieštuko metodas naudojamas signalui išskaidyti į eksponentiškai slopintų sinusoidų sumą [10]. Elektros energetikos srityje matricos pieštuko metodas buvo naudojamas pagrindiniams svyravimų dėl gedimų režimams įvertinti ir harmonikoms bei subharmonikoms [11,13].

Skaitmeniniais duomenų apdorojimo algoritmais apdoroti elektros signalai į relę tiekiami stotyje esančiais matavimo prietaisais. Šie prietaisai apima srovės ir įtampos transformatorius, Rogowski rites arba jutiklius, sumažinančius elektros signalų lygį iki relėms priimtino lygio. Svarbu, kad antrinėje šių įrenginių pusėje esantis signalas būtų atkurtas kuo tiksliau ir idealiu atveju jis turėtų būti tik pakeistas. Tačiau praktikoje matavimo prietaisai turi kintamą stiprinimą ir fazės poslinkį, priklausomai nuo signalo dažnio. Prietaisas neturėtų per daug susilpninti aukštų dažnių, kad būtų galima aptikti įeinančią sklindančią bangą, kuri yra greitai kintanti bangos forma ir todėl turi aukšto dažnio komponentų. Reikia pabrėžti, kad norint tiksliai atkurti gedimo bangos amplitudę, prietaisas turi įvesti pastovų laiko delsą (pageidautina, kad jo nebūtų), o stiprinimo charakteristikos turėtų būti kuo mažiau kintančios.

Transformatoriai yra prietaisai, kurie tradiciškai naudojami elektros energijos pramonėje įtampai matuoti. Jiems būdingas labai tikslus elektros signalų transformavimas, tačiau jie turi ir trūkumų. Jie prisideda prie neigiamo ferorezonanso reiškinio, yra pažeidžiami dėl trumpųjų jungimų antrinėje grandinėje ir negali tiksliai transformuoti aukšto dažnio (>3 kHz) įtampos komponentų [14]. Štai kodėl netradiciniai jutikliai, kurių mechanizmai skiriasi nuo transformatorių sistemos, buvo sukurti kaip atsakas į poreikį tiksliai išmatuoti trumpalaikius komponentus [15,16].

Matuojant įtampą, įtampos jutikliai, pagrįsti talpiniais (C), varžiniais (R) ir varžiniais-talpiniais (RC) dalikliais, yra populiarūs netradiciniai jutikliai [14]. Visų pirma, R ir RC skirstytuvai yra populiariausi, nes jie negali sukelti ferorezonanso dėl nereikšmingo induktyvumo, tiksliai transformuoti pereinamuosius elementus ir aukštus dažnius, leidžiančius iškrauti linijoje susikaupusį krūvį ir yra atsparūs antriniams trumpiesiems jungimams. Šie skirstytuvai gali būti sėkmingai naudojami energijos kokybei matuoti ir trumpojo jungimo vietai nustatyti naudojant bangų reiškinius.

Literatūra apie įprastų transformatorių modeliavimą yra didžiulė, bet, deja, dažniausiai pateikiamos jų charakteristikų, kurių dažnis mažesnis nei 10 kHz, aprašymas [15,17]. Be to, net ir šios srities tyrimus aprašančiuose straipsniuose autoriams nepavyko rasti skaitinių Bodės grafikų duomenų ar įtampos transformatorių (tiek įprastų, tiek netradicinių) perdavimo funkcijų iki 1 MHz [19]. Tokie duomenys prieinami apie įprastą srovės transformatorių [20]. Žinoma, jutikliai skiriasi savo konstrukcija, todėl jų perdavimo charakteristikos skiriasi nuo vieno tipo iki kito, tačiau atrodo, kad reikia žinoti pavyzdžio perdavimo funkciją.

Siekiant gauti tokius duomenis, buvo atlikti vidutinės įtampos jutiklio dažninių charakteristikų matavimai. Tada jie buvo naudojami kuriant perdavimo funkcijos modelį. Tada buvo pristatytas patobulintas trumpojo laiko matricos pieštuko metodas, skirtas aptikti įtampos trumpojo jungimo bangas vidutinės įtampos tinkle, išmatuotas antrinėje įtampos jutiklių pusėje.

Straipsnio struktūra yra tokia. 2 skyriuje pateikiamas trumpalaikio matricinio pieštuko metodo aprašymas ir jo taikymas signalo impulsams rasti. Taip pat pateikiamas impulsų identifikavimo algoritmas. 3 skyriuje pateikiami įtampos jutiklio perdavimo funkcijos matavimo rezultatai ir algoritmo veikimo rezultatai, remiantis atliktais modeliavimais. Išvados pateiktos 4 skirsnyje.

2. Gedimų impulsų nustatymas vidutinės įtampos tinkle

2.1. Trumpo laiko matricos pieštuko metodas

Trumpojo laiko matricos pieštuko metodas (STPMM) apytiksliai apskaičiuoja signalą lange, kuris juda laikui bėgant, kaip sinusinių komponentų su eksponentiškai kintama amplitudė suma [10,21]:

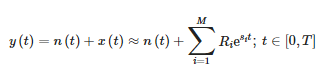
kur:

• y(t) – matavimo signalas,
• n(t) – triukšmas,
• x(t) – pradinis signalas,
• Ri – komponentų likutinė arba kompleksinė amplitudė,
• Si – sudėtingi poliai ir
• M – apytikslių komponentų skaičius.

Atrinktam signalui t = kT_s aukščiau pateikta lygtis yra tokia:

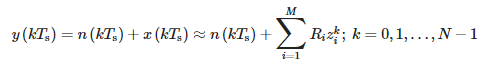
kur:

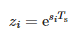
• Ts – mėginių ėmimo laikotarpis ir
• N – mėginių skaičius.

Siekiant nustatyti apytikslius parametrus, turi būti sudaryta tokia matrica:

Čia L yra pieštuko parametras. Apytikslis komponentų skaičius M atitinka šį ryšį:

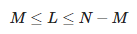
Taigi matome, kad didžiausia M vertė yra lygi ⌊N/2⌋.
Taikydami matricą Y vienaskaitos vertės skaidymui (SVD), gauname:

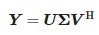
kur:

• U – (N − L) × (N − L) dydžio vienetinė matrica,
• Σ – vienaskaitos verčių stačiakampė įstrižainė matrica, kurios dydis yra (N − L) × (L + 1) ir
• V – (L + 1) × (L + 1) dydžio vienetinė matrica.

Jei išmatuotame signale nėra triukšmo, Σ matricoje būtų lygiai M nenulinis vienaskaita vertybes. Dėl triukšmo vienaskaitos reikšmės gali būti iškraipytos, o tai pasireiškia papildomomis mažomis vienaskaitos reikšmėmis. Triukšmo efektas pašalinamas pašalinus šias mažas vertes. Liko tik M dominuojančios reikšmės, kurios atitinka šią sąlygą:

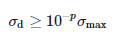
kur σ_max yra dominuojanti vienaskaitos reikšmė, o p yra tikslių reikšmingų dešimtainių matavimo skaitmenų skaičius.

Tada sudaromos gautų SVD matricų submatricos:

1. Matrica U′=[u1,u2,…,u_M], kurios dydis (N − L) × M, sukuriama paliekant stulpelius, atitinkančius vienaskaitos reikšmes, atitinkančias (7) sąlygą, ir pašalinant kiti;
2. Kvadratinė įstrižainė matrica Σ=diag(σ1,σ2,…,σM) sudaroma pašalinus Σ matricos stulpelius ir eilutes, kuriose yra vienaskaitos reikšmės, kurios neatitinka (7) sąlygos;
3. Matrica V′=[v1,v2,…,v_M], kurios dydis (L + 1) × M sudaromas paliekant stulpelius, atitinkančius vienaskaitos reikšmes, atitinkančias (7) sąlygą ir pašalinant kitus.

Tada matrica V₁′ sukuriama pašalinus paskutinę V′ matricos eilutę. V₂′ sukurta pašalinus pirmąją V′ matricos eilutę.

Tada apskaičiuojamos šios matricos:

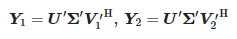
Zi reikšmės yra nenulinės apibendrintos matricų poros (Y₁, Y₂) savosios reikšmės, būtent Y savosios reikšmės ^†₁Y₂, kur Y^†₁ yra Y₁ pseudoinversija Moore–Penrose. Tada apskaičiuojame polius:

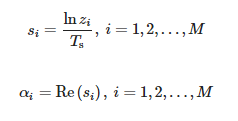
Amplitudžių reikšmes galima nustatyti taip:

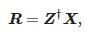
kur:

Aukščiau nurodytos operacijos atliekamos naudojant trumpalaikės matricos pieštuko metodą nuosekliems duomenų intervalams [9,22].

Apytiksliai savųjų reikšmių, pseudoinversijų ir SVD algoritmų rezultatai gali turėti įtakos zi vertėms, kurios skiriasi nuo nulio, nors artimos nuliui. Šios reikšmės turi įtakos MPM greičiui ir gali neigiamai paveikti jų rezultatus, todėl prieš apskaičiuojant likučius verta jas pašalinti.

2.2. Komponentinių polių elgesys pulso apylinkėse

Dėl elektros tinklo gedimų generuojami impulsai, sklindantys elektros linijomis artimu šviesos greičiui [3]. Šiuos impulsus galima nustatyti naudojant STMPM aproksimacijos polių poslinkio analizę. 1 paveiksle pavaizduoti trys Gauso formos impulsų pavyzdžiai ir jų aproksimacijos su STMPM poliai. Kai ateina impulsas, aproksimacija su eksponentiniais komponentais keičiasi judant laiko langui. Kai impulsas yra į dešinę nuo vidurinio lango taško, aproksimacijos poliai turi teigiamą realiąją dalį, kai Gauso viršūnė yra lango viduryje, tikroji polių dalis yra artima nuliui, o kai impulsas yra pirmoje lango pusėje, poliai turi neigiamą realiąją dalį. Todėl tikrosios polių dalies ženklo pokytis rodo, kad impulso centras perėjo per atrankos lango vidurinį tašką [22]. Taip pat iš 2 paveikslo matome, kad poliai, turintys didžiausią tikrosios dalies absoliučią vertę (taigi ir didžiausią amplitudės keitimo greitį), turi didžiausią pradinio amplitudės modulio (likučio) reikšmę.

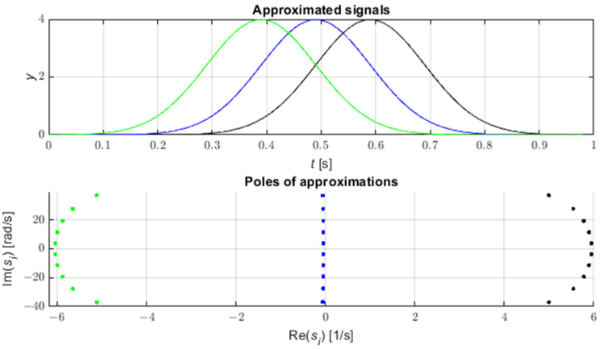
1 pav. Gausas ir atitinkami aproksimacijų poliai.

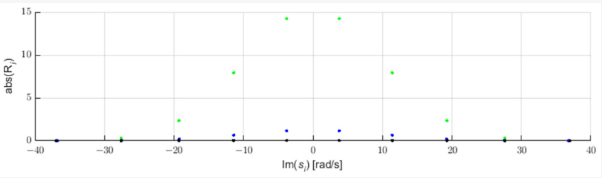
2 pav. Gauso aproksimacijų komponentų liekanos.

Taigi matome, kad impulso viršūnės laiko koordinatę galima apytiksliai identifikuoti su slopinimo koeficientų ženklo pasikeitimo momentu.

Gavę nuo laiko priklausomą šių koeficientų eigą naudodami STMPM, galime juos taikyti tiesiniu aproksimavimu šalia taško, kuriame koeficientai eina per nulį, ir gauti apytikslę viršutinę impulso koordinatę. Pažymėtina, kad didžiausiu kintamumu pasižymintys koeficientai pasižymi ir didžiausia amplitude – jie yra didžiausi impulso komponentai.

2.3. Impulsų aptikimo realiuoju laiku algoritmas

Impulsų, kylančių iš sklindančių bangų, aptikimo algoritmo struktūrinė schema parodyta 3 paveiksle. Algoritmas paeiliui perduoda signalo langus STMPM, kad išskirtų aproksimavimo komponentų nykimo greitį.

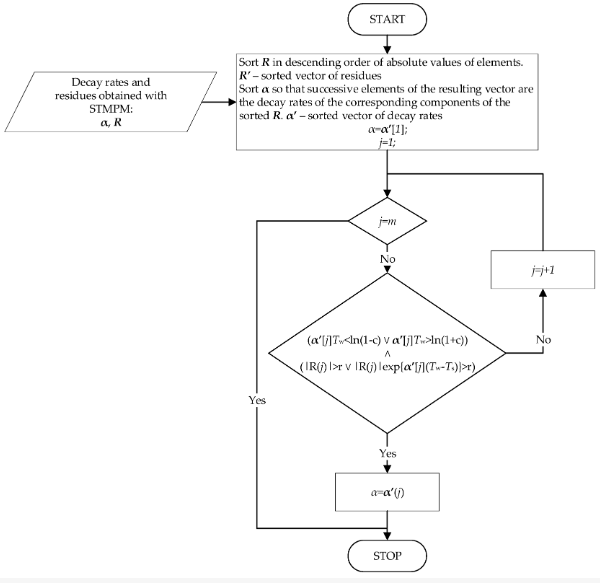
3 pav. Mažėjimo greičio pasirinkimo algoritmas.

Gauti komponentai yra atrenkami, kurių procedūra parodyta 4 pav. Atranka remiasi prielaida, kad didžiausios amplitudės STMPM komponentai turi būti imami piko laikui. aproksimacija – jie sudaro didžiausią indėlį į trumpalaikį signalo komponentą. Tai atitinka ankstesnio punkto stebėjimą – didžiausią amplitudės pokytį turintiems komponentams būdinga didžiausia pradinė amplitudė. Tuo atveju, kai didžiausios amplitudės komponentui būdingas mažas slopinimo greitis per visą T_w ilgio langą – mažesnis už parametrą c – arba jos didžiausias indėlis į signalą yra mažesnis nei r, kitas komponentas pagal amplitudės dydį pasirenkamas kaip potencialus skilimo greičio α kandidatas. Kartodami šią procedūrą kitiems komponentams, kol bus įvykdyta sąlyga, galiausiai gaunamas koeficientas α, kuris tada naudojamas apytiksliai impulso atvykimo laikui apskaičiuoti. Jei nė vienas komponentas neatitinka pirmiau nurodytų sąlygų, pasirenkamas tas, kurio amplitudė yra didžiausia.

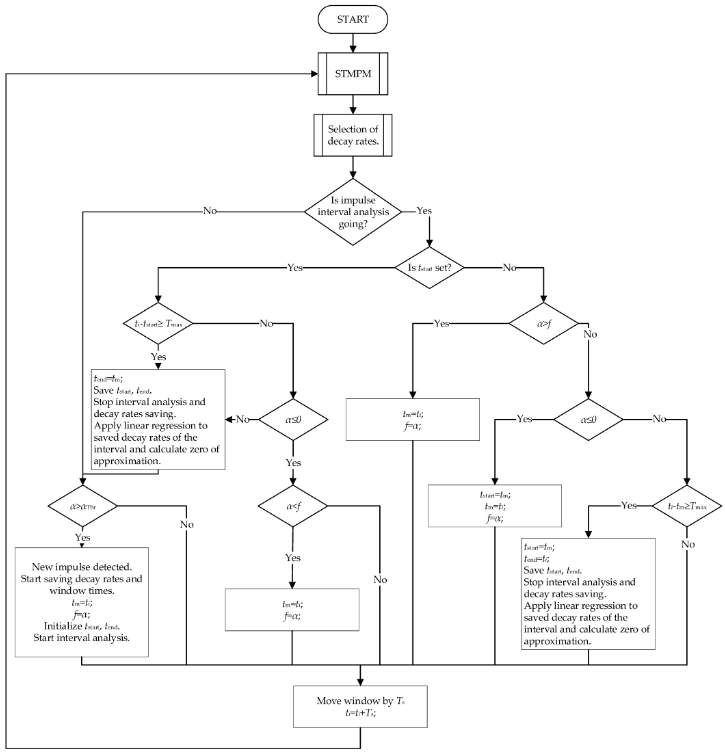
4 pav. Impulsų identifikavimo algoritmas.

Laikas, susietas su langu, yra:

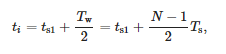
kur t_s1 – pirmojo lango pavyzdžio laikas ir T_w – lango plotis.

Impulso atėjimą rodo staigus α dažnių padidėjimas, susijęs su greitu signalo pasikeitimu mėginių ėmimo lango pabaigoje. Parametras α_Thr pasirenkamas kaip mažėjimo greičio slenkstis. Viršijus aptikimo slenkstį, į atmintį įrašomos vėlesnės α koeficientų reikšmės ir lango laikas, pradedama duomenų analizė, siekiant nustatyti tikslesnes impulsų ribas. Momentas t_start su didžiausia α reikšme prieš pakeičiant mažėjimo greičio ženklą pasirenkamas kaip tinkama impulso pradžia. Siekiant išsaugoti galimus teisingų impulsų ribų laikus, kintamasis t_m buvo įvestas su kintamuoju f, kuriame yra didžiausios iki šiol apskaičiuotos impulso α reikšmės.

Jei randama t_start reikšmė, pradedama ieškoti galutinės tinkamo impulso t_end pabaigos. Tai atitinka mažiausią α reikšmę prieš vėl pasikeičiant ženklui, šį kartą į teigiamą. Kintamasis i_m vėl naudojamas ankstesniems galimiems galutiniams taškams išsaugoti. Kintamajame f yra ankstesnės minimalios α reikšmės.

Kai impulso ilgis yra lygus mėginių T_max arba randamas impulso pabaiga, impulso analizė nutraukiama.

Funkcija α(t) intervale [t_pradžia; t_end] taikoma tiesinė regresija. Šios regresijos koeficientai randami kaip šios problemos sprendimas:

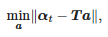
kur: α_t=[α(t_pradžia), α(t_pradžia+Ts),…,α(t_pabaiga)]^T, a=[a₁,a₀]^T

Ieškomi koeficientai yra:

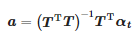
Kadangi impulso atvykimo momentas yra:

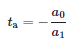
2.4. Pritaikytas IEEE 34 magistralės bandomasis tiektuvas

Trumpojo jungimo skaičiavimams buvo sukurtas 34 magistralių IEEE bandomasis tiekimo modelis Simulink. Tiektuvo topologija parodyta 5 pav. [23]. Tiektuvas yra pagrįstas tikru tinklu Arizonos valstijoje. Tai pakankamai paprasta, kad netaptų didele skaičiavimo našta atliekant trumpalaikius modeliavimus su nedideliu integravimo žingsniu. Modelis buvo supaprastintas, o parametrai pakeisti taip, kad būtų imituojami Europos tinkleliai:

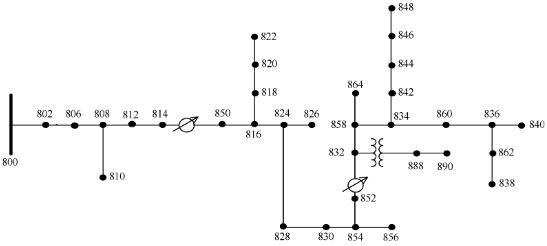
5 pav. IEEE 34 magistralės tiektuvo topologija.

• Tinklo įtampa pakeista iš 24,9 kV į 16,5 kV;
• Laikyta, kad visos elektros linijų dalys yra oro linijos su tais pačiais parametrais;
• Įtampos reguliatoriai buvo pašalinti;
• Manoma, kad paskirstytos apkrovos susikaupė autobusuose, esančiuose tolimiausiame apkrautų linijų gale;
• Apkrovos buvo prijungtos prie vidutinės įtampos tinklo per skirstomuosius transformatorius;
• Aukštos / vidutinės įtampos transformatoriaus nulinis taškas buvo atjungtas nuo įžeminimo.

Įtampos šaltinio parametrai:

• 50 Hz dažnis;
• 115,5 kV linijos įtampa;
• Atsparumas 0,00227 Ω.
• Simetrinis šaltinis, kurio L1 fazės poslinkis lygus 0°.

Galios transformatoriaus parametrai:

• Įtampos santykis 115,5/16,5;
• Aukštos įtampos apvijos Yg vektorių grupė;
• Žemos įtampos apvijos D11 vektorių grupė;
• 6,3 MVA galia;
• Santykinė trumpojo jungimo įtampa 7,5 %;
• Atsparumas trumpajam jungimui, lygus 0,49 % ekvivalentinės varžos.

Paskirstymo transformatorių parametrai:

• Įtampos santykis 15,75/0,4;
• Aukštos įtampos apvijos D11 vektorių grupė;
• Žemos įtampos apvijos Yg vektorių grupė;
• Galingumas 630 kVA;
• Santykinė trumpojo jungimo įtampa 6 %;
• Atsparumas trumpajam jungimui, lygus 17,2 % ekvivalentinės varžos.

Elektros linijų parametrai:

• Trifazė linija be neutralės;
• Vienas laidininkas vienoje fazėje;
• Laidžio skersmuo 0,8466 cm;
• T/D santykis 0,311;
• Nuolatinės srovės varža 0,5939 Ω/km;
• Laidžių horizontalios padėties x=[−1,05, 0, 1,05];
• Vertikalios laidininkų padėtys u=[−9,05, 10,61, 9,05];
• Įžeminimo varža ρ=100 Ωm.

Prie kiekvieno transformatoriaus buvo prijungtos talpos, kaip parodyta 6 paveiksle [5] in. siekiant modeliuoti transformatorių savybes aukštuose dažniuose.

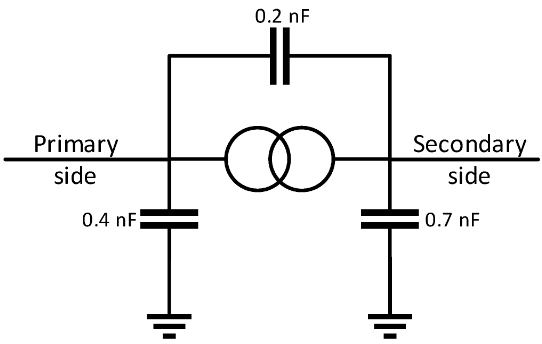
6 pav. Transformatoriaus modelis.

Maitinimo linijos buvo modeliuojamos nuo 1 Hz iki 1 MHz, atsižvelgiant į odos efektą naudojant universalųjį linijos modelį.

Vienfazių ir daugiafazių trumpųjų jungimų su nuline kryžmine varža modeliavimas buvo atliktas 20%, 50%, 80% ir 100% linijų ilgio. Tai atitinka 76 trumpojo jungimo vietas. Modeliavimo integravimo žingsnis buvo Δt=0,1 μs. Tustin / Backward Euler buvo naudojamas integravimo metodas.

3. Rezultatai

3.1. Vidutinės įtampos jutiklio perdavimo charakteristikų matavimai

Dažnio atsako matavimai buvo atlikti vidutinės įtampos jutikliui, skirtam montuoti jungčių galvutėse. Jutiklis buvo varžinis daliklis, kurio vardinė pirminė įtampa 20/√3 kV ir vardinė antrinė įtampa 3,25/√3, o tai atitinka įtampos santykį:

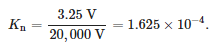
Matavimams buvo naudojamas OMICRON Lab's Bode 100 vektorinis tinklo analizatorius. Šiuo įrenginiu galima atlikti matavimus nuo 1 Hz iki 50 MHz. Atliekant bandymus buvo naudojama įrenginio stiprinimo ir fazės matavimo funkcija. Ši funkcija buvo pagrįsta pirminės ir antrinės jutiklio pusėse esančių įtampos signalų amplitudės ir fazės palyginimu. Perdavimo funkcijos matavimas, apibrėžiamas kaip antrinės pusės įtampos ir pirminės pusės įtampos santykis, buvo atliktas 2048 dažnio vertėms diapazone nuo 10 Hz iki 20 MHz. Išmatuotos vertės pateiktos 7 pav.

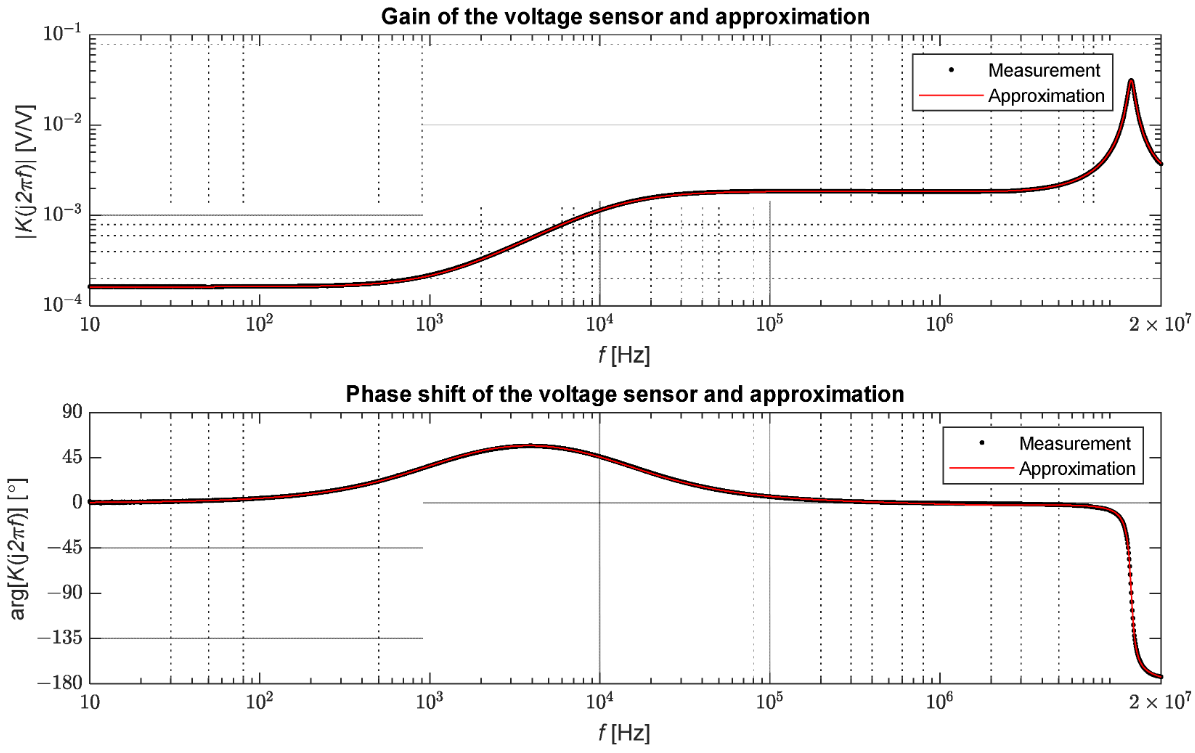
7 pav. Vidutinės įtampos jutiklio pralaidumo matavimo rezultatai.

Išbandytas įtampos jutiklis palaiko vardinį signalų perdavimo koeficientą iki maždaug 1 kHz dažnio, tada grafikas pakyla iki maždaug 1,84 × 10⁻³ stiprinimo lygio; šis lygis palaikomas nuo maždaug 12,5 kHz iki 6,6 MHz. Dėl skirtingos jutiklio savybės pereinamojoje zonoje nuo 100 Hz iki 100 kHz yra maždaug 57° teigiamas fazės poslinkis. Fazės atveju galime išskirti dvi zonas, kurių poslinkis neviršija 6°. Šiuo atveju dažnių diapazonas yra maždaug iki 130 Hz ir nuo 105 kHz iki 9,4 MHz. Todėl galima daryti išvadą, kad diapazone nuo 105 kHz iki 6,6 MHz, ir signalai yra proporcingai transformuojami, bet su kitokiu proporcingumo koeficientu nei šalia tinklo dažnio. Bangų reiškinių atveju šio diapazono pakanka, kad būtų tiksliai atvaizduota tinkle sklindančių bangų forma [20]. Verta paminėti, kad skirtingos konstrukcijos įtampos jutikliai gali turėti skirtingas perdavimo savybes.

Siekiant sukurti matematinį jutiklio modelį, MATLAB funkcija „tfest“ buvo naudojama duomenims, gautiems naudojant stabilią šios formos perdavimo funkciją, apytiksliai įvertinti:

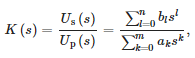
kur:

• Up(s) – įtampa pirminėje jutiklio pusėje,
• Us (-iai) – įtampa antrinėje jutiklio pusėje,
• n – skaitiklio tvarka,
• m – vardiklio ir
tvarka
• ak, bl – pralaidumo vardiklio ir skaitiklio daugianario koeficientai iš eilės.

Perdavimo funkcijos koeficientų reikšmės pateiktos 1 lentelėje. Verta pažymėti, kad sumodeliuotas pralaidumas yra tinkamas, nes vardiklio tvarka yra didesnė už skaitiklio eilę. 7 paveiksle taip pat parodytas perdavimo funkcijų, gautų iš matavimų, palyginimas su aproksimacija pagal formulę (19). Taip pat buvo apskaičiuota vidutinė kvadratinė paklaida tarp matavimo taškų ir aproksimacija, nustatyta pagal šį ryšį:

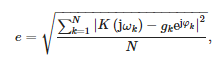
kur:

• N = 2048 – matavimo dažnių skaičius
• g_k – išmatuotas jutiklio stiprinimas pulsuojant ω_k ir
• φ_k – išmatuotas jutiklio fazės poslinkis pulsuojant ω_k.

Apytikslė klaidos reikšmė yra lygi:

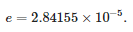
1 lentelė. Įtampos jutiklio su varžine daliklio struktūra ekvivalentinio pralaidumo daugianario koeficientų reikšmės.

8 paveiksle parodytas fazinės įtampos bangos formos pastotėje palyginimas, gautas atliekant modeliavimą, ir įtampos modeliuoto jutiklio išėjime, esant tiesioginiam trifaziui trumpajam jungimui su įžeminimu 816 mazge. aiškiai matoma, kad greitųjų pereinamųjų procesų stiprinimas yra didesnis nei lėtųjų. Verta paminėti, kad šios bangos formos sustiprinamos beveik proporcingai.

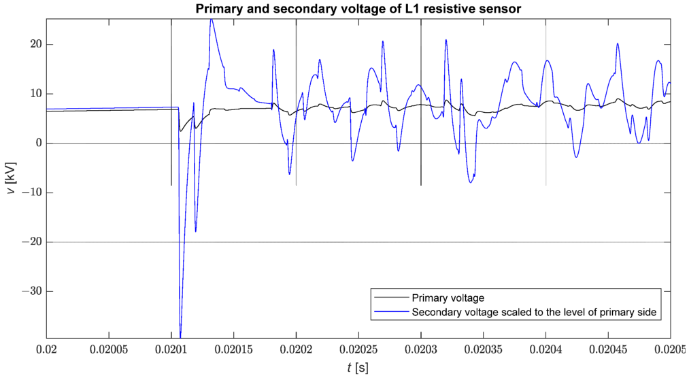
8 pav. Fazinės įtampos bangos formos (v_L1) ir jutiklio išėjimo įtampos palyginimas pagal pirminę įtampą (v_L1/K_n) gedimo metu.

3.2. Trumpojo jungimo impulsų identifikavimas naudojant STMPM

9 paveiksle parodyta visų pavyzdinės įtampos bangos formos slopinimo greičių bangos forma pastotėje po trifazio nulinės varžos trumpojo jungimo su žeme modelio 816 mazge. Galima pastebėti, kad dėl skilimo greičio pasirinkimo trūkumo impulsus sunku rasti; tai ypač pasakytina apie silpnesnį impulsą. Kita vertus, vizualinis slopinimo greitis leidžia lengvai nustatyti intervalus, kuriuose yra impulsų, vizualiai analizuojant fazinės įtampos bangų formas, nors tai ne visada lengva esant mažoms impulsų amplitudėms.

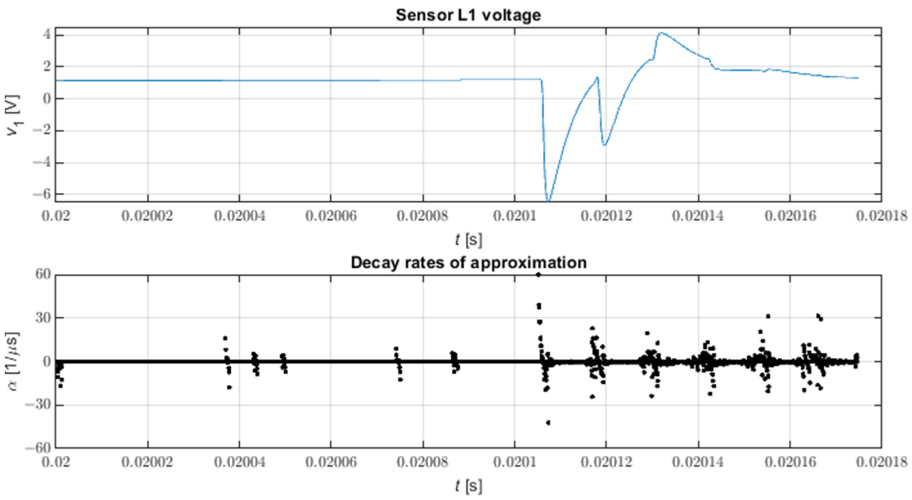
9 pav. Visi STMPM aproksimacijos mažėjimo laipsniai. N = 9, L = 4.

10 paveiksle pavaizduoti pasirinkti slopinimo laipsniai kartu su tiesine regresija, naudojama impulso atvykimo momentui nustatyti. Klaidingų impulsų aptikimų skaičių galima sumažinti išfiltravus nereikalingus silpninimo koeficientus.

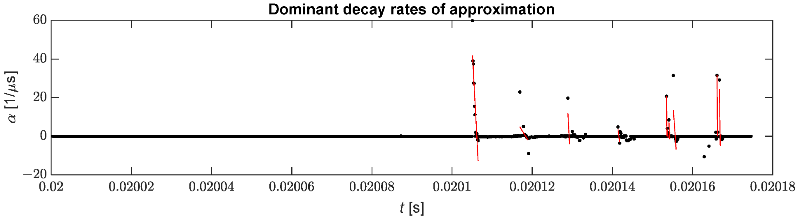
10 pav. Impulsų identifikavimui naudojami pasirinkti slopinimo laipsniai.

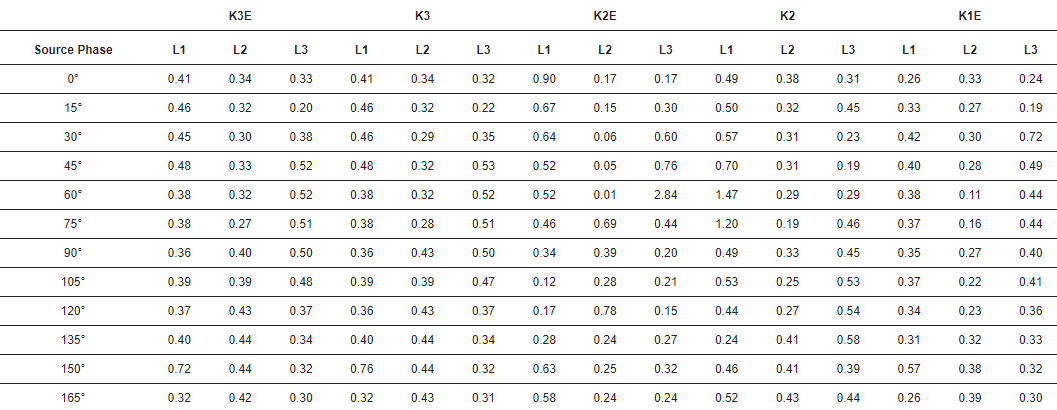
2 lentelėje parodytos klaidos nustatant pirmosios įeinančios bangos atvykimo laiką į stotį. Ši klaida apibrėžiama pagal šią lygtį:

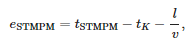
kur:

• t_STPMM – atvykimo momentas pagal STMPM,
• t_K – gedimo momentas,
• l —trumpojo jungimo vietos atstumas nuo pastotės ir
• v = 299 552 300 m/s – gedimo bangų sklidimo greitis, išmatuotas dėl trumpojo jungimo tolimiausiame mazge (838).

Rezultatams gauti naudojami metodo parametrai:

• N = 5 – mėginių skaičius per laiko langelį;
• L = 2 – pieštuko parametras;
• p = 6 – tikslių reikšmingų dešimtainių matavimo skaitmenų skaičius;
• α_Thr=1051s – impulso aptikimo slenkstis;
• T_maks.=2,1 μs – didžiausias impulso plotis;
• T_w=0,5 μs – lango plotis;
• T_s=0,1 μs – mėginių ėmimo laikotarpis;
• r=0,02 V – amplitudės slenkstis.

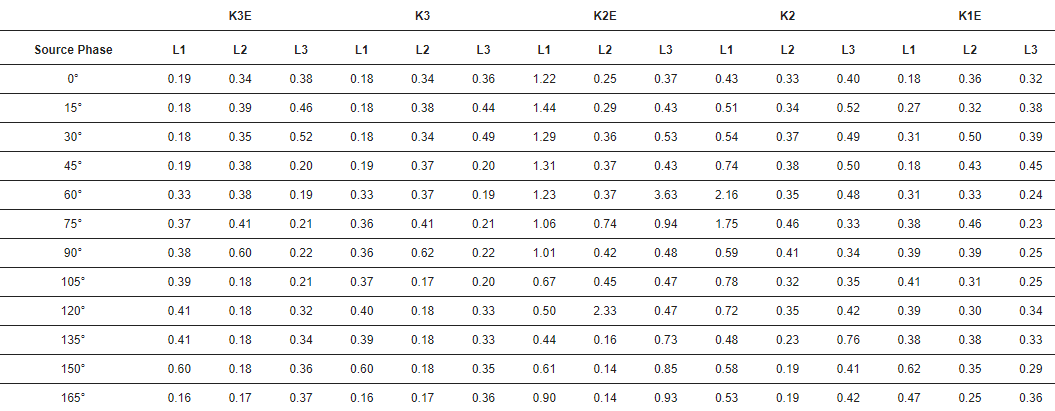
3 lentelėje rodomi standartiniai impulso laiko paklaidos nuokrypiai.

2 lentelė. Laikinoji bangos identifikavimo paklaida skirtingų gedimų atveju. Matavimo vienetas: µs. K3E – trijų fazių ir žemės gedimas, K3 – trijų fazių gedimas, K2E – dviejų fazių ir žemės gedimas, K2 – dviejų fazių gedimas, K1E – fazės ir žemės gedimas.

3 lentelė. Standartinis laiko paklaidos nuokrypis. Matavimo vienetas: µs. K3E – trijų fazių ir žemės gedimas, K3 – trijų fazių gedimas, K2E – dviejų fazių ir žemės gedimas, K2 – dviejų fazių gedimas, K1E – fazės ir žemės gedimas.

4. Diskusija

Sukurtas varžinio įtampos jutiklio perdavimo funkcijos modelis, pagrįstas plačiajuosčio ryšio matavimais nuo 10 Hz iki 20 MHz. IEEE 34 magistralės modelio gedimų generuojamų važiuojančių bangų modeliavimas buvo atliktas naudojant perdavimo funkciją. Rezistinio jutiklio dažnio atsako pakako antrinės įtampos signalo gedimo bangoms identifikuoti. Jutiklis transformuoja slenkančių bangų signalus su maždaug pastoviu stiprėjimu, kuris yra didesnis nei naudingumo dažnio stiprinimas. Identifikavimui buvo naudojamas naujas realaus laiko algoritmas, pagrįstas matricinio pieštuko metodu. Straipsnyje panaudotas šio metodo variantas pasižymi dideliu bangų identifikavimo tikslumu, nes imant 10 MHz dažnių atranką vidutinė paklaida buvo 0,41 µs, o paklaida turėjo teigiamą reikšmę, todėl rastas atvykimo laikas buvo didesnis nei tikrasis. Tačiau reikia pažymėti, kad taikant metodą praktikoje, pvz., gedimų lokalizavime bangomis, šios klaidos dalis eliminuojama dėl diferencinio šių algoritmų veikimo. Tikslus gedimų bangų nustatymas leidžia klasifikuoti ir lokalizuoti gedimus vidutinės įtampos tinkluose, naudojant šynas kaip vienintelį matavimo tašką. Norint patikrinti algoritmo efektyvumą ir palyginti jį su kitais įeinančių bangų impulsų atpažinimo metodais, reikalingas testas naudojant tikrus signalus. Gana teisinga įtampos transformacija jutikliais gali leisti klasifikuoti gedimo tipą pagal jų generuojamų bangų amplitudes.

Nuorodos

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Straipsnis pagal: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).