Идентификация бегущих волн в сигнале датчика напряжения в сети среднего напряжения с использованием метода краткосрочного матричного карандаша

Аннотация

В тестах использовался векторный анализатор цепей Omicron-Lab Bode 100, предоставленный DACPOL SP. З О.О.

Большинство методов локализации волны неисправности основаны на анализе линейного тока, преобразованного трансформаторами тока, и ограничены высоковольтными сетями. Локализация волны повреждения в сетях среднего напряжения все еще находится в стадии разработки. В данной статье представлен новый алгоритм идентификации бегущих волн в распределительной сети в режиме реального времени с использованием сигнала напряжения и метода краткосрочного матричного карандаша. Для получения осциллограмм напряжения вторичной стороны на подстанции была разработана модель резистивного датчика напряжения на основе широкополосных измерений от 10 Гц до 20 МГц. Тестируемый датчик усиливает частоты, связанные с бегущими волнами, больше, чем частота сети, что позволяет проводить идентификацию. Для проверки алгоритма было выполнено моделирование короткого замыкания на фидере 34-шины IEEE. Разработанный метод позволяет обнаруживать волны даже малой амплитуды.

1. Введение

Защита энергосистемы от неисправностей является одной из задач релейной защиты. Быстрое устранение возмущения ограничивает ущерб, наносимый энергетическому оборудованию, и снижает его негативное влияние на качество электроэнергии. Поэтому разработка быстрых и точных реле и устройств обнаружения повреждений в распределительных сетях является ключевым вопросом как с технической, так и с экономической точки зрения. В случае сетей высокого напряжения локализация повреждений проста, так как они характеризуются большим разбросом измерений и петлевой структурой. В случае распределительных сетей измерения в основном производятся в одной точке подстанции. Кроме того, распределительные сети имеют древовидную структуру, что затрудняет идентификацию неисправных ветвей. Решением этой проблемы может стать использование локаторов бегущей волны, которые в этом случае могут быть более точными, чем традиционные методы. Для того чтобы использование таких локаторов стало возможным, необходимо разработать максимально точные методы идентификации бегущей волны.

Традиционный подход к обнаружению неисправностей основан на анализе токов и напряжений основной частоты. По этой причине алгоритмы защиты, основанные на этих типах сигналов, требуют анализа достаточно продолжительного интервала сигнала, чтобы убедиться, что помеха возникла. Более современный подход основан на бегущих волнах, которые представляют собой высокочастотные сигналы, распространяющиеся по линиям электропередач. Этот тип защиты иногда называют «сверхскоростной». Он обнаруживает волны тока и напряжения, генерируемые неисправностями. Затем эта защита определяет как тип, так и место возмущения на основе сравнения их амплитуд и времени прихода к измерительным приборам. Безусловно, ключевым преимуществом волновой защиты является скорость работы (менее 4 мс) [1]. Более того, он корректно работает с линиями передачи с последовательной компенсацией и при скачках мощности.

Локализация повреждений с помощью бегущих волн может быть разделена на двухполюсные и однополюсные схемы. В случае двухполюсных реле сбор данных измерений происходит на концах защищенных линий и требует передачи данных измерений между устройствами. Однако однополюсные реле анализируют сигналы токов и напряжений только с одной точки измерения. Следует подчеркнуть, что двухполюсные реле характеризуются более высокой надежностью, поскольку они используют волны, непосредственно генерируемые возмущением, для его локализации и классификации. Эти волны имеют максимально возможную амплитуду и обнаруживаются первыми после неисправности. Однако в случае однополюсных реле защита основана на волне, генерируемой помехой, и на волнах, отраженных от разрывов линии, ответвлений и самой неисправности [2]. Это связано с отсутствием второй точки измерения в сети.

Для высоковольтных сетей характерно наличие подстанций с приборами учета на концах линий. Поэтому здесь используются двухполюсные реле. В случае распределительных сетей подстанции высокого/среднего напряжения обычно являются единственным местом, где размещаются реле защиты с трансформаторами или датчиками. Это означает, что в распределительных сетях использование однотактных волновых реле является самым дешевым решением.

Распределительные сети представляют собой сети с древовидной топологией, и эта функция затрудняет точное определение местоположения неисправности. Как для обычных, так и для волновых локаторов повреждений ситуация более сложная, чем в передающих сетях, поскольку на известном расстоянии от подстанции может существовать несколько потенциальных поврежденных ветвей. Повреждена только одна из ветвей. Однако короткозамкнутую линию можно определить путем сравнения амплитуд волн тока, рассеянных на шинах подстанции [2,3,4].

Были предложены различные методы обнаружения неисправностей, такие как обнаружение частот, связанных с колебаниями волн между узлами [5], сравнение измеренного тока с прогнозируемым для данного места короткого замыкания [6] и более традиционные методы, основанные на обнаружении фронтов волн разломов [3,7]. Для обнаружения волновых фронтов использовались следующие методы: вейвлет-преобразование, анализ главных компонент, основанный на извлечении признаков, оператор энергии Тигера, ансамблевая эмпирическая модовая декомпозиция и метод матричного карандаша, который обсуждается и используется в этой статье [8,9]. Метод матричного карандаша используется для разложения сигнала на сумму экспоненциально затухающих синусоид [10]. В области электроэнергетики метод матричного карандаша использовался для оценки основных форм колебаний, вызванных неисправностями, а также для оценки гармоник и субгармоник [11,12,13].

Электрические сигналы, обработанные алгоритмами цифровой обработки данных, поступают на реле с помощью измерительных устройств, расположенных на станции. К таким устройствам относятся трансформаторы тока и напряжения, пояса Роговского или датчики, снижающие уровень электрических сигналов до уровня, приемлемого для реле. Важно, чтобы сигнал на вторичной стороне этих устройств воспроизводился максимально точно и в идеале он должен быть только масштабирован. На практике, однако, измерительные приборы имеют переменное усиление и фазовый сдвиг в зависимости от частоты сигнала. Прибор не должен слишком сильно ослаблять высокие частоты, чтобы иметь возможность обнаруживать входящую бегущую волну, которая имеет быстро меняющуюся форму и, следовательно, содержит высокочастотные компоненты. Следует подчеркнуть, что для точного воспроизведения амплитуды волны разлома прибор должен вводить постоянную временную задержку (желательно вообще никакой), а его характеристики усиления должны как можно меньше изменяться.

Трансформаторы — это приборы, которые традиционно используются в электроэнергетике для измерения напряжения. Они характеризуются очень точным преобразованием электрических сигналов, но имеют и недостатки. Они способствуют негативному явлению феррорезонанса, подвержены повреждениям, вызванным короткими замыканиями во вторичной цепи, и не способны точно преобразовывать высокочастотные (>3 кГц) составляющие напряжения [14]. Поэтому в ответ на необходимость точного измерения переходных составляющих [15,16].

Для измерения напряжения популярны датчики напряжения на основе емкостных (C), резистивных (R) и резистивно-емкостных (RC) делителей [14]. В частности, делители R и RC являются наиболее популярными, поскольку они не могут индуцировать феррорезонанс из-за незначительной индуктивности, точно преобразовывают переходные процессы и высокие частоты, позволяя разряжать накопленный заряд в линии и устойчивы к коротким замыканиям на вторичной стороне. Эти делители можно успешно использовать для измерения качества электроэнергии и для определения местоположения коротких замыканий с помощью волновых явлений.

Литература по моделированию обычных трансформаторов обширна, но, к сожалению, обычно речь идет об описании их характеристик на частотах ниже 10 кГц [15,17]. Более того, авторы не смогли найти численные данные диаграмм Боде или передаточных функций трансформаторов напряжения (как обычных, так и нетрадиционных) до 1 МГц даже в статьях, описывающих исследования в этой области [18,19]. Такие данные доступны для обычного трансформатора тока [20]. Конечно, датчики различаются по конструкции, что приводит к вариациям их передаточных характеристик от одного типа к другому, но представляется необходимым знать передаточную функцию примера.

Для получения таких данных были проведены измерения частотных характеристик датчика среднего напряжения. Затем они были использованы для разработки модели передаточной функции. Затем был представлен усовершенствованный метод краткосрочного матричного карандаша применительно к обнаружению волн короткого замыкания напряжения в сети среднего напряжения, измеренных на вторичной стороне датчиков напряжения.

Структура статьи следующая. В разделе 2 дается описание метода кратковременного матричного карандаша с его применением для нахождения сигнальных импульсов. Также предусмотрен алгоритм идентификации импульсов. Раздел 3 содержит результаты измерений передаточной функции датчика напряжения и результаты работы алгоритма на основе проведенного моделирования. Выводы приведены в Разделе 4.

2. Идентификация импульсов неисправности в сети среднего напряжения

2.1. Краткосрочный матричный карандашный метод

Метод краткосрочного матричного карандаша (STMPM) аппроксимирует сигнал внутри окна, который перемещается во времени как сумму синусоидальных составляющих с экспоненциально изменяющейся амплитудой [10,21]:

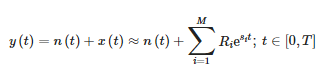
где:

• y(t) — сигнал измерения,
• n(t) — шум,
• x(t) — исходный сигнал,
• Ri — невязки или комплексные амплитуды компонентов,
• Si — комплексные полюса и
• M — количество компонентов аппроксимации.

Для дискретизированного сигнала t = kT_s приведенное выше уравнение принимает следующий вид:

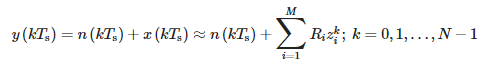
где:

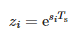
• Ts — период выборки и
• N – количество образцов.

Для определения параметров аппроксимации строится следующая матрица:

Здесь L — параметр карандаша. Количество компонентов аппроксимации M удовлетворяет следующему соотношению:

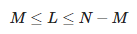
Итак, мы видим, что максимальное значение M равно ⌊N/2⌋.
Подвергая матрицу Y разложению по сингулярным числам (SVD), мы получаем:

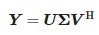
где:

• U – унитарная матрица размера (N – L) × (N – L),
• Σ — прямоугольная диагональная матрица сингулярных значений размером (N − L) × (L + 1) и
• V — унитарная матрица размера (L + 1) × (L + 1).

Если бы измеренный сигнал не содержал шума, матрица Σ содержала бы ровно M ненулевых сингулярных чисел. ценности. Из-за шума сингулярные значения могут искажаться, что проявляется в дополнительных малых сингулярных значениях. Эффект шума устраняется удалением этих малых значений. Остаются только M доминирующих значений, которые удовлетворяют следующему условию:

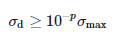
где σ_max — доминирующее единственное число, а p — количество точных значащих десятичных цифр измерения.

Затем строятся подматрицы результирующих матриц SVD:

1. Матрица U′=[u1,u2,…,u_M] размера (N − L) × M создается путем оставления столбцов, соответствующих сингулярным значениям, удовлетворяющим условию (7), и удаления остальные;
2. Квадратная диагональная матрица Σ=diag(σ1,σ2,…,σM) формируется удалением столбцов и строк матрицы Σ, содержащих сингулярные значения, не удовлетворяющие условию (7);
3. Матрица V′=[v1,v2,…,v_M] размера (L + 1) × M формируется путем оставления столбцов, соответствующих сингулярным значениям, удовлетворяющим условию (7) и удаление остальных.

Затем создается матрица V₁′ путем удаления последней строки матрицы V′. V₂′ строится путем удаления первой строки матрицы V′.

Затем рассчитываются следующие матрицы:

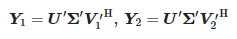
Значения zi являются ненулевыми обобщенными собственными значениями пары матриц (Y₁, Y₂), а именно собственными значениями Y ^†₁Y₂, где Y^†₁ является псевдообратным Мура-Пенроуза Y₁. Затем вычисляем полюса:

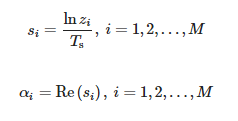
Значения амплитуд можно определить следующим образом:

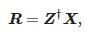
где:

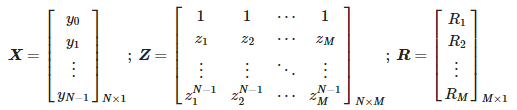
Вышеуказанные операции выполняются методом краткосрочного матричного карандаша для последовательных интервалов данных [9,22].

Приближенные результаты собственных значений, псевдоинверсий и алгоритмов SVD могут повлиять на появление zi ненулевых, хотя и близких к нулю значений. Эти значения влияют на скорость MPM и могут негативно сказаться на их результатах, поэтому их стоит удалить перед подсчетом остатков.

2.2. Поведение полюсов компонентов вблизи импульса

Неисправности в электрической сети генерируют импульсы, распространяющиеся по линиям электропередач со скоростями, близкими к скорости света [3]. Эти импульсы могут быть идентифицированы с помощью анализа сдвига полюсов приближения STMPM. На рис. 1 показаны три примера импульсов гауссовой формы и полюса их аппроксимации с помощью СТМПМ. Когда приходит импульс, аппроксимация с экспоненциальными составляющими меняется по мере перемещения временного окна. При нахождении импульса справа от средней точки окна полюсы аппроксимации имеют положительную действительную часть, при расположении вершины Гаусса в середине окна действительная часть полюсов близка к нулю, а при импульс находится в первой половине окна, полюса имеют отрицательную действительную часть. Таким образом, изменение знака действительной части полюсов указывает на то, что центр импульса прошел через среднюю точку окна выборки [9,22]. Из рисунка 2 также видно, что полюса с наибольшим абсолютным значением действительной части (и, следовательно, с наибольшей скоростью изменения амплитуды) имеют наибольшее значение начального модуля амплитуды (остатка).

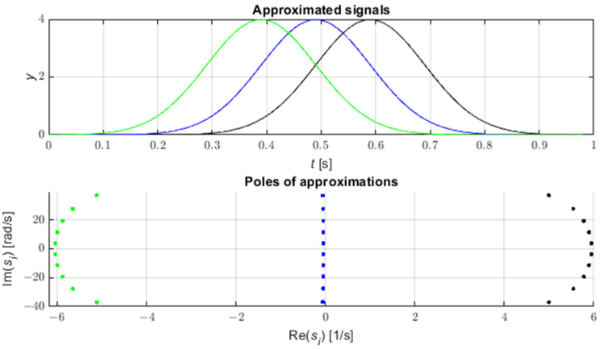
Рисунок 1. Гауссианы и соответствующие полюса аппроксимаций.

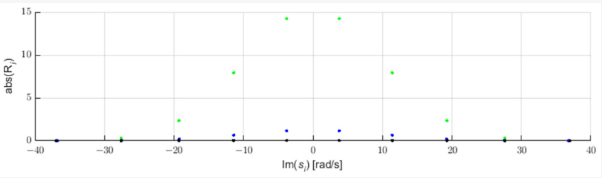
Рисунок 2. Остатки компонентов гауссовых аппроксимаций.

Итак, мы видим, что временную координату вершины импульса можно приближенно отождествить с моментом смены знака коэффициентов затухания.

Получив ход этих коэффициентов во времени с помощью СТМПМ, мы можем подвергнуть их линейной аппроксимации в окрестности точки, где коэффициенты проходят через нуль, и получить приблизительную координату вершины импульса. Следует отметить, что коэффициенты, характеризующиеся наибольшей вариабельностью, характеризуются и наибольшей амплитудой — они являются наибольшими составляющими импульса.

2.3. Алгоритм обнаружения импульсов в реальном времени

Блок-схема алгоритма обнаружения импульсов, исходящих от бегущих волн, представлена на рисунке 3. Алгоритм подвергает последовательные окна сигнала STMPM для извлечения скоростей затухания компонентов аппроксимации.

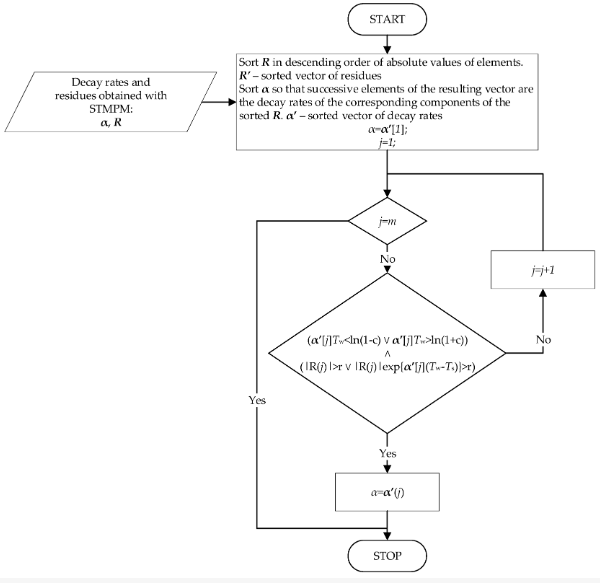
Рисунок 3. Алгоритм выбора скоростей затухания.

Полученные компоненты подвергают отбору, процедура которого представлена на рисунке 4. Отбор основан на допущении, что за пиковое время следует брать те компоненты СТМПМ, которые характеризуются наибольшей амплитудой. аппроксимации — они вносят наибольший вклад в переходную составляющую сигнала. Это согласуется с наблюдением из предыдущего пункта — компоненты с наибольшим изменением амплитуды характеризуются наибольшей начальной амплитудой. В случае, когда составляющая с наибольшей амплитудой характеризуется малой скоростью затухания в течение всего окна длиной T_w — меньше параметра c — или ее максимальный вклад в сигнал меньше r, следующая компонента по величине амплитуды выбирается как потенциальный кандидат на скорость затухания α. Повторяя эту процедуру для последующих компонентов до тех пор, пока условие не будет выполнено, в конечном итоге получают коэффициент α, который затем используется для аппроксимации времени прихода импульса. Если ни один из компонентов не удовлетворяет вышеуказанным условиям, выбирается компонент с наибольшей амплитудой.

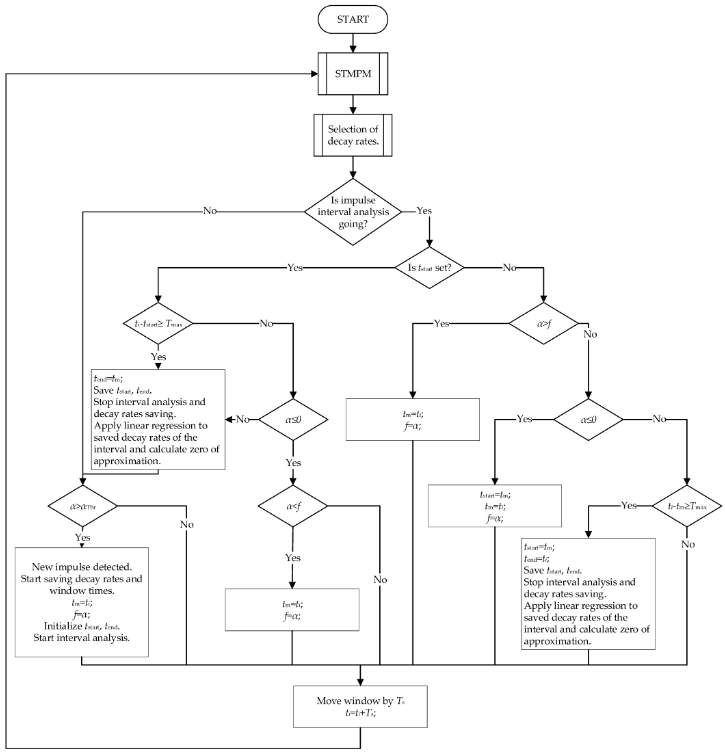
Рисунок 4. Алгоритм идентификации пульса.

Время, связанное с окном, считается:

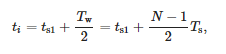
где t_s1 – время выборки первого окна, а T_w – ширина окна.

На приход импульса указывает резкое увеличение скорости α, связанное с быстрым изменением сигнала в конце окна выборки. Параметр α_Thr выбран в качестве порога скоростей затухания. При превышении порога обнаружения в память записываются последующие значения коэффициентов α и времени окна, и начинается анализ данных для определения более точных границ импульсов. Момент t_start с наибольшим значением α перед изменением знака скорости затухания выбирается как надлежащее начало импульса. Чтобы сохранить потенциальное время правильных границ импульса, была введена переменная t_m с переменной f, содержащей самые большие рассчитанные значения α импульса.

Если значение t_start найдено, начинается поиск окончательного правильного окончания импульса t_end. Это соответствует наименьшему значению α перед тем, как знак снова изменится, на этот раз на положительный. Переменная i_m снова используется для хранения предыдущих потенциальных конечных точек. Переменная f содержит предыдущие минимальные значения α.

Когда длина импульса равна T_max выборок или обнаруживается конец импульса, анализ импульса прекращается.

Функция α(t) в интервале [t_start; t_end] подвергается линейной регрессии. Коэффициенты этой регрессии находятся как решение следующей задачи:

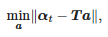
где: α_t=[α(t_начало),α(t_начало+Ts),…,α(t_конец)]^T, a=[a₁,a₀]^T

Искомые коэффициенты:

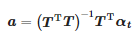
Принимая во внимание, что момент прихода импульса:

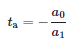
2.4. Адаптированный тестовый фидер IEEE 34-Bus

Для расчета короткого замыкания была создана тестовая модель фидера IEEE с 34 шинами в Simulink. Топология фидера показана на рис. 5 [23]. Фидер основан на реальной сети в штате Аризона. Это достаточно просто, чтобы не стать существенной вычислительной нагрузкой во время моделирования переходных процессов с небольшим шагом интегрирования. Модель была упрощена, а параметры изменены для имитации европейских сетей:

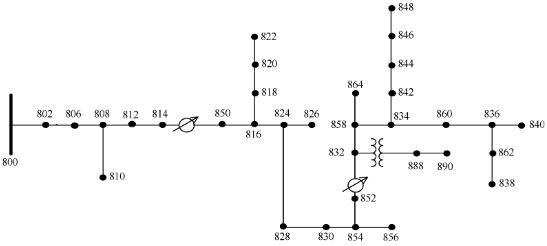
Рисунок 5. Топология фидера 34-шины IEEE.

• Напряжение сети изменено с 24,9 кВ на 16,5 кВ;
• Все участки ЛЭП принимались за воздушные с одинаковыми параметрами;
• Удалены регуляторы напряжения;
• Предполагалось, что распределенные нагрузки сосредоточены на автобусах в дальнем конце загруженных линий;
• Нагрузки были подключены к сети среднего напряжения через распределительные трансформаторы;
• Нейтраль трансформатора высокого/среднего напряжения была отключена от заземления.

Параметры источника напряжения:

• частота 50 Гц;
• Линейное напряжение 115,5 кВ;
• Сопротивление 0,00227 Ом.
• Симметричный источник со сдвигом фазы L1, равным 0°.

Параметры силового трансформатора:

• Соотношение напряжений 115,5/16,5;
• Векторная группа обмотки ВН Yg;
• Векторная группа обмотки низкого напряжения D11;
• Мощность 6,3 МВА;
• Относительное напряжение короткого замыкания 7,5%;
• Сопротивление короткому замыканию равно 0,49% эквивалентного импеданса.

Параметры распределительных трансформаторов:

• Отношение напряжения 15,75/0,4;
• Векторная группа обмотки ВН D11;
• Векторная группа обмотки низкого напряжения Yg;
• Мощность 630 кВА;
• Относительное напряжение короткого замыкания 6 %;
• Сопротивление короткому замыканию равно 17,2 % эквивалентного импеданса.

Параметры линий электропередач:

• Трехфазная линия без нейтрали;
• Один проводник на фазу;
• Диаметр проводника 0,8466 см;
• Отношение T/D 0,311;
• Сопротивление постоянному току 0,5939 Ом/км;
• Горизонтальное расположение проводников x=[−1,05, 0, 1,05];
• Вертикальное положение проводников u=[−9,05, 10,61, 9,05];
• Удельное сопротивление грунта ρ=100 Ом·м.

Каждому трансформатору были присоединены емкости, как показано на рис. 6 [5] в для моделирования свойств трансформаторов на высоких частотах.

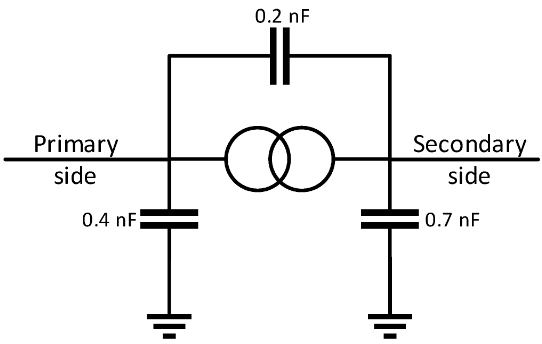
Рисунок 6. Модель трансформатора.

Линии электропередач были смоделированы в диапазоне от 1 Гц до 1 МГц с учетом скин-эффекта с использованием универсальной модели линии.

Моделирование однофазных и многофазных коротких замыканий с переходным сопротивлением через нуль проводилось при 20%, 50%, 80% и 100% длине линий. Это соответствует 76 местам короткого замыкания. Шаг интегрирования моделирования составлял Δt=0,1 мкс. Использовался метод интегрирования Тастина/обратного Эйлера.

3. Результаты

3.1. Измерения характеристик передачи датчика среднего напряжения

Измерения АЧХ проводились для датчика среднего напряжения, предназначенного для монтажа в соединительных головках. Датчик представлял собой резистивный делитель с номинальным первичным напряжением 20/√3 кВ и номинальным вторичным напряжением 3,25/√3, что соответствует соотношению напряжений:

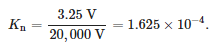
Для измерений использовался векторный анализатор цепей Bode 100 компании OMICRON Lab. Это устройство позволяет проводить измерения в диапазоне от 1 Гц до 50 МГц. Для проведения испытаний использовалась функция измерения усиления и фазы устройства. Эта функция была основана на сравнении амплитуды и фазы сигналов напряжения на первичной и вторичной сторонах датчика. Измерение передаточной функции, определяемой как отношение напряжения на вторичной стороне к напряжению на первичной стороне, выполнялось для 2048 значений частоты в диапазоне от 10 Гц до 20 МГц. Измеренные значения представлены на рисунке 7.

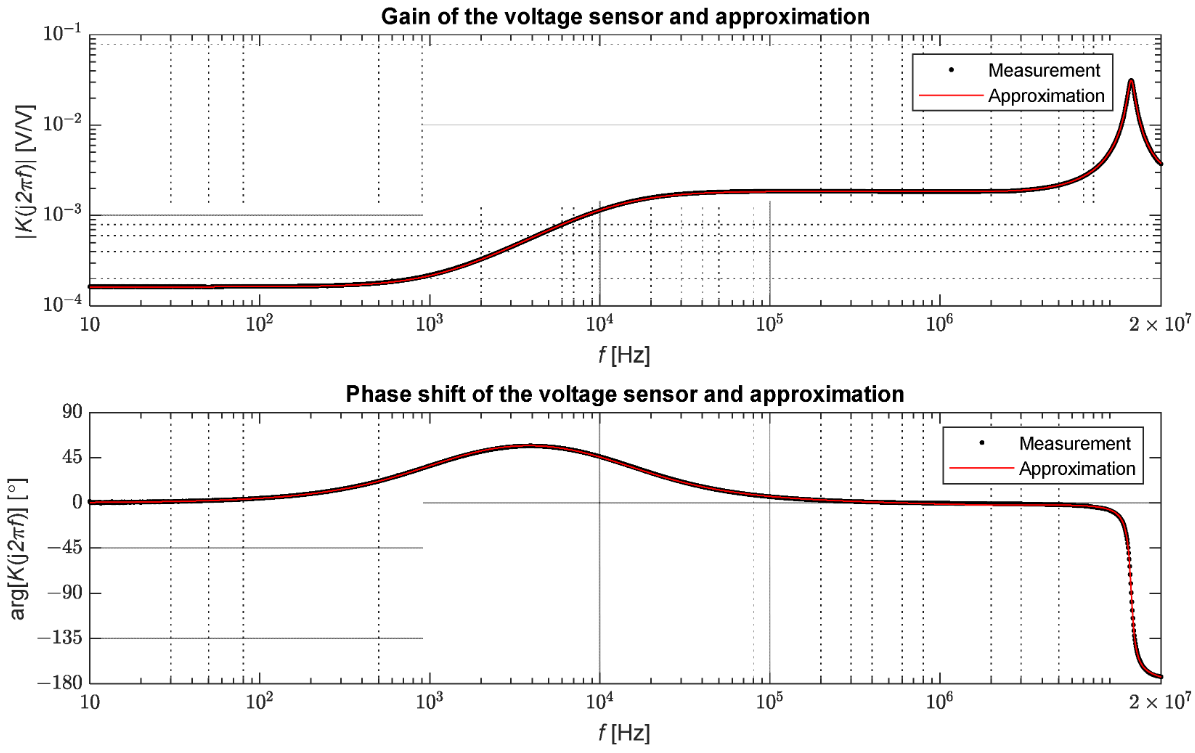
Рисунок 7. Результаты измерения коэффициента пропускания датчика среднего напряжения.

Испытуемый датчик напряжения сохраняет номинальный коэффициент передачи для сигналов до частоты около 1 кГц, затем график поднимается до уровня усиления около 1,84×10⁻³; этот уровень поддерживается в пределах примерно от 12,5 кГц до 6,6 МГц. Благодаря дифференцирующему свойству датчика здесь наблюдается положительный фазовый сдвиг примерно 57° в переходной зоне от 100 Гц к 100 кГц. В случае фазы можно выделить две зоны, для которых смещение не превышает 6°. При этом диапазон частот составляет примерно до 130 Гц и от 105 кГц до 9,4 МГц. Следовательно, можно сделать вывод, что в диапазоне от 105 кГц до 6,6 МГц сигналы пропорционально преобразуются, но с другим коэффициентом пропорциональности, чем вблизи частоты сети. В случае волновых явлений этого диапазона достаточно, чтобы точно представить форму волн, распространяющихся по сетке [20]. Стоит отметить, что датчики напряжения разной конструкции могут иметь разные передаточные свойства.

Для разработки математической модели датчика использовалась функция tfest пакета MATLAB для аппроксимации полученных данных устойчивой передаточной функцией следующего вида:

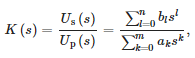
где:

• Up(s) — напряжение на первичной стороне датчика,
• Us(s) — напряжение на вторичной обмотке датчика,
• n — порядок числителя,
• m — порядок знаменателя и
• ak, bl — коэффициенты полиномов от знаменателя и числителя коэффициента пропускания последовательно.

Значения коэффициентов передаточной функции представлены в таблице 1. Стоит отметить, что смоделированный коэффициент пропускания является правильным, поскольку порядок знаменателя выше порядка числителя. На рис. 7 также представлено сравнение передаточных функций, полученных из измерений с аппроксимацией по формуле (19). Также рассчитывалась среднеквадратическая ошибка между точками измерения и аппроксимацией, определяемая следующим соотношением:

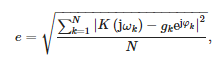
где:

• N = 2048 — количество частот измерений.
• g_k — измеренный коэффициент усиления датчика при пульсации ω_k и
• φ_k — измеренный фазовый сдвиг датчика при пульсации ω_k.

Значение ошибки аппроксимации равно:

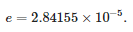
Таблица 1. Значения полиномиальных коэффициентов эквивалентного пропускания датчика напряжения с резистивной делительной структурой.

На рис. 8 показано сравнение формы сигнала фазного напряжения на подстанции, полученной в результате моделирования, и напряжения на выходе смоделированного датчика в случае прямого трехфазного короткого замыкания на землю в узле 816. хорошо видно, что усиление быстрых переходных процессов больше, чем медленных переходных процессов. Стоит отметить, что эти сигналы усиливаются почти пропорционально.

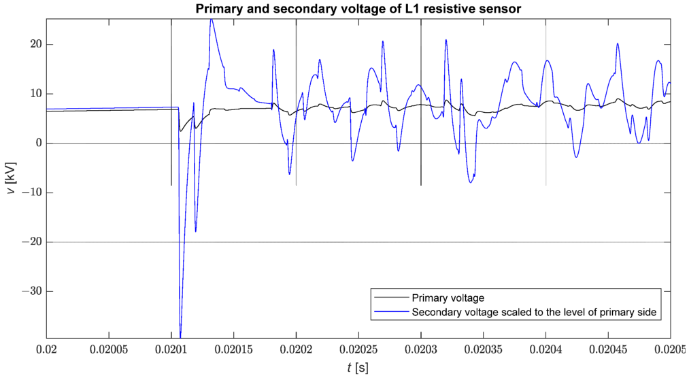
Рис. 8. Сравнение осциллограммы фазного напряжения (v_L1) и напряжения на выходе датчика, приведенного к первичному напряжению (v_L1/K_n) во время ошибки.

3.2. Идентификация импульсов короткого замыкания с использованием STMPM

Рисунок 9 показывает форму волны всех скоростей затухания примерной формы волны напряжения на подстанции после трехфазного короткого замыкания с нулевым импедансом на землю в узле 816 модели. Можно видеть, что отсутствие выбора скоростей затухания затрудняет локализацию импульсов; это особенно верно для более слабых импульсов. С другой стороны, визуальное наблюдение скорости затухания позволяет легко идентифицировать интервалы, содержащие импульсы, в случае визуального анализа форм сигналов фазного напряжения, хотя это не всегда легко в случае малых амплитуд импульсов.

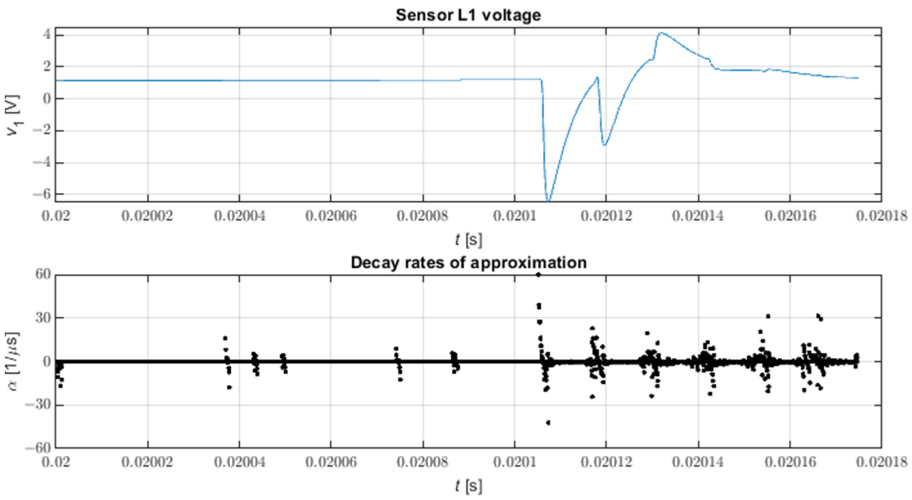
Рисунок 9. Все скорости затухания приближения STMPM. N = 9, L = 4.

На рис. 10 показаны выбранные скорости затухания вместе с линейной регрессией, используемой для определения момента прихода импульса. Количество ложных срабатываний можно уменьшить, отфильтровав ненужные коэффициенты затухания.

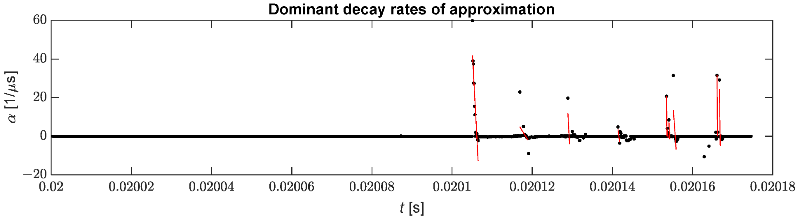
Рисунок 10. Выбранные скорости затухания, используемые для идентификации импульсов.

В табл. 2 приведены ошибки определения времени прихода первой приходящей волны на станцию. Эта ошибка определяется следующим уравнением:

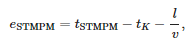
где:

• t_STMPM — момент прибытия согласно STMPM,
• t_K — момент неисправности,
• l — расстояние места КЗ от подстанции и
• v = 299 552 300 м/с — скорость распространения волн разлома, измеренная для короткого замыкания в самом дальнем узле (838).

Параметры метода, используемые для получения результатов:

• N = 5 — количество выборок за временное окно;
• L = 2 — параметр карандаша;
• p = 6 — количество точных значащих десятичных цифр измерения;
• α_Thr=1051s — порог обнаружения импульса;
• T_max=2,1 мкс — максимальная длительность импульса;
• T_w=0,5 мкс — ширина окна;
• T_s=0,1 мкс — период выборки;
• r=0,02 В — порог амплитуды.

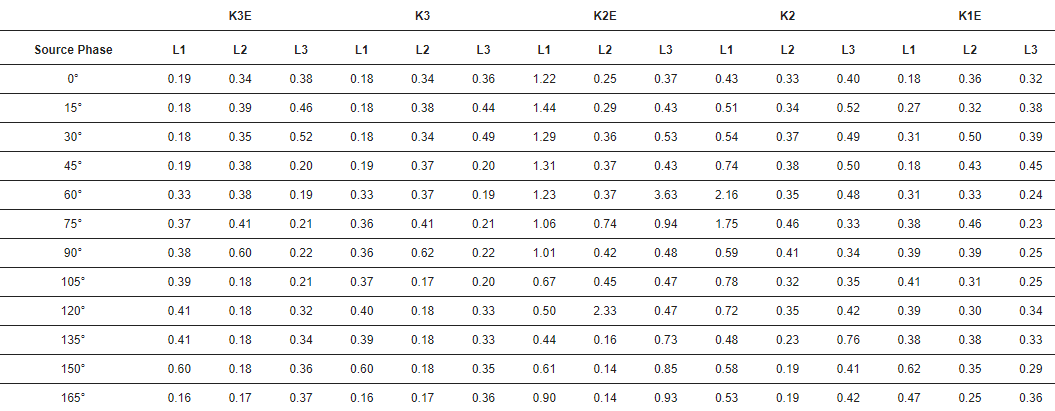
В таблице 3 показаны стандартные отклонения временной ошибки пульса.

Таблица 2. Временная ошибка идентификации волн при различных разломах. Единица: мкс. K3E—трехфазное замыкание на землю, K3—трехфазное замыкание, K2E—двухфазное замыкание на землю, K2—двухфазное замыкание, K1E—фаза-короткое замыкание на землю.

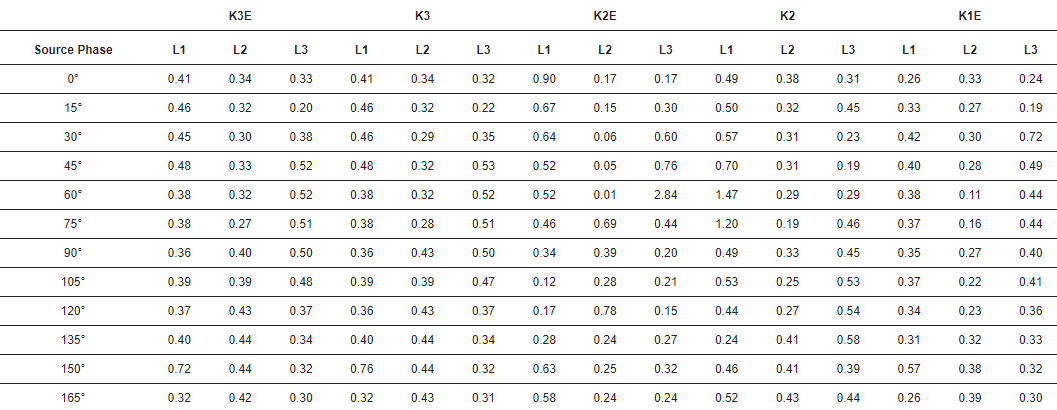
Таблица 3. Стандартное отклонение временной ошибки. Единица: мкс. K3E—трехфазное замыкание на землю, K3—трехфазное замыкание, K2E—двухфазное замыкание на землю, K2—двухфазное замыкание, K1E—фаза-короткое замыкание на землю.

4. Обсуждение

Разработана модель передаточной функции резистивного датчика напряжения на основе широкополосных измерений от 10 Гц до 20 МГц. Моделирование бегущих волн, генерируемых неисправностью, в модели 34-шины IEEE выполнялось с использованием передаточной функции. Частотная характеристика резистивного датчика была достаточной для идентификации волн неисправности в сигнале вторичного напряжения. Датчик преобразует сигналы бегущей волны с приблизительно постоянным усилением, которое больше, чем усиление на частоте сети. Для идентификации использовался новый алгоритм реального времени, основанный на методе матричного карандаша. Вариант этого метода, использованный в статье, характеризуется высокой точностью идентификации волн, так как средняя ошибка составила 0,41 мкс при частоте дискретизации 10 МГц, причем ошибка имела положительное значение, поэтому найденное время прихода было больше реального. Однако следует отметить, что при практических применениях метода, например, при волновой локализации разломов, часть этой погрешности устраняется за счет дифференциальной работы этих алгоритмов. Точная идентификация волн неисправностей может позволить классифицировать и локализовать неисправности в сетях среднего напряжения, используя сборные шины в качестве единственной точки измерения. Тест с использованием реальных сигналов необходим для проверки эффективности алгоритма и сравнения его с другими методами идентификации входящих волновых импульсов. Вполне корректное преобразование напряжения датчиками может позволить классифицировать тип неисправности по амплитудам генерируемых ими волн.

использованная литература

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Автор статьи: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).