Морате бити пријављени да
Идентификација путујућих таласа у сигналу напонског сензора у мрежи средњег напона коришћењем методе краткотрајне матрице оловке

Идентификација путујућих таласа у сигналу напонског сензора у мрежи средњег напона коришћењем методе краткотрајне матрице оловке
У тестовима је коришћен Омицрон-Лаб Боде 100 векторски анализатор кола ДАЦПОЛ СП. ЗОЛОШКИ ВРТ.
Сажетак
Већина метода локализације таласа квара заснована је на анализи линијске струје трансформисане струјним трансформаторима и ограничена је на мреже високог напона. Локализација таласа квара у средњенапонским мрежама се још увек развија. Овај рад представља нови алгоритам у реалном времену за идентификацију путујућих таласа у дистрибутивној мрежи коришћењем напонског сигнала и методе краткотрајне матричне оловке. За добијање таласних облика секундарног бочног напона на трафостаници развијен је модел отпорног сензора напона заснованог на широкопојасним мерењима од 10 Хз до 20 МХз. Тестирани сензор појачава фреквенције повезане са путујућим таласима више од фреквенције корисности што омогућава идентификацију. Симулације кратког споја на ИЕЕЕ 34-бус фидеру су извршене да би се тестирао алгоритам. Развијена метода може детектовати чак и таласе мале амплитуде.
1. Увод
Заштита електроенергетског система од кварова је један од циљева заштитног релеја. Брзо отклањање сметњи ограничава штету нанесену електроенергетској опреми и смањује њен негативан утицај на квалитет електричне енергије. Стога је развој брзих и тачних релеја и локатора кварова у дистрибутивним мрежама кључно питање и са техничког и са економског становишта. У случају високонапонских мрежа, локализација кварова је лака јер их карактерише велика дисперзија мерења и структура петље. У случају дистрибутивних мрежа мерења се углавном врше на једној тачки тамошње трафостанице. Штавише, дистрибутивне мреже су структуре стабла, што чини идентификацију покварених грана неизвесном. Решење овог проблема може бити употреба локатора путујућих таласа, који у овом случају могу бити прецизнији од конвенционалних метода. Да би употреба оваквих локатора била могућа, неопходно је развити најтачније методе идентификације путујућих таласа.
Конвенционални приступ откривању квара заснован је на анализи струја и напона основне фреквенције. Из тог разлога, заштитни алгоритми засновани на овим типовима сигнала захтевају анализу интервала сигнала који је довољно дугачак да се увери да је дошло до поремећаја. Модернији приступ заснива се на путујућим таласима, који су сигнали више фреквенције који се шире дуж далековода. Ова врста заштите се понекад назива „ултра-висока брзина“. Он детектује струјне и напонске таласе настале услед кварова. Затим, ова заштита одређује и врсту и локацију сметње на основу поређења њихових амплитуда и времена доласка на мерне уређаје. Без сумње, кључна предност заштите засноване на таласима је брзина рада (мање од 4 мс) [1]. Штавише, ради исправно са далеководима са серијском компензацијом и током промена снаге.
Локација квара помоћу путујућих таласа може се поделити на шеме са два терминала и са једним терминалом. У случају двоструких терминалних релеја, аквизиција мерних података се дешава на крајевима заштићених водова и захтева пренос мерних података између уређаја. Међутим, релеји са једним терминалом анализирају сигнале струја и напона само са једне мерне тачке. Потребно је нагласити да се релеји са два терминала одликују већом поузданошћу јер користе таласе директно генерисане сметњом да би је локализовали и класификовали. Ови таласи имају највећу могућу амплитуду и детектују се први након квара. Међутим, у случају релеја са једним терминалом, заштита се заснива на таласу генерисаном сметњом и на таласима који се одбијају од дисконтинуитета линија, грана и самог квара [2]. То је због недостатка друге тачке мерења у мрежи.
Високонапонске мреже карактерише присуство трафостаница са мерном опремом на крајевима водова. Због тога се овде користе двополни релеји. У случају дистрибутивних мрежа, високо/средњенапонске трафостанице су обично једино место где: се постављају заштитни релеји са трансформаторима или сензорима. То значи да је у дистрибутивним мрежама коришћење једноструких таласних релеја најјефтиније решење.
Дистрибуционе мреже су мреже са топологијом стабла, а ова карактеристика отежава тачну локацију квара. И за конвенционалне и за таласне локаторе кварова ситуација је компликованија него у преносним мрежама, пошто неколико потенцијално оштећених грана може постојати на познатој удаљености од трафостанице. Само једна од грана је оштећена. Међутим, краткоспојна линија се може одредити упоређивањем амплитуда струјних таласа расутих на сабирницама подстанице [2,3,4].
Предложене су различите методе лоцирања кварова, као што је детекција фреквенција повезаних са осцилацијама таласа између чворова [5], поређење измерене струје са предвиђеном за дату локацију кратког споја [6] и традиционалније методе засноване на детекцији таласних фронтова раседа [3,7]. Следеће методе су коришћене за детекцију таласних фронтова: таласна трансформација, анализа главних компоненти заснована на екстракцији обележја, Тигеров енергетски оператор, ансамбл емпиријска декомпозиција модова и метода матричне оловке која се разматра и користи у овом раду [8,9]. Метода матричне оловке се користи за разлагање сигнала у збир експоненцијално пригушених синусоида [10]. У области електроенергетике, метода матричне оловке је коришћена за процену основних модова осцилација услед кварова и за процену хармоника и субхармоника [11,12,13].
Електрични сигнали обрађени алгоритмима дигиталне обраде података допремају се до релеја помоћу мерних уређаја који се налазе на станици. Ови уређаји укључују струјне и напонске трансформаторе, Роговски калемове или сензоре који смањују ниво електричних сигнала на ниво прихватљив за релеје. Важно је да се сигнал на секундарној страни ових уређаја репродукује што је прецизније могуће и идеално би требало да буде само скалиран. У пракси, међутим, мерни инструменти имају променљиво појачање и фазни помак у зависности од фреквенције сигнала. Високе фреквенције не би требало да буду пригушене инструментом превише да би се могао детектовати долазећи путујући талас, који је таласни облик који се брзо мења и стога садржи компоненте високе фреквенције. Потребно је нагласити да, како би се тачно репродуковала амплитуда таласа квара, инструмент треба да уведе константно временско кашњење (по могућности да га уопште нема) и да његове карактеристике појачања треба да буду што мање променљиве.
Трансформатори су инструменти који се традиционално користе у електроенергетској индустрији за мерење напона. Одликује их врло прецизна трансформација електричних сигнала, али имају и недостатке. Они доприносе негативном феномену ферорезонанце, изложени су оштећењима изазваним кратким спојевима у секундарном колу и нису у стању да прецизно трансформишу високофреквентне (>3 кХз) компоненте напона [14]. Због тога су развијени неконвенционални сензори засновани на механизмима другачијим од система трансформатора као одговор на потребу прецизног мерења прелазних компоненти. [15,16].
За мерења напона, напонски сензори засновани на капацитивним (Ц), отпорним (Р) и отпорно-капацитивним (РЦ) делиоцима су популарни неконвенционални сензори [14]. Конкретно, Р и РЦ разделници су најпопуларнији јер нису у стању да индукују ферорезонанцију због занемарљиве индуктивности, прецизно трансформишу транзијенте и високе фреквенције, омогућавајући пражњење акумулираног наелектрисања на линији и отпорни су на кратке спојеве на секундарној страни. Ови делиоци се могу успешно користити за мерење квалитета електричне енергије и за лоцирање кратког споја коришћењем таласних феномена.
Литература о моделирању конвенционалних трансформатора је огромна, али се, нажалост, обично односи на опис њихових карактеристика на фреквенцијама испод 10 кХз. [15,17]. Штавише, аутори нису успели да пронађу нумеричке податке Бодеових дијаграма или преносних функција напонских трансформатора (и конвенционалних и неконвенционалних) до 1 МХз чак ни у чланцима који описују студије у овој области. [18,19]. Такви подаци су доступни за конвенционални струјни трансформатор [20]. Наравно, сензори се разликују по дизајну, што доводи до варијација њихових карактеристика преноса од једног типа до другог, али познавање функције преноса примера изгледа да је потребно.
Да би се добили такви подаци, извршена су мерења фреквенцијских карактеристика сензора средњег напона. Затим су коришћени за развој његовог модела преносне функције. Затим је представљена побољшана метода краткотрајне матричне оловке у примени на детекцију таласа кратког споја напона у средњонапонској мрежи мерених на секундарној страни напонских сензора.
Структура рада је следећа. Одељак 2 даје опис кратковремене матричне оловке са њеном применом за проналажење сигналних импулса. Такође је обезбеђен алгоритам за идентификацију импулса. Одељак 3 садржи резултате мерења преносне функције сензора напона и резултате рада алгоритма на основу спроведених симулација. Закључци су дати у одељку 4.
2. Идентификација импулса квара у мрежи средњег напона
2.1. Метода краткотрајне матрице оловке
Метода оловке матрице кратког времена (СТМПМ) апроксимира сигнал унутар прозора који се креће током времена као збир синусоидних компоненти са експоненцијално променљивом амплитудом [10,21]:
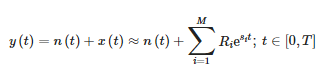
где:
- y(t)—мерни сигнал,
- n(t)—шум,
- x(t)—оригинални сигнал,
- Ri—остатак или комплексне амплитуде компоненти,
- Si—комплексни полови и
- M—број компоненти апроксимације.
За узорковани сигнал t = kTs, горња једначина има следећи облик:
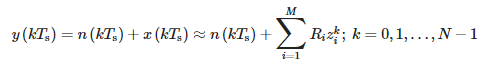
где:
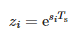
- Ts—период узорковања и
- N—број узорака.
Да би се одредили параметри апроксимације, конструише се следећа матрица:

Ево, L је параметар оловке. Број компоненти апроксимације M задовољава следећу релацију:
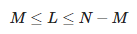
Дакле, видимо да је максимална вредност M једнака ⌊N/2⌋.
Подвргавањем матрице Y декомпозицији сингуларних вредности (СВД) добијамо:
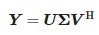
где:
- U—унитарна матрица величине (N − L) × (N − L),
- Σ—правоугаона дијагонална матрица сингуларних вредности величине (N − L) × (L + 1) and
- V—унитарна матрица величине (L + 1) × (L + 1) size.
Ако измерени сигнал не садржи шум Σ матрица би садржала тачно M једнину која није нула вредности. Услед буке сингуларне вредности могу бити изобличене, што се манифестује додатним малим сингуларним вредностима. Ефекат буке се елиминише уклањањем ових малих вредности. Остале су само M доминантне вредности које задовољавају следећи услов:
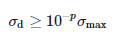
где је σmax доминантна сингуларна вредност, а п је број тачних значајних децималних цифара мерења.
Онда се конструишу подматрице резултујућих СВД матрица:
- Матрица U′=[u1,u2,…,uM] величине (N − L) × M се креира остављањем колона које одговарају сингуларним вредностима које задовољавају услов (7) и уклањањем остали,
- Квадратна дијагонална матрица Σ=диаг(σ1,σ2,…,σМ) се формира уклањањем колона и редова матрице Σ, који садрже сингуларне вредности које не задовољавају услов (7);
- Матрица V′=[v1,v2,…,vM] величине (L + 1) × M се формира остављањем колона које одговарају сингуларним вредностима које задовољавају услов (7) и уклањајући остале.
Онда се матрица V1′ креира уклањањем последњег реда матрице V′. V2′ се гради уклањањем првог реда V′ матрице.
Затим се израчунавају следеће матрице:
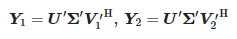
Вредности зи су ненулте генерализоване сопствене вредности пара матрица (Y1, Y2), наиме сопствене вредности од Y†1Y2, где Y†1 је Мооре–Пенросе псеудоинверзан од Y1. Затим израчунавамо стубове:
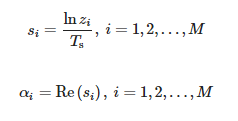
Вредности амплитуда се могу одредити на следећи начин:
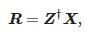
где:
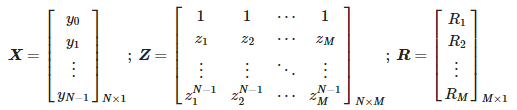
Горе наведене операције се изводе у методи оловке матрице кратког времена за узастопне интервале података [9,22].
Приближни резултати сопствених вредности, псеудоинверзија и СВД алгоритама могу утицати на појаву зи који није нула, иако је близу нулте вредности. Ове вредности утичу на брзину МПМ и могу негативно утицати на њихове резултате, тако да је вредно да их уклоните пре израчунавања остатака.
2.2. Понашање компонентних полова у близини пулса
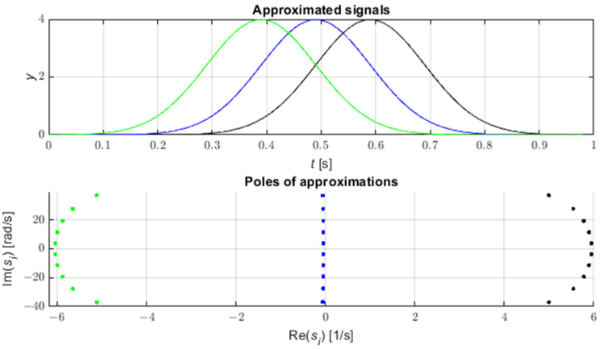
Грешке у електричној мрежи стварају импулсе који се шире дуж далековода брзинама близу брзине светлости [3]. Ови импулси се могу идентификовати коришћењем анализе померања полова СТМПМ апроксимације. На слици 1 приказана су три примера импулса Гаусовог облика и полови њихове апроксимације са СТМПМ. Када дође импулс, апроксимација са експоненцијалним компонентама се мења како се временски прозор помера. Када је пулс десно од средње тачке прозора, полови апроксимације имају позитиван реални део, када је Гаусов врх у средини прозора реални део полова је близу нуле, а када је пулс је у првој половини прозора полови имају негативан реални део. Промена предзнака правог дела полова стога указује да је центар импулса прошао кроз средњу тачку прозора за узорковање [9,22]. Такође са слике 2 можемо видети да полови са највећом апсолутном вредношћу реалног дела (а самим тим и са најбржом брзином промене амплитуде) имају највећу вредност почетног амплитудног модула (резидуума).
Слика 1. Гаусови и одговарајући полови апроксимација.
Слика 2. Остаци компоненти Гаусових апроксимација.
Дакле, видимо да се временска координата врха импулса може приближно поистоветити са тренутком промене предзнака коефицијената пригушења.
Добијајући временски зависни ток ових коефицијената уз употребу СТМПМ, можемо их подвргнути линеарној апроксимацији у близини тачке где коефицијенти пролазе кроз нулу и добити приближну координату врха импулса. Треба напоменути да се коефицијенти које карактерише највећа варијабилност карактерише и највећа амплитуда — они су највеће компоненте пулса.
2.3. Алгоритам за детекцију пулса у реалном времену
Дијаграм тока алгоритма за детекцију импулса који потичу од путујућих таласа представљен је на слици 3. Алгоритам подвргава узастопне прозоре сигнала СТМПМ-у како би извукао стопе опадања компоненти апроксимације.
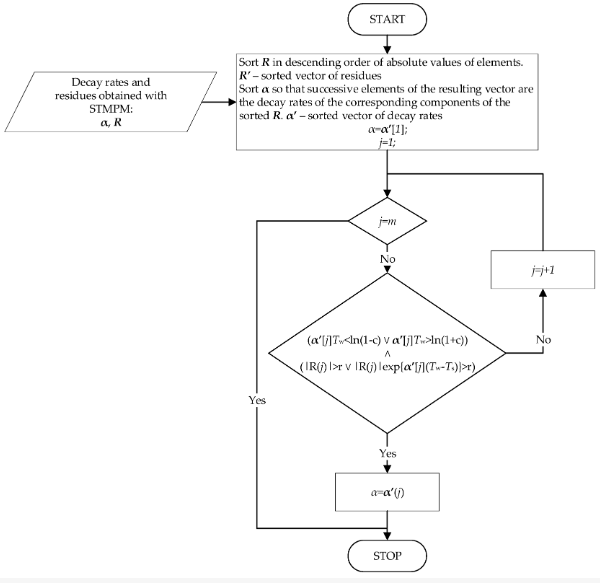
Слика 3. Алгоритам избора брзина распада.
Добијене компоненте се подвргавају селекцији, чији је поступак приказан на слици 4. Селекција је заснована на претпоставци да за време вршног удара треба узети оне компоненте СТМПМ које се одликују највећом амплитудом. апроксимација—они представљају највећи допринос прелазној компоненти сигнала. Ово је у сагласности са запажањем из претходне тачке—компоненте са највећом варијацијом амплитуде карактерише највећа почетна амплитуда. У случају када компоненту са највећом амплитудом карактерише мала брзина распада током целог прозора дужине Tw—Добијене компоненте се подвргавају селекцији, чији је поступак приказан на слици 4. Селекција је заснована на претпоставци да за време вршног удара треба узети оне компоненте СТМПМ које се одликују највећом амплитудом. апроксимација—они представљају највећи допринос прелазној компоненти сигнала. Ово је у сагласности са запажањем из претходне тачке—компоненте са највећом варијацијом амплитуде карактерише највећа почетна амплитуда. У случају када компоненту са највећом амплитудом карактерише мала брзина распада током целог прозора дужине.
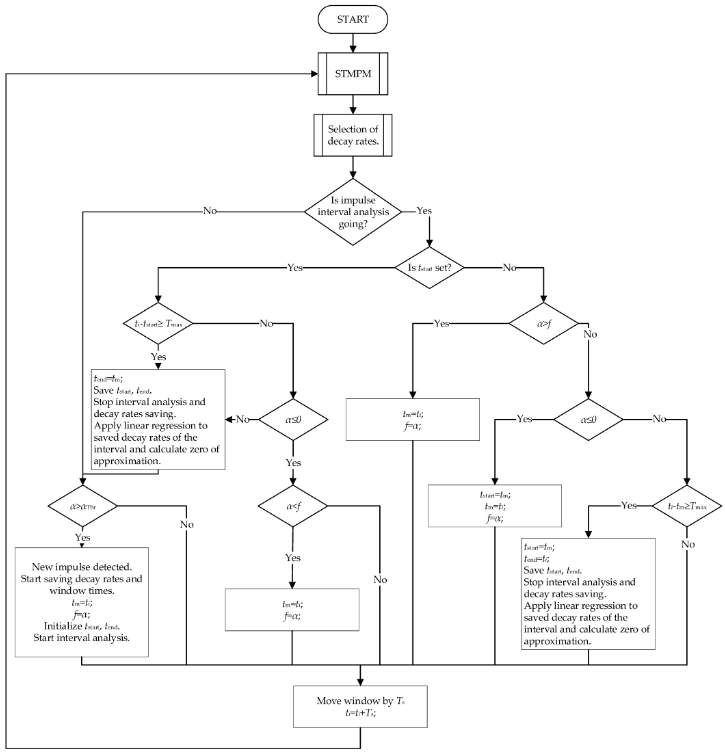
Слика 4. Алгоритам идентификације импулса.
Сматра се да је време повезано са прозором:
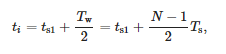
where ts1—време првог узорка прозора и Tw—ширина прозора.
Долазак импулса је означен наглим повећањем α брзина повезаних са брзом променом сигнала на крају прозора узорковања. Параметар αThr је изабран као праг стопа распадања. Када се прекорачи праг детекције, следеће вредности α коефицијената и времена прозора се уписују у меморију, а анализа података почиње да би се одредиле прецизније границе импулса. Тренутак tstart са највећом вредношћу α пре промене предзнака брзине распада се бира као правилан почетак импулса. Да би се сачувала потенцијална времена тачних граница импулса, променљива tm је уведен са променљивом f који садржи највеће вредности α пулса израчунате до сада.
Ако вредност од tstart је пронађен, тражење коначног правилног краја пулса tend почиње. Ово одговара најмањој вредности α пре него што се предзнак поново промени, овог пута у позитиван. Променљива im се поново користи за чување претходних потенцијалних крајњих тачака. Променљива f садржи претходне минималне вредности α.
Када је дужина импулса једнака Tmax узорака или се пронађе крај импулса, анализа импулса се завршава.
Функција α(т) у интервалу [tstart; tend] је подвргнут линеарној регресији. Коефицијенти ове регресије налазе се као решење следећег проблема:
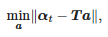
где: αt=[α(tstart),α(tstart+Ts),…,α(tend)]T, a=[a1,a0]T

Тражени коефицијенти су:
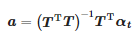
Док је тренутак доласка импулса:
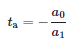
2.4. Прилагођени ИЕЕЕ 34-бус тест фидер
За прорачуне кратког споја, креиран је ИЕЕЕ тест фидер модел са 34 магистрале у Симулинк-у. Топологија фидера је приказана на слици 5 [23]. Фидер је заснован на правој мрежи у држави Аризона. Довољно је једноставно да не постане значајно рачунарско оптерећење током симулација прелазних процеса са малим кораком интеграције. Модел је поједностављен, а параметри су промењени да би имитирали европске мреже:
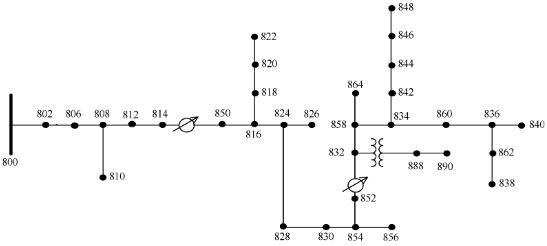
Слика 5. Топологија ИЕЕЕ 34-сабирнице.
- Напон мреже је промењен са 24,9 кВ на 16,5 кВ;
- Претпостављало се да су сви делови далековода надземни са истим параметрима;
- Регулатори напона су уклоњени;
- Претпостављало се да је распоређено оптерећење скупљено у аутобусима на крајњем крају оптерећених линија;
- Терети су прикључени на средњенапонску мрежу преко дистрибутивних трансформатора;
- Неутрална тачка трансформатора високог/средњег напона је искључена са уземљења.
Параметри извора напона:
- 50 Хз фреквенција;
- мрежни напон 115,5 кВ;
- Отпор 0,00227 Ω.
- Симетричан извор са фазним померањем фазе Л1 једнаким 0°.
Параметри енергетског трансформатора:
- Однос напона 115,5/16,5;
- Векторска група високонапонских намотаја Иг;
- Векторска група нисконапонских намотаја Д11;
- Снага 6,3 МВА;
- Релативни напон кратког споја 7,5%;
- Отпор кратког споја једнак 0,49% еквивалентне импедансе.
Параметри разводних трансформатора:
- Однос напона 15,75/0,4;
- Векторска група високонапонских намотаја Д11;
- Векторска група нисконапонских намотаја Иг;
- Снага 630 кВА;
- Релативни напон кратког споја 6%;
- Отпор кратког споја једнак 17,2% еквивалентне импедансе.
Параметри електричних водова:
- Трофазни вод без нуле;
- Један проводник по фази;
- Пречник проводника 0.8466 cm;
- Т/Д однос 0,311;
- Отпор једносмерне струје 0,5939 Ω/км;
- Хоризонтални положај проводника x=[−1.05, 0, 1.05];
- Вертикални положаји проводника u=[−9.05, 10.61, 9.05];
- Отпор уземљења ρ=100 Ωm.
Капацитивности су прикључене на сваки трансформатор као што је приказано на слици 6 [5] у циљу моделирања особина трансформатора на високим фреквенцијама.
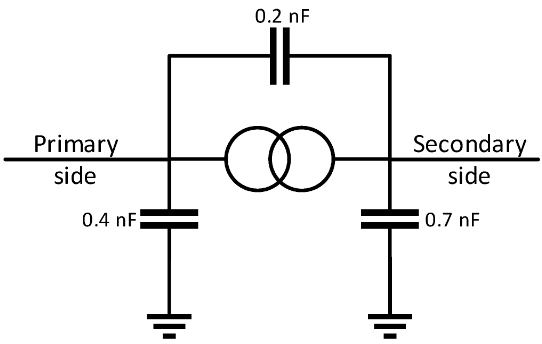
Слика 6. Модел трансформатора.
Напонски водови су моделовани између 1 Хз и 1 МХз узимајући у обзир скин ефекат коришћењем Универсал Лине Модела.
Симулације једнофазних и вишефазних кратких спојева са отпором укрштања нуле изведене су на 20%, 50%, 80% и 100% дужине водова. Одговара 76 локација кратког споја. Корак интеграције симулације био је Δt=0.1 μs. Тустин/Бацквард Еулер је био коришћен метод интеграције.
3. Резултати
3.1. Мерење карактеристика преноса сензора средњег напона
Мерења фреквентног одзива су извршена за средњенапонски сензор намењен за уградњу у конекторске главе. Сензор је био отпорни делилац са номиналним примарним напоном од 20/√3 kV и номиналним секундарним напоном од 3.25/√3, што одговара односу напона од:
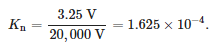
За мерења је коришћен векторски анализатор мреже ОМИЦРОН Лаб Боде 100. Овај уређај омогућава мерења у опсегу од 1 Хз до 50 МХз. За извођење тестова коришћена је функција мерења појачања и фазе уређаја. Ова функција је заснована на поређењу амплитуде и фазе напонских сигнала на примарној и секундарној страни сензора. Мерење функције преноса, дефинисано као однос напона на секундарној страни и напона на примарној страни, изведено је за 2048 вредности фреквенције у опсегу од 10 Хз до 20 МХз. Измерене вредности су приказане на слици 7.
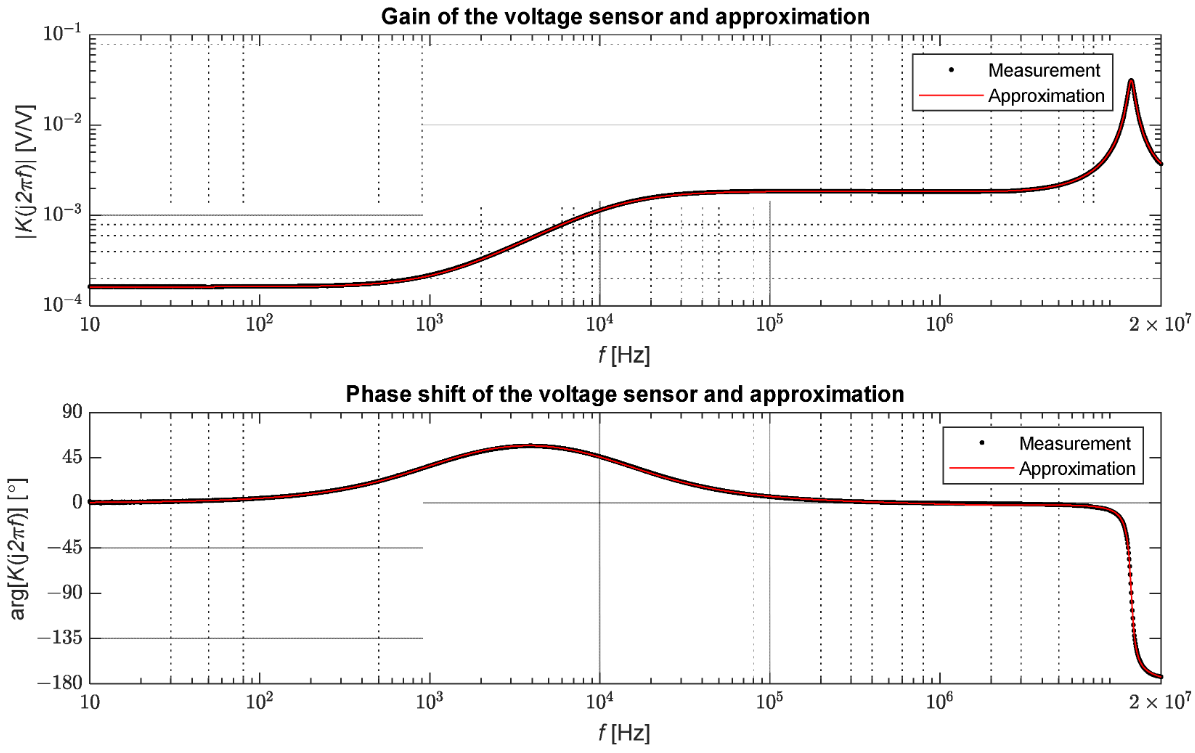
Слика 7. Резултати мерења пропусности средњенапонског сензора.
Тестирани сензор напона одржава номинални коефицијент преноса за сигнале до фреквенције од око 1 кХз, а затим се дијаграм подиже до нивоа појачања од око 1.84 ×10−3; овај ниво се одржава између око 12,5 кХз до 6,6 МХз. Због диференцирајућег својства сензора, овде је позитиван фазни помак од приближно 57° у прелазној зони од 100 Хз до 100 кХз. У случају фазе можемо разликовати две зоне за које помак не прелази 6°. У овом случају, опсег фреквенција је до приближно 130 Хз и од 105 кХз до 9,4 МХз. Дакле, може се закључити да се у опсегу од 105 кХз до 6,6 МХз сигнали пропорционално трансформишу али са другачијим фактором пропорционалности него близу фреквенције мреже. У случају таласних феномена, овај опсег је довољан да тачно представи облик таласа који се шире у мрежи. [20]. Вреди напоменути да напонски сензори са различитим конструкцијама могу показати различите карактеристике преноса.
Да би се развио математички модел сензора, МАТЛАБ-ова функција „тфест“ је коришћена за апроксимацију података добијених стабилном функцијом преноса следећег облика:
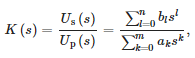
где:
- Up(s) — напон на примарној страни сензора,
- Us(s) — напон на секундарној страни сензора,
- n — ред бројилаца,
- m — ред имениоца и
- ak, bl — коефицијенти полинома имениоца и бројила пропусности, сукцесивно.
Вредности коефицијената функције преноса су представљене у табели 1. Вреди напоменути да је моделирана пропусност исправна јер је ред имениоца већи од реда бројилаца. На слици 7 је такође приказано поређење преносних функција добијених мерењима са апроксимацијом Формулом (19). Израчуната је и средња квадратна грешка између тачака мерења и апроксимације одређене следећом релацијом:
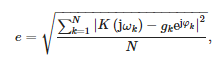
где:
- N = 2048—број мерних фреквенција
- gk —измерено појачање сензора при пулсирању ωk and
- φk —измерени фазни помак сензора при пулсирању ωk.
Вредност грешке апроксимације је једнака:
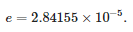
Табела 1. Вредности полиномских коефицијената еквивалентне пропусности напонског сензора са отпорном структуром делиоца.

На слици 8 приказано је поређење таласног облика фазног напона на трафостаници добијеног из симулације и напона на излазу моделованог сензора у случају директног трофазног кратког споја са земљом на чвору 816. Јасно је видљиво да појачање брзих прелазних појава је веће од спорих транзијента. Вреди напоменути да се ови таласни облици појачавају скоро пропорционално.
Слика 8. Поређење таласног облика фазног напона (vL1) а напон на излазу сензора скалиран на примарни напон (vL1/Kn) током квара.
3.2. Идентификација импулса кратког споја помоћу СТМПМ
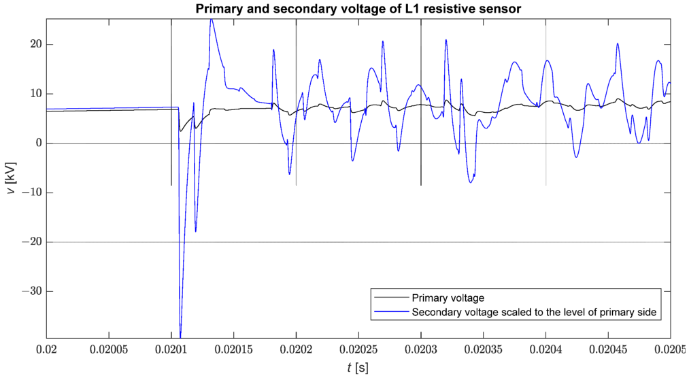
Слика 9 приказује таласни облик свих стопа опадања примера таласног облика напона у трафостаници након кратког споја трофазног нулте импедансе на земљу у чвору 816 модела. Може се видети да недостатак одабира стопа распада отежава лоцирање импулса; ово посебно важи за слабије импулсе. С друге стране, визуелно посматрање стопа опадања омогућава лаку идентификацију интервала који садрже импулсе у случају визуелне анализе таласних облика фазног напона, иако то није увек лако у случају малих амплитуда импулса.
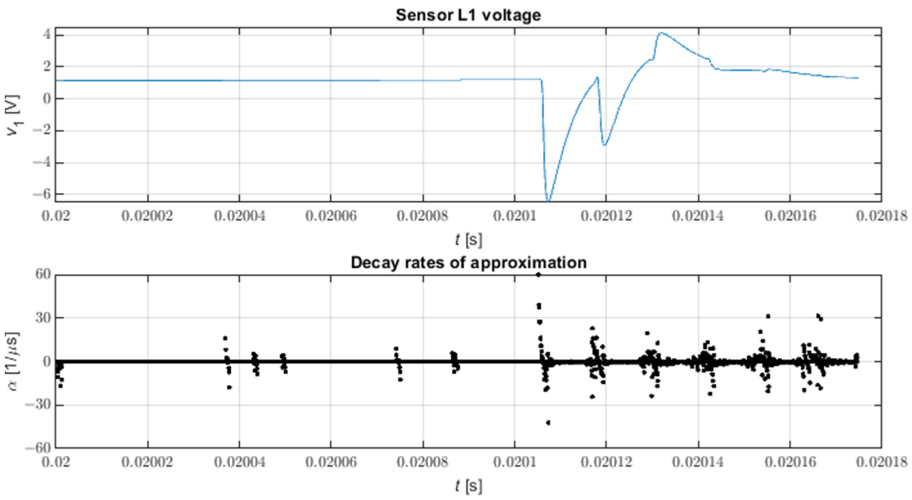
Слика 9. Све стопе распада СТМПМ апроксимације. N = 9, L = 4.
Слика 10 приказује изабране стопе опадања заједно са линеарном регресијом која се користи за идентификацију тренутка доласка импулса. Број детекција лажних импулса може се смањити филтрирањем непотребних коефицијената слабљења.
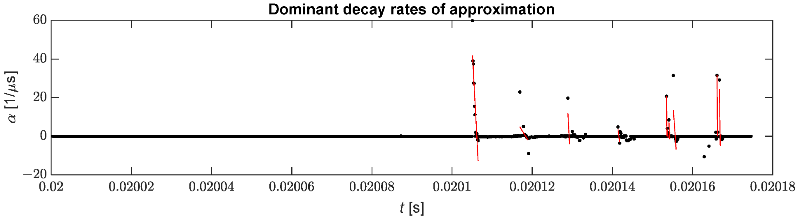
Слика 10. Одабране стопе опадања које се користе за идентификацију импулса.
У табели 2 приказане су грешке у идентификацији времена доласка првог долазног таласа на станицу. Ова грешка је дефинисана следећом једначином:
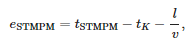
где:
- tSTMPM —тренутак доласка према СТМПМ,
- tK —тренутак грешке,
- l —удаљеност локације кратког споја од трафостанице и
- v = 299,552,300 m/s—брзина простирања таласа квара измерена за кратки спој у најудаљенијем чвору (838).
Параметри методе који се користе за добијање резултата су:
- N = 5—број узорака по временском прозору;
- L = 2—параметар оловке;
- p = 6—број тачних значајних децималних цифара мерења;
- αThr=1051s —праг детекције импулса;
- Tmax=2.1 μs —максимална ширина импулса;
- Tw=0.5 μs —ширина прозора;
- Ts=0.1 μs —период узорковања;
- r=0.02 V —праг амплитуде.
У табели 3 приказане су стандардне девијације временске грешке пулса.
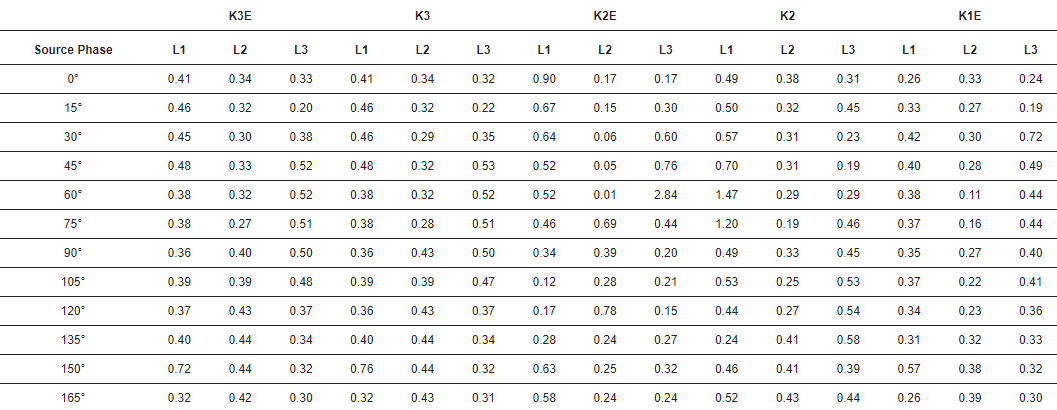
Табела 2. Временска грешка идентификације таласа у случају различитих кварова. Јединица: µс. К3Е — трофазни квар, К3 — трофазни квар, К2Е — двофазни квар, К2 — двофазни квар, К1Е — квар фаза-земља.
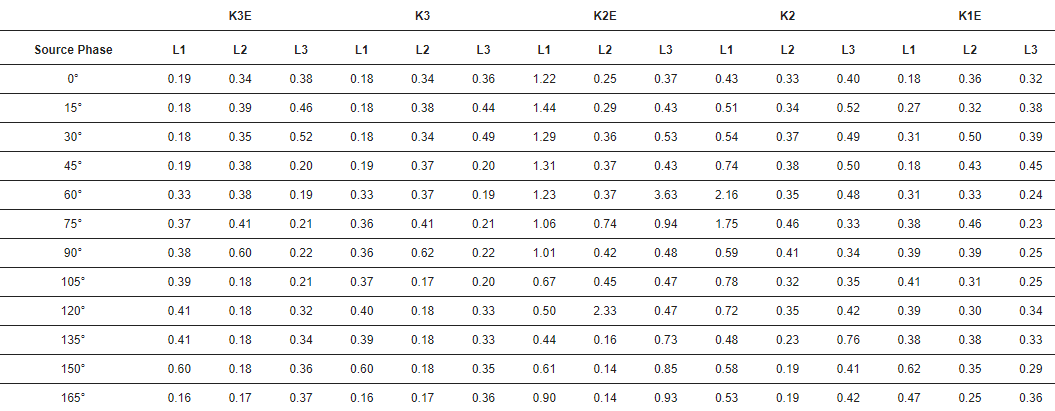
Табела 3. Стандардна девијација временске грешке. Јединица: µс. К3Е — трофазни квар, К3 — трофазни квар, К2Е — двофазни квар, К2 — двофазни квар, К1Е — квар фаза-земља.
4. Дискусија
Развијен је модел функције преноса отпорног сензора напона на основу широкопојасних мерења од 10 Хз до 20 МХз. Симулације путујућих таласа генерисаних грешком у ИЕЕЕ 34-бус моделу су изведене коришћењем функције преноса. Фреквенцијски одзив отпорног сензора био је довољан за идентификацију таласа квара у секундарном напонском сигналу. Сензор трансформише сигнале путујућих таласа са приближно константним појачањем, које је веће од појачања на корисној фреквенцији. За идентификацију је коришћен нови алгоритам у реалном времену заснован на методи матричне оловке. Варијацију ове методе која је коришћена у раду карактерише висока прецизност идентификације таласа, јер је просечна грешка била 0,41 µс при узорковању од 10 МХз, а грешка је имала позитивну вредност па је пронађено време доласка веће од стварног. Међутим, треба напоменути да се у практичним применама методе, на пример, код таласне локализације кварова, део ове грешке елиминише због диференцијалног рада ових алгоритама. Тачна идентификација таласа квара може омогућити класификацију и локализацију кварова у средњенапонским мрежама користећи сабирнице као једину мерну тачку. Потребан је тест који користи стварне сигнале да би се верификовала ефикасност алгоритма и упоредио са другим методама идентификације долазних таласних импулса. Сасвим исправна трансформација напона помоћу сензора може омогућити класификацију типа квара на основу амплитуда таласа које они генеришу.
Референце
- Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
- Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
- Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
- Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
- Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
- Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
- Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
- Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
- Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
- Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
- Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
- Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
- Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
- Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
- Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
- Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
- Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
- Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
- Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
- IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).




Leave a comment