Ідентифікація біжучих хвиль у сигналі датчика напруги в сітці середньої напруги за допомогою короткочасного методу матричного олівця

У тестах використовувався векторний аналізатор схем Omicron-Lab Bode 100, наданий DACPOL SP. Z O.O.

Анотація

Більшість методів локалізації хвилі пошкодження базуються на аналізі лінійного струму, перетвореного трансформаторами струму, і обмежуються мережами високої напруги. Локалізація хвиль пошкоджень в мережах середньої напруги ще розробляється. У цій статті представлено новий алгоритм реального часу для ідентифікації біжучих хвиль у розподільчій мережі за допомогою сигналу напруги та короткочасного методу матричного олівця. Для отримання форм сигналів напруги вторинної сторони на підстанції була розроблена модель резистивного датчика напруги на основі широкосмугових вимірювань від 10 Гц до 20 МГц. Випробуваний датчик підсилює частоти, пов’язані з біжучими хвилями, більше, ніж стандартна частота, що дозволяє ідентифікувати. Для перевірки алгоритму було виконано моделювання короткого замикання на фідері шини IEEE 34. Розроблений метод дозволяє виявляти навіть хвилі малої амплітуди.

1. Вступ

Захист енергосистеми від несправностей є однією з цілей захисного реле. Швидке усунення завад обмежує пошкодження енергетичного обладнання та зменшує його негативний вплив на якість електроенергії. Тому розробка швидких і точних реле та локаторів несправностей у розподільних мережах є ключовим питанням як з технічної, так і з економічної точки зору. У випадку мереж високої напруги локалізація несправностей проста, оскільки вони характеризуються великою дисперсією вимірювань і структурою петлі. У випадку розподільних мереж вимірювання в основному проводяться в одній точці підстанції. Крім того, розподільні мережі мають деревовидну структуру, що робить ідентифікацію несправної гілки невизначеною. Вирішенням цієї проблеми може бути використання локаторів біжучої хвилі, які в цьому випадку можуть бути більш точними, ніж звичайні методи. Щоб використання таких локаторів стало можливим, необхідно розробити найбільш точні методи ідентифікації біжучої хвилі.

Традиційний підхід до виявлення несправностей базується на аналізі струмів і напруг основної частоти. З цієї причини алгоритми захисту, засновані на цих типах сигналів, вимагають аналізу інтервалу сигналу, який є достатньо довгим, щоб переконатися, що завада сталася. Більш сучасний підхід базується на біжучих хвилях, які є сигналами вищої частоти, що поширюються вздовж ліній електропередач. Цей тип захисту іноді називають «надшвидкісним». Він виявляє хвилі струму та напруги, спричинені несправностями. Потім цей захист визначає як тип, так і розташування завад на основі порівняння їх амплітуд і часу надходження до вимірювальних пристроїв. Безперечно, ключовою перевагою хвильового захисту є швидкість спрацьовування (менше 4 мс) [1]. Крім того, він коректно працює з послідовно компенсованими лініями електропередач і під час перепадів потужності.

Визначення місця пошкодження за допомогою біжучих хвиль можна розділити на двополюсні та однополюсні схеми. У випадку двополюсних реле, збір даних вимірювань відбувається на кінцях захищених ліній і вимагає передачі даних вимірювань між пристроями. Однак однополюсні реле аналізують сигнали струмів і напруг лише з однієї точки вимірювання. Слід підкреслити, що двополюсні реле характеризуються більш високою надійністю, оскільки вони використовують хвилі, безпосередньо створені завадою, для її локалізації та класифікації. Ці хвилі мають максимально можливу амплітуду і виявляються першими після несправності. Однак у випадку однополюсних реле захист базується на хвилі, створеній завадою, і на хвилях, відбитих від розривів лінії, розгалужень і самої несправності [2]. Це через відсутність другої точки вимірювання в мережі.

Мережі високої напруги характеризуються наявністю підстанцій із вимірювальним обладнанням на кінцях лінії. Тому тут використовуються двополюсні реле. У випадку розподільних мереж підстанції високої/середньої напруги зазвичай є єдиним місцем, де розміщуються реле захисту з трансформаторами або датчиками. Це означає, що в розподільчих мережах використання односторонніх хвильових реле є найдешевшим рішенням.

Мережі розподілу – це мережі з деревовидною топологією, і ця функція ускладнює точне визначення місця пошкодження. Як для звичайних, так і для хвильових локаторів несправностей ситуація складніша, ніж у мережах передачі, оскільки на відомій відстані від підстанції може існувати кілька потенційно пошкоджених відгалужень. Пошкоджена лише одна з гілок. Однак короткозамкнену лінію можна визначити, порівнюючи амплітуди хвиль струму, розсіяних на шинах підстанцій [2,3,4].

Було запропоновано різні методи локалізації несправностей, наприклад виявлення частот, пов’язаних із хвильовими коливаннями між вузлами [5], порівняння виміряного струму з прогнозованим для заданого місця короткого замикання [6] та більш традиційні методи, засновані на виявленні хвильових фронтів розломів [3,7]. Наступні методи були використані для виявлення хвильових фронтів: вейвлет-перетворення, аналіз головних компонент на основі виділення ознак, оператор енергії Тігера, ансамблева емпірична декомпозиція моди та метод матричного олівця, який обговорюється та використовується в цій статті [8,9]. Метод матричного олівця використовується для розкладання сигналу на суму експоненціально затухаючих синусоїд [10]. У галузі електроенергетики метод матричного олівця використовувався для оцінки основних форм коливань через несправності та для оцінки гармонік і субгармонік [11,12, 13].

Електричні сигнали, оброблені за алгоритмами цифрової обробки даних, надходять на реле за допомогою вимірювальних приладів, розташованих на станції. Ці пристрої включають трансформатори струму та напруги, котушки Роговського або датчики, що знижують рівень електричних сигналів до рівня, прийнятного реле. Важливо, щоб сигнал на вторинній стороні цих пристроїв відтворювався якомога точніше, і в ідеалі його слід лише масштабувати. На практиці, однак, вимірювальні прилади мають змінний коефіцієнт посилення та зсув фази залежно від частоти сигналу. Прилад не повинен надто послаблювати високі частоти, щоб мати можливість виявити вхідну біжучу хвилю, яка є хвилею, що швидко змінюється, і тому містить високочастотні компоненти. Слід підкреслити, що для точного відтворення амплітуди хвилі несправності прилад повинен запроваджувати постійну затримку часу (бажано, щоб її не було взагалі), а його характеристики підсилення мають бути якомога менше змінними.

Трансформатори – це прилади, які традиційно використовуються в електроенергетиці для вимірювання напруги. Вони характеризуються дуже точним перетворенням електричних сигналів, але мають і недоліки. Вони сприяють негативному явищу ферорезонансу, піддаються пошкодженням, спричиненим короткими замиканнями у вторинному колі, і не здатні точно трансформувати високочастотні (>3 кГц) компоненти напруги [14]. Ось чому нетрадиційні датчики на основі механізмів, відмінних від трансформаторної системи, були розроблені як відповідь на потребу точного вимірювання перехідних компонентів [15,16].

Для вимірювання напруги датчики напруги на основі ємнісних (C), резистивних (R) і резистивно-ємнісних (RC) подільників є популярними нетрадиційними датчиками [14]. Зокрема, R та RC дільники є найпопулярнішими, оскільки вони не здатні викликати ферорезонанс через незначну індуктивність, точно трансформувати перехідні процеси та високі частоти, дозволяючи розряджатися накопиченому заряду на лінії, і стійкі до короткого замикання вторинної сторони. Ці дільники можна успішно використовувати для вимірювання якості електроенергії та визначення місця короткого замикання за допомогою хвильового явища.

Література з моделювання звичайних трансформаторів велика, але, на жаль, зазвичай посилається на опис їхніх характеристик на частотах нижче 10 кГц [15,17]. Крім того, автори не змогли знайти числові дані графіків Боде або передавальних функцій трансформаторів напруги (як звичайних, так і нетрадиційних) до 1 МГц навіть у статтях, що описують дослідження в цій галузі [18,19]. Такі дані доступні для звичайного трансформатора струму [20]. Звичайно, датчики відрізняються за конструкцією, що призводить до варіацій їхніх характеристик передачі від одного типу до іншого, але, здається, потрібно знати функцію передачі прикладу.

Для отримання таких даних були проведені вимірювання частотних характеристик датчика середньої напруги. Потім вони були використані для розробки моделі функції передачі. Потім було представлено покращений метод короткого матричного олівця для виявлення хвиль короткого замикання напруги в мережі середньої напруги, виміряних на стороні вторинної обмотки датчиків напруги.

Структура статті така. У розділі 2 наведено опис короткочасного методу матричного олівця з його застосуванням для пошуку сигнальних імпульсів. Також наведено алгоритм ідентифікації імпульсів. Розділ 3 містить результати вимірювань передатної функції датчика напруги та результати роботи алгоритму на основі проведеного моделювання. Висновки наведені в розділі 4.

2. Ідентифікація імпульсів несправності в мережі середньої напруги

2.1. Короткостроковий матричний метод олівця

Короткочасний матричний метод олівця (STMPM) апроксимує сигнал усередині вікна, який змінюється з часом, як суму синусоїдальних компонентів із експоненціально змінною амплітудою [10,21]:

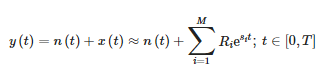
де:

• y(t) — сигнал вимірювання,
• n(t) — шум,
• x(t) — вихідний сигнал,
• Ri — залишки або комплексні амплітуди компонентів,
• Si—комплексні полюси та
• M—кількість компонентів апроксимації.

Для дискретизованого сигналу t = kT_s наведене вище рівняння має такий вигляд:

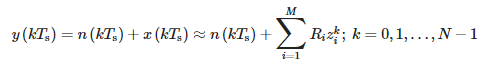
де:

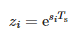
• Ts — період вибірки та
• N — кількість зразків.

Для визначення параметрів апроксимації необхідно побудувати наступну матрицю:

Тут L — це параметр олівця. Кількість компонент апроксимації M задовольняє таке співвідношення:

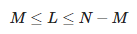
Таким чином, ми бачимо, що максимальне значення M дорівнює ⌊N/2⌋.
Піддаючи матрицю Y сингулярному розкладу (SVD), ми отримуємо:

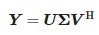
де:

• U — унітарна матриця розміром (N − L) × (N − L),
• Σ — прямокутна діагональна матриця сингулярних значень розміром (N − L) × (L + 1) і
• V — унітарна матриця розміром (L + 1) × (L + 1).

Якби виміряний сигнал не містив шуму, матриця Σ містила б точно M ненульову однину значення. Через шум одиничні значення можуть бути спотворені, що проявляється додатковими малими одиничними значеннями. Шумовий ефект усувається видаленням цих малих значень. Лише M домінантних значень, які задовольняють таку умову:

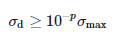
де σ_max – домінантне одиничне значення, а p – кількість точних значущих десяткових цифр вимірювання.

Потім будуються підматриці результуючих матриць SVD:

1. Матриця U′=[u1,u2,…,u_M] розміром (N − L) × M створюється шляхом залишення стовпців, що відповідають сингулярним значенням, що задовольняють умову (7), і видалення інші;
2. Квадратна діагональна матриця Σ=diag(σ1,σ2,…,σM) формується шляхом видалення стовпців і рядків матриці Σ, які містять сингулярні значення, які не задовольняють умову (7);
3. Матриця V′=[v1,v2,…,v_M] розміром (L + 1) × M формується шляхом залишення стовпців, що відповідають сингулярним значенням, які задовольняють умову (7) і видалення інших.

Тоді матриця V₁′ створюється шляхом видалення останнього рядка матриці V′. V₂′ будується шляхом видалення першого рядка матриці V′.

Потім обчислюються наступні матриці:

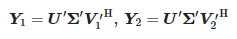
Значення zi є ненульовими узагальненими власними значеннями пари матриць (Y₁, Y₂), а саме власними значеннями Y ^†₁Y₂, де Y^†₁ є псевдооберненим Муром–Пенроузом Y₁. Потім обчислюємо полюси:

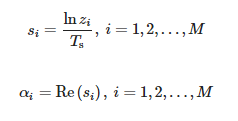
Значення амплітуд можна визначити таким чином:

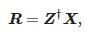
де:

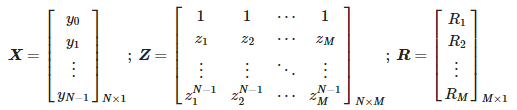
Наведені вище операції виконуються за допомогою методу олівця короткочасної матриці для послідовних інтервалів даних [9,22].

Приблизні результати власних значень, псевдоінверсій і алгоритмів SVD можуть впливати на появу ненульових значень zi, хоча й близьких до нуля. Ці значення впливають на швидкість MPM і можуть негативно вплинути на їхні результати, тому їх варто видалити перед обчисленням залишків.

2.2. Поведінка полюсів компонентів поблизу імпульсу

Несправності в електричній мережі породжують імпульси, що поширюються вздовж ліній електропередач зі швидкістю, близькою до швидкості світла [3]. Ці імпульси можна ідентифікувати за допомогою аналізу зсуву полюсів наближення STMPM. На малюнку 1 показано три приклади імпульсів гауссової форми та полюси їх апроксимації за допомогою STMPM. Коли приходить імпульс, апроксимація з експоненціальними компонентами змінюється в міру переміщення часового вікна. Коли імпульс знаходиться праворуч від середньої точки вікна, полюси апроксимації мають позитивну дійсну частину, коли вершина Гауса знаходиться в середині вікна, дійсна частина полюсів близька до нуля, а коли імпульс знаходиться в першій половині вікна полюси мають негативну дійсну частину. Таким чином, зміна знака дійсної частини полюсів вказує на те, що центр імпульсу пройшов через середню точку вікна вибірки [9,22]. На малюнку 2 ми також можемо бачити, що полюси з найбільшим абсолютним значенням дійсної частини (і, отже, з найшвидшою швидкістю зміни амплітуди) мають найбільше значення початкового модуля амплітуди (залишку).

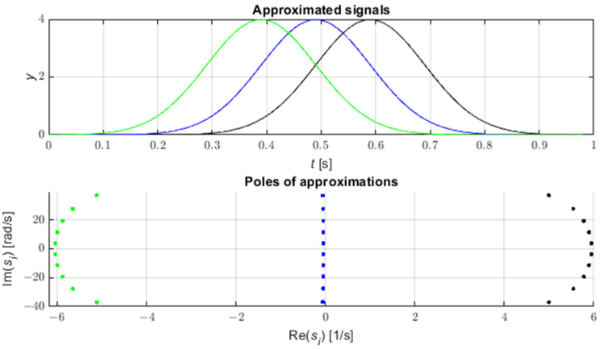
Малюнок 1. Гауссіани та відповідні полюси наближень.

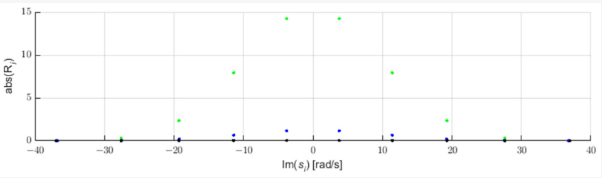
Малюнок 2. Залишки компонент гаусових наближень.

Таким чином, бачимо, що часову координату вершини імпульсу можна наближено ототожнити з моментом зміни знака коефіцієнтів загасання.

Отримавши залежний від часу хід цих коефіцієнтів за допомогою STMPM, ми можемо піддати їх лінійній апроксимації в околицях точки, де коефіцієнти проходять через нуль, і отримати приблизну верхню координату імпульсу. Слід зазначити, що коефіцієнти, які характеризуються найбільшою варіабельністю, характеризуються і найбільшою амплітудою — це найбільші складові імпульсу.

2.3. Алгоритм виявлення імпульсу в реальному часі

Блок-схема алгоритму для виявлення імпульсів, що походять від біжучих хвиль, представлена на малюнку 3. Алгоритм підпорядковує послідовні вікна сигналу STMPM, щоб виділити швидкості загасання компонентів апроксимації.

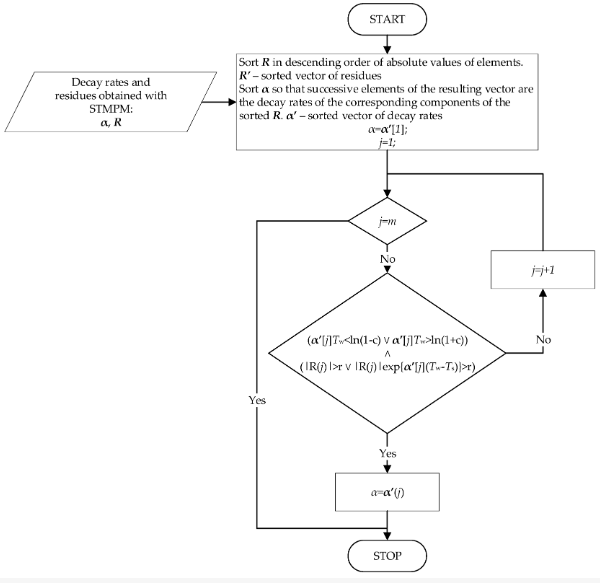
Малюнок 3. Алгоритм вибору швидкостей розпаду.

Отримані компоненти піддаються відбору, процедура якого представлена на рисунку 4. Відбір ґрунтується на припущенні, що за час піку слід приймати ті компоненти СТМПМ, які характеризуються найбільшою амплітудою. наближення — вони складають найбільший внесок у перехідну складову сигналу. Це узгоджується зі спостереженням із попереднього пункту — компоненти з найбільшою варіацією амплітуди характеризуються найбільшою початковою амплітудою. У випадку, коли компонент з найбільшою амплітудою характеризується малою швидкістю загасання протягом усього вікна довжини T_w — меншою за параметр c — або її максимальний внесок у сигнал менший за r, наступний за величиною амплітуди компонент вибирається як потенційний кандидат на швидкість розпаду α. Повторюючи цю процедуру для наступних компонентів, доки не буде виконана умова, нарешті отримуємо коефіцієнт α, який потім використовується для наближення часу приходу імпульсу. Якщо жоден із компонентів не задовольняє наведені вище умови, вибирається компонент із найвищою амплітудою.

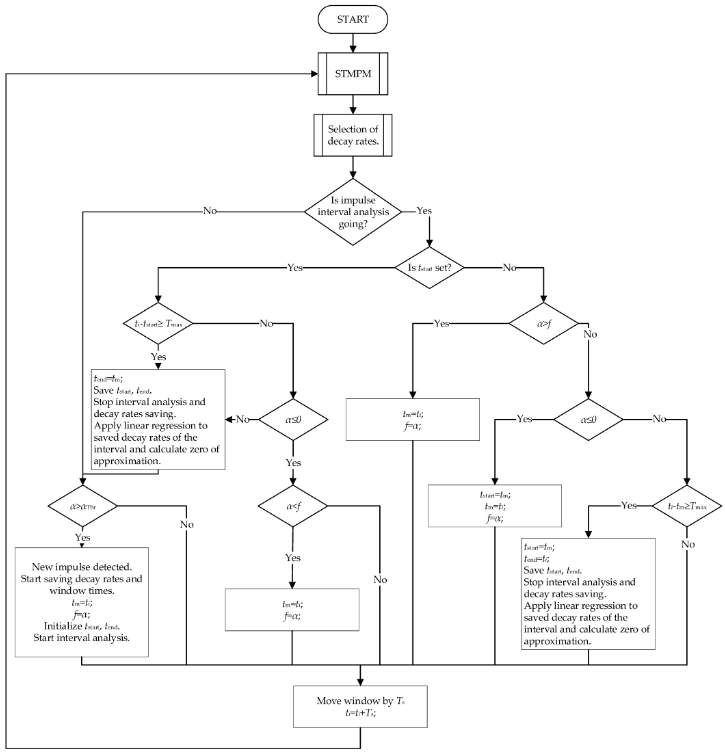
Рисунок 4. Алгоритм ідентифікації імпульсу.

Час, пов'язаний з вікном, вважається:

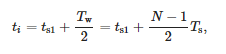
де t_s1 — час вибірки першого вікна та T_w — ширина вікна.

На надходження імпульсу вказує різке збільшення швидкості α, пов’язане зі швидкою зміною сигналу в кінці вікна вибірки. Параметр α_Thr вибрано як поріг швидкості розпаду. Коли поріг виявлення перевищено, наступні значення коефіцієнтів α та часу вікна записуються в пам’ять, і починається аналіз даних для визначення більш точних меж імпульсу. Момент t_start із найвищим значенням α перед зміною знака швидкості загасання вибирається як правильний початок імпульсу. Щоб зберегти потенційні часи правильних меж імпульсу, змінну t_m було введено зі змінною f, яка містить найбільші значення α імпульсу, обчислені на даний момент.

Якщо значення t_start знайдено, починається пошук остаточного належного кінця імпульсу t_end. Це відповідає найменшому значенню α перед тим, як знак знову зміниться, цього разу на позитивний. Змінна i_m знову використовується для збереження попередніх потенційних кінцевих точок. Змінна f містить попередні мінімальні значення α.

Коли довжина імпульсу дорівнює T_max зразків або знайдено кінець імпульсу, аналіз імпульсу припиняється.

Функція α(t) в інтервалі [t_{початок}; t_end] піддається лінійній регресії. Коефіцієнти цієї регресії знаходять як розв’язок наступної задачі:

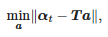
де: α_t=[α(t_{початок}),α(t_{початок}+Ts),…,α(t_end)]^T, a=[a₁,a₀]^T

Шукані коефіцієнти:

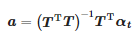
Оскільки момент приходу імпульсу:

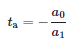
2.4. Адаптований IEEE 34-Bus Test Feeder

Для розрахунків короткого замикання в Simulink була створена тестова модель фідера IEEE з 34 шинами. Топологію фідера показано на малюнку 5 [23]. Фідер базується на реальній мережі в штаті Арізона. Це досить просто, щоб не стати значним обчислювальним тягарем під час моделювання перехідних процесів з малим кроком інтегрування. Модель було спрощено, а параметри змінено, щоб імітувати європейські сітки:

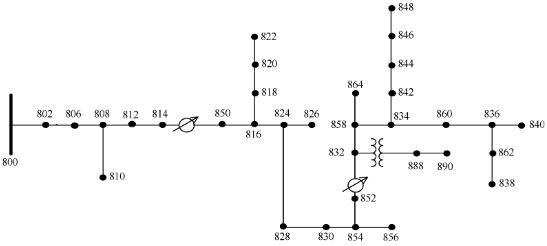
Малюнок 5. Топологія фідера IEEE 34.

• Напругу в мережі змінено з 24,9 кВ до 16,5 кВ;
• Вважалося, що всі ділянки ліній електропередач є повітряними лініями з однаковими параметрами;
• Регулятори напруги видалено;
• Передбачається, що розподілені навантаження згруповані в автобусах на дальньому кінці завантажених ліній;
• Навантаження були підключені до мережі середньої напруги через розподільні трансформатори;
• Нейтральна точка трансформатора високої/середньої напруги була від’єднана від заземлення.

Параметри джерела напруги:

• частота 50 Гц;
• Напруга в мережі 115,5 кВ;
• Опір 0,00227 Ом.
• Симетричне джерело зі зсувом фази L1, рівним 0°.

Параметри силового трансформатора:

• Коефіцієнт напруги 115,5/16,5;
• Векторна група обмотки високої напруги Yg;
• Векторна група обмотки низької напруги D11;
• Потужність 6,3 МВА;
• Відносна напруга короткого замикання 7,5%;
• Опір короткого замикання дорівнює 0,49% еквівалентного опору.

Параметри розподільних трансформаторів:

• Коефіцієнт напруги 15,75/0,4;
• Векторна група обмотки високої напруги D11;
• Векторна група обмотки низької напруги Yg;
• Потужність 630 кВА;
• Відносна напруга короткого замикання 6%;
• Опір короткого замикання дорівнює 17,2% еквівалентного опору.

Параметри ліній електропередачі:

• Трифазна лінія без нейтралі;
• Один провідник на фазу;
• Діаметр провідника 0,8466 см;
• Співвідношення T/D 0,311;
• Опір постійному струму 0,5939 Ом/км;
• Горизонтальні положення провідників x=[−1,05, 0, 1,05];
• Вертикальні положення провідників u=[−9.05, 10.61, 9.05];
• Питомий опір землі ρ=100 Ом·м.

Ємності були прикріплені до кожного трансформатора, як показано на малюнку 6 [5] в щоб змоделювати властивості трансформаторів на високих частотах.

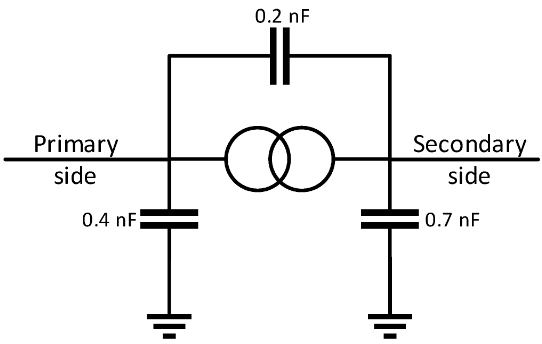
Малюнок 6. Модель трансформатора.

Лінії електропередач змодельовано в діапазоні від 1 Гц до 1 МГц з урахуванням скін-ефекту за допомогою моделі універсальної лінії.

Моделювання однофазних і багатофазних коротких замикань з опором перетину нуля проводилося при довжині ліній 20%, 50%, 80% і 100%. Він відповідає 76 місцям короткого замикання. Крок інтеграції моделювання становив Δt=0,1 мкс. Тастін/Назад Ейлер був використаним методом інтегрування.

3. Результати

3.1. Вимірювання характеристик передачі датчика середньої напруги

Вимірювання частотної характеристики проводилися для датчика середньої напруги, призначеного для монтажу в головках роз’ємів. Датчик являв собою резистивний дільник з номінальною первинною напругою 20/√3 кВ і номінальною вторинною напругою 3,25/√3, що відповідає відношенню напруг:

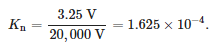
Для вимірювань використовувався векторний мережевий аналізатор Bode 100 від OMICRON Lab. Цей прилад дозволяє проводити вимірювання в діапазоні від 1 Гц до 50 МГц. Для проведення випробувань використовувалася функція вимірювання посилення та фази пристрою. Ця функція була заснована на порівнянні амплітуди і фази сигналів напруги на первинній і вторинній сторонах датчика. Вимірювання передатної функції, визначеної як відношення напруги на вторинній стороні до напруги на первинній стороні, було виконано для 2048 значень частоти в діапазоні від 10 Гц до 20 МГц. Виміряні значення представлено на малюнку 7.

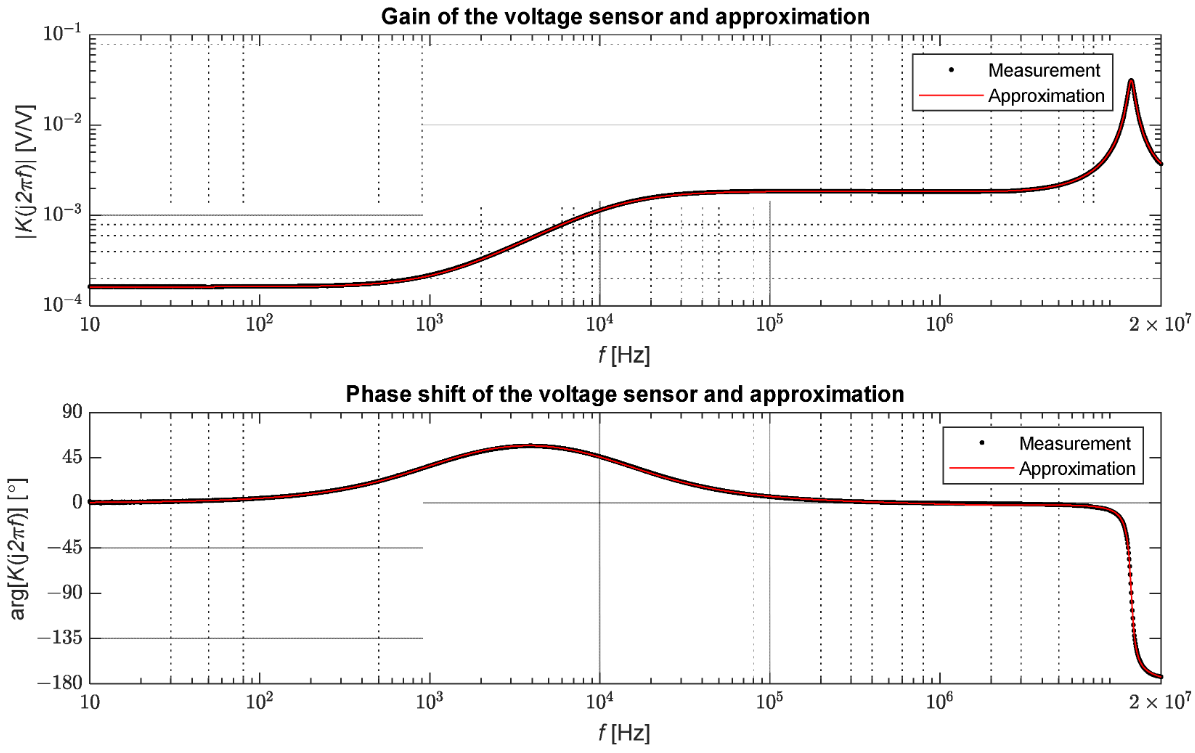
Малюнок 7. Результати вимірювання коефіцієнта пропускання датчика середньої напруги.

Випробуваний датчик напруги зберігає номінальний коефіцієнт передачі для сигналів до частоти приблизно 1 кГц, потім графік підвищується до рівня посилення приблизно 1,84 × 10⁻³; цей рівень підтримується приблизно від 12,5 кГц до 6,6 МГц. Завдяки диференціювальним властивостям датчика, тут є позитивний зсув фази приблизно на 57° в зоні переходу від 100 Гц до 100 кГц. У разі фази можна виділити дві зони, для яких зсув не перевищує 6°. У цьому випадку діапазон частот становить приблизно до 130 Гц і від 105 кГц до 9,4 МГц. Отже, можна зробити висновок, що в діапазоні від 105 кГц до 6,6 МГц сигнали пропорційно трансформуються, але з іншим коефіцієнтом пропорційності, ніж поблизу частоти мережі. У випадку хвильових явищ цього діапазону достатньо, щоб точно представити форму хвиль, що поширюються в сітці [20]. Варто зазначити, що датчики напруги з різними конструкціями можуть проявляти різні властивості передачі.

Для розробки математичної моделі датчика була використана функція «tfest» MATLAB для апроксимації отриманих даних стабільною функцією передачі наступного вигляду:

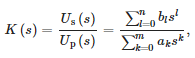
де:

• Up(s) — напруга на первинній стороні датчика,
• Us(s) — напруга на вторинній стороні датчика,
• n — порядок чисельника,
• m — порядок знаменника та
• ak, bl —коефіцієнти поліномів знаменника та чисельника пропускання, послідовно.

Значення коефіцієнтів функції передачі представлені в таблиці 1. Варто зазначити, що змодельований коефіцієнт пропускання є правильним, оскільки порядок знаменника більший за порядок чисельника. На рис. 7 також наведено порівняння передавальних функцій, отриманих із вимірювань, з апроксимацією за формулою (19). Також було розраховано середню квадратичну похибку між точками вимірювання та апроксимацію, визначену наступним співвідношенням:

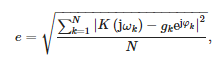
де:

• N = 2048 — кількість частот вимірювання
• g_k — виміряне посилення датчика при пульсації ω_k і
• φ_k — виміряний зсув фази датчика при пульсації ω_k.

Значення похибки апроксимації дорівнює:

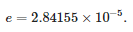
Таблиця 1. Значення поліноміальних коефіцієнтів еквівалентного пропускання датчика напруги з резистивною структурою подільника.

На малюнку 8 показано порівняння форми фазової напруги на підстанції, отриманої в результаті моделювання, і напруги на виході змодельованого датчика у випадку прямого трифазного короткого замикання на землю у вузлі 816. Це чітко видно, що посилення швидких перехідних процесів більше, ніж повільних. Варто зазначити, що ці сигнали посилюються майже пропорційно.

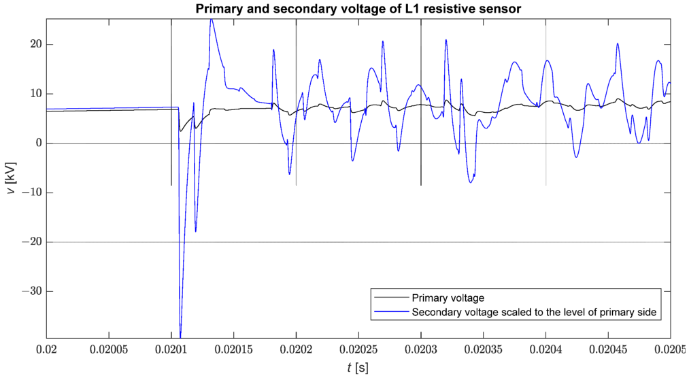
Малюнок 8. Порівняння форми фазової напруги (v_L1) і напруги на виході датчика, масштабованої до первинної напруги (v_L1/K_n) під час несправності.

3.2. Ідентифікація імпульсів короткого замикання за допомогою STMPM

На малюнку 9 показана форма сигналу всіх швидкостей спаду прикладу форми сигналу напруги на підстанції після короткого замикання трифазної мережі з нульовим опором на землю у вузлі 816 моделі. Можна побачити, що відсутність вибору швидкості загасання ускладнює визначення місцезнаходження імпульсів; це особливо вірно для слабших імпульсів. З іншого боку, візуальне спостереження за швидкостями затухання дозволяє легко ідентифікувати інтервали, що містять імпульси, у разі візуального аналізу осциллограмм фазової напруги, хоча це не завжди легко у випадку малих амплітуд імпульсів.

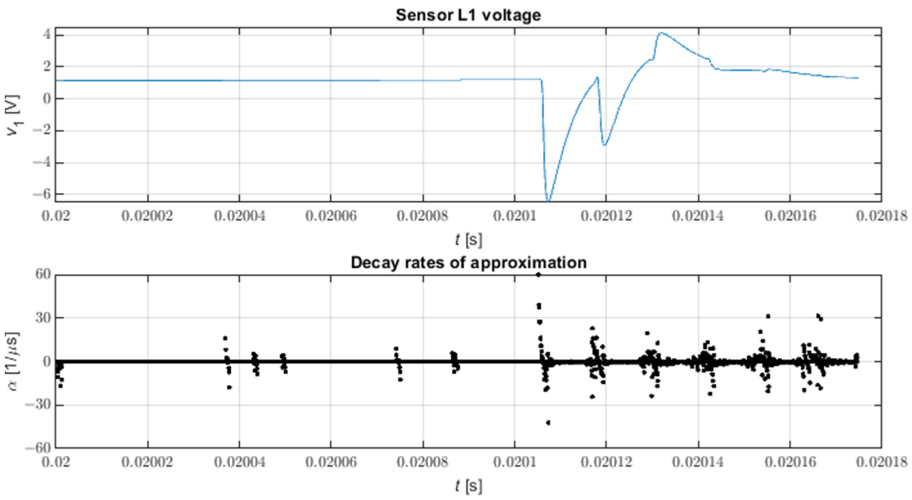
Малюнок 9. Усі швидкості загасання апроксимації STMPM. N = 9, L = 4.

На малюнку 10 показано вибрані швидкості затухання разом із лінійною регресією, яка використовується для визначення моменту надходження імпульсу. Кількість помилкових виявлень імпульсів можна зменшити, відфільтрувавши непотрібні коефіцієнти ослаблення.

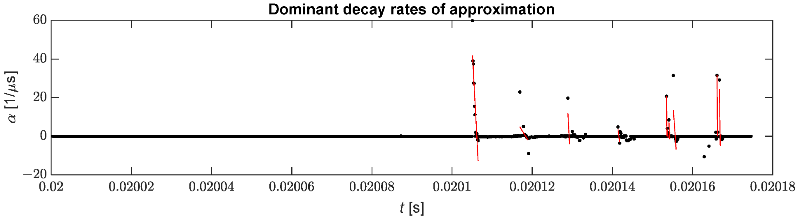
Малюнок 10. Вибрані швидкості загасання, які використовуються для ідентифікації імпульсу.

Таблиця 2 показує помилки визначення часу прибуття першої вхідної хвилі на станцію. Ця помилка визначається таким рівнянням:

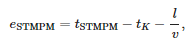
де:

• t_STPMM — момент прибуття згідно STMPM,
• t_K — момент несправності,
• l — відстань місця короткого замикання від підстанції та
• v = 299 552 300 м/с — швидкість розповсюдження хвиль розлому, виміряна для короткого замикання в найвіддаленішому вузлі (838).

Параметри методу, які використовуються для отримання результатів:

• N = 5 — кількість зразків за часове вікно;
• L = 2 — параметр олівця;
• p = 6 — кількість точних значущих десяткових цифр вимірювання;
• α_Thr=1051s — поріг виявлення імпульсу;
• T_max=2,1 мкс — максимальна ширина імпульсу;
• T_w=0,5 мкс — ширина вікна;
• T_s=0,1 мкс — період вибірки;
• r=0,02 В — поріг амплітуди.

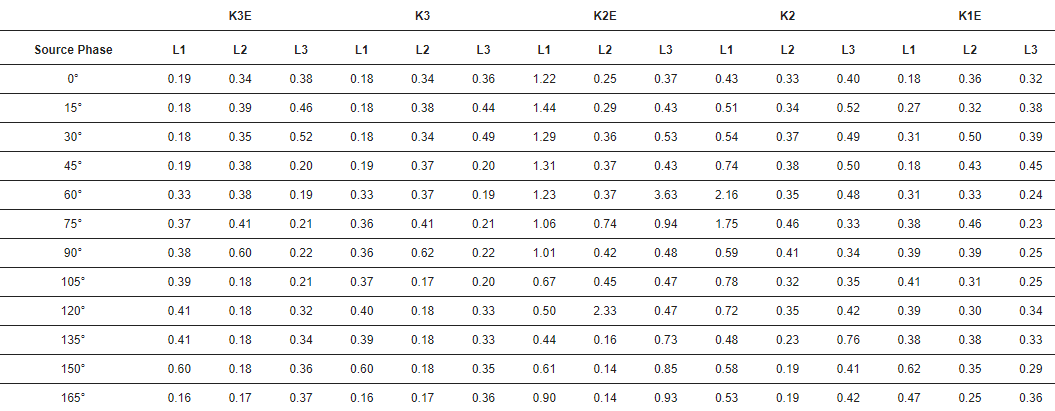
Таблиця 3 показує стандартні відхилення тимчасової похибки пульсу.

Таблиця 2. Часова похибка ідентифікації хвилі при різних розломах. Одиниця: мкс. K3E — трифазне замикання на землю, K3 — трифазне замикання, K2E — двофазне замикання на землю, K2 — двофазне замикання, K1E — фазне замикання на землю.

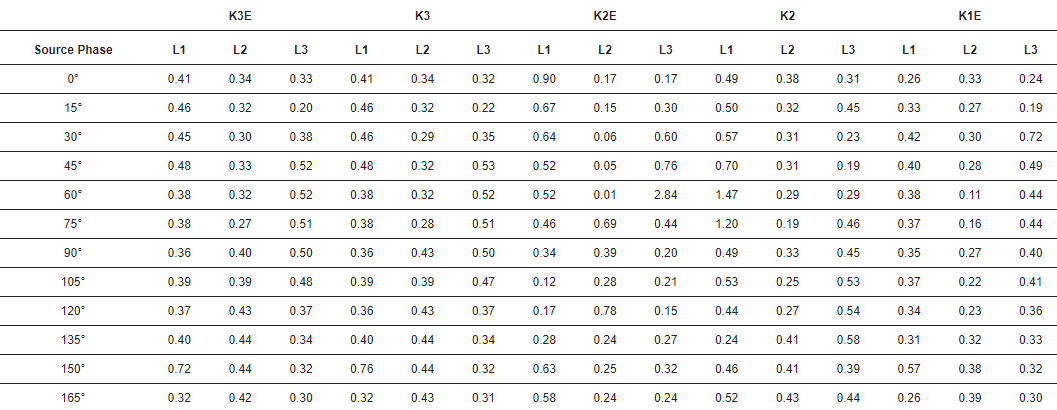
Таблиця 3. Стандартне відхилення тимчасової похибки. Одиниця: мкс. K3E — трифазне замикання на землю, K3 — трифазне замикання, K2E — двофазне замикання на землю, K2 — двофазне замикання, K1E — фазне замикання на землю.

4. Обговорення

Розроблено модель передатної функції резистивного датчика напруги на основі широкосмугових вимірювань від 10 Гц до 20 МГц. Моделювання біжучих хвиль, спричинених несправністю, у моделі шини IEEE 34 було виконано з використанням функції передачі. Частотна характеристика резистивного датчика була достатньою для ідентифікації хвиль несправності у сигналі вторинної напруги. Датчик перетворює сигнали біжучої хвилі з приблизно постійним підсиленням, яке перевищує підсилення на робочій частоті. Для ідентифікації використовувався новий алгоритм реального часу, заснований на методі матричного олівця. Використаний у роботі варіант цього методу характеризується високою точністю ідентифікації хвилі, оскільки середня похибка становила 0,41 мкс при дискретизації 10 МГц, а похибка мала позитивне значення, тому знайдений час приходу був більшим за реальний. Однак слід зазначити, що в практичних застосуваннях методу, наприклад, при хвильовій локалізації несправностей, частина цієї похибки усувається за рахунок диференціальної роботи цих алгоритмів. Точна ідентифікація хвиль несправностей може зробити можливим класифікувати та локалізувати несправності в мережах середньої напруги, використовуючи шини як єдину точку вимірювання. Щоб перевірити ефективність алгоритму та порівняти його з іншими методами ідентифікації вхідних хвильових імпульсів, необхідний тест із використанням реальних сигналів. Досить правильне перетворення напруги датчиками може дозволити класифікувати тип несправності на основі амплітуди генерованих ними хвиль.

Список літератури

1. Anderson, P.M.; Henville, C.; Rifaat, R.; Johnson, B.; Meliopoulos, S. Pilot Protection Systems. In Power System Protection, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 509–572. ISBN 978-1-119-51314-8. [Google Scholar]
2. Thomas, D.W.P.; Carvalho, R.J.O.; Pereira, E.T. Fault location in distribution systems based on traveling waves. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 242–266. [Google Scholar] [CrossRef]
3. Liu, J.G.; Dong, X.; Chen, X.; Tong, X.; Zhang, X.; Xu, S. Single Phase to Ground Fault Processing. In Fault Location and Service Restoration for Electrical Distribution Systems, 1st ed.; John Wiley & Sons: Singapore, 2016; pp. 163–203. ISBN 978-1-118-95025-8. [Google Scholar]
4. Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
5. Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-Wavelet Transform for Fault Location in Distribution Power Networks: Definition of Mother Wavelets Inferred From Fault Originated Transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
6. Hizman, H.; Crossley, P.A.; Gale, P.F.; Bryson, G. Fault section identification and location on a distribution feeder using travelling waves. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 1107–1112. [Google Scholar] [CrossRef]
7. Dwivedi, A.; Yu, X. Fault location in radial distribution lines using travelling waves and network theory. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1051–1056. [Google Scholar] [CrossRef]
8. Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Dynamic protection of power systems with high penetration of renewables: A review of the traveling wave based fault location techniques. Int. J. Electr. Power Energy Syst. 2020, 114, 105410. [Google Scholar] [CrossRef]
9. Jalilzadeh Hamidi, R.; Livani, H.; Rezaiesarlak, R. Traveling-Wave Detection Technique using Short-Time Matrix Pencil Method. IEEE Trans. Power Del. 2017, 32, 2565–2574. [Google Scholar] [CrossRef]
10. Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Trans. Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef][Green Version]
11. Crow, M.L.; Singh, A. The Matrix Pencil for Power System Modal Extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
12. Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
13. Chen, J.; Li, X.; Mohamed, M.A.; Jin, T. An Adaptive Matrix Pencil Algorithm Based-Wavelet Soft-Threshold Denoising for Analysis of Low Frequency Oscillation in Power Systems. IEEE Access 2020, 8, 7244–7255. [Google Scholar] [CrossRef]
14. Minkner, R.; Schweitzer, E.O. Low Power Voltage and Current Transducers for Protecting and Measuring Medium and High Voltage Systems. In Proceedings of the 26th Annual Western Protective Relay Conference, Spokane, WA, USA, 26–28 October 1999. [Google Scholar]
15. Schmid, J.; Kunde, K. Application of non conventional voltage and currents sensors in high voltage transmission and distribution systems. In Proceedings of the 2011 IEEE International Conference on Smart Measurements of Future Grids (SMFG), Bologna, Italy, 14–16 November 2011; pp. 64–68. [Google Scholar] [CrossRef]
16. Rahmatian, F. High-voltage current and voltage sensors for a smarter transmission grid and their use in live-line testing and calibration. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar] [CrossRef]
17. Yablokov, A.; Filatova, G.; Timofeev, A. Using of non-traditional current and voltage sensors for the fault location. In Proceedings of the Smart Grids 2017, Tomsk, Russia, 9–13 October 2017. [Google Scholar] [CrossRef][Green Version]
18. Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. [Google Scholar] [CrossRef] [PubMed]
19. Crotti, G.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M. Medium Voltage Divider Coupled with an Analog Optical Transmission System. IEEE Trans. Instrum. Meas. 2014, 63, 2349–2357. [Google Scholar] [CrossRef]
20. Elhaffar, A.; Lehtonen, M. High Frequency Current Transformer Modeling for Traveling Waves Detection. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
21. Sarkar, T.K.; Salazar-Palma, M.; Zhu, M.D.; Chen, H. Modern Characterization of Electromagnetic Systems and Its Associated Metrology, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 21–106. ISBN 978-1-119-07646-9. [Google Scholar]
22. Rezaiesarlak, R.; Manteghi, M. Short-Time Matrix Pencil Method for Chipless RFID Detection Applications. IEEE Trans. Antennas Propag. 2013, 61, 2801–2806. [Google Scholar] [CrossRef]
23. IEEE Power Engineering Society Power System Analysis, IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 27 April 2022).

Стаття за: Piotr Łukaszewski, Łukasz Nogal*, Artur Łukaszewski

Institute of Electrical Power Engineering, Warsaw University of Technology, 75 Koszykowa St., 00-662 Warsaw, Poland; [email protected] (P.Ł.); [email protected] (Ł.N.); [email protected] (A.Ł.)
*Author to whom correspondence should be addressed.
Academic Editor: Surender Reddy Salkuti
Energies 2022, 15(12), 4307; https://doi.org/10.3390/en15124307
Received: 24 May 2022 / Revised: 9 June 2022 / Accepted: 10 June 2022 / Published: 12 June 2022
(This article belongs to the Section F1: Electrical Power System)

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).